Class 8 Maths Chapter 8 Question Answers - Algebraic Expressions and Identities
Q1: Write two examples of each of:
(i) Monomials
(ii) Binomials
(iii) Trinomials
Ans:
(i) Monomials:
(a) 7x
(b) -62xy²
(ii) Binomials:
(a) 4p + q
(b) -75a + 42b
(iii) Trinomials:
(a) a + b + c
(b) x² - 45x + 2
Q2: Add the following :
(a) 9x2−6x+7 and 5x2+4x−3.
(b) 7x2+3x−5 and 4x2−2x+6.
Ans:
(a)  The sum is 14x2−2x+4.
The sum is 14x2−2x+4.
(b)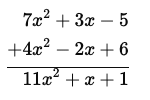 The sum is 11x2+x+1.
The sum is 11x2+x+1.
Q2: Multiply (6x2 – 5x + 3) by (3x2 + 7x – 3)
Ans: (6x2 – 5x + 3) × (3x2 + 7x – 3)
= 6x2(3x2 + 7x – 3) – 5x(3x2 + 7x – 3) + 3(3x2 + 7x – 3)
= 18x4 + 42x3 – 18x2 – 15x3 – 35x2 + 15x + 9x2 + 21x – 9
= 18x4 + 42x3 – 15x3 – 18x2 – 35x2 + 9x2 + 15x + 21x – 9
= 18x4 + 27x3 – 44x2 + 36x – 9
Q3: Multiply (3x2 + 5y2) by (5x2 – 3y2)
Ans: (3x2 + 5y2) × (5x2 – 3y2)
= 3x2(5x2 – 3y2) + 5y2(5x2 – 3y2)
= 15x4 – 9x2y2 + 25x2y2 – 15y4
= 15x4 + 16x2y2 – 15y4
Q4: Subtract the following :
(a) 4x4−3x3+5x2−2x+7 from 5x4−6x3+4x2−x+9.
(b) 3x5−4x4+6x3−2x2+x−5 from 5x5−3x4+2x3−x2+4x+7.
Ans:
(a) 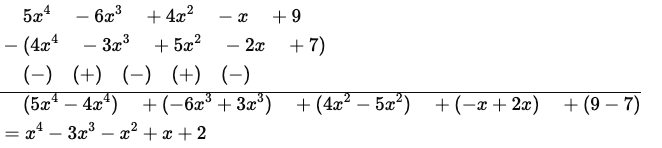 (b)
(b) 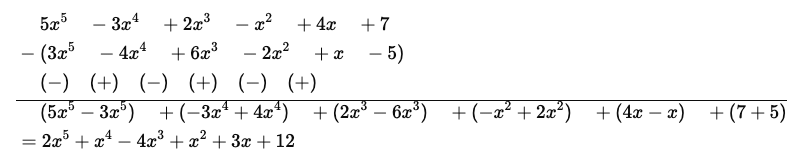
Q5: Find the product of the following pairs of monomials.
(i) 3x,5y
(ii) −6x,2x2
(iii) −7x,−3x3
(iv) 4xy,−2y2
(v) 5x2y,0
Ans:
3x × 5y = (3 × 5)×(x × y) = 15xy
(ii)−6x × 2x2 = (−6 × 2) × (x × x2) = −12x3
(iii) −7x × −3 x 3 = (−7 × −3) × (x × x3) = 21x4
(iv) 4xy × −2y2 = (4 × −2) × (xy × y2) = −8xy3
(v) 5x2y × 0 = 5 × x2y × 0 = 0
Q6: Simplify: 2x2(x + 2) – 3x (x2 – 3) – 5x(x + 5)
Ans: 2x2(x + 2) – 3x(x2 – 3) – 5x(x + 5)
= 2x3 + 4x2 – 3x3 + 9x – 5x2 – 25x
= 2x3 – 3x3 – 5x2 + 4x2 + 9x – 25x
= -x3 – x2 – 16x
Q7: Simplify the following :
(i) (y2−4) (y + 3) + 12
(ii) (m2+6)(n3−2)+7
Ans: (i) Simplifying (y2−4) (y + 3) + 12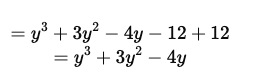 (ii) Simplifying (m2+6)(n3−2)+7
(ii) Simplifying (m2+6)(n3−2)+7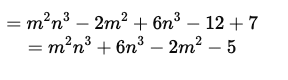 Q8: Identify the like expressions:
Q8: Identify the like expressions:
7a, −2a, 4b2, −6b2, ab, −3ab
Ans: Like terms:
- 7a and −2a
- 4b2 and −6b2
- ab and −3ab
Q9: Find the area of the rectangle whose length and breadth are 4x2y m and7xy3 m respectively.
Ans: 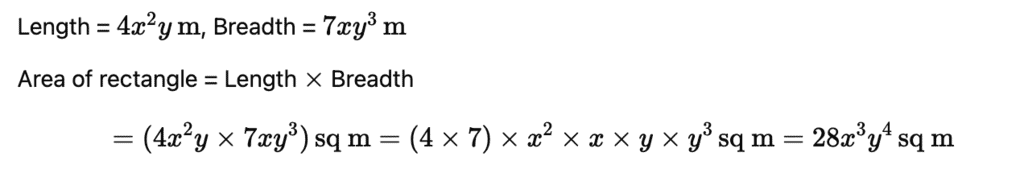
Q10. The cost of painting a rectangular board is calculated based on its area. If the length of the board is 5x3y2 m and the breadth is3xy3 m, find the area of the board to estimate the cost of painting.
Ans: 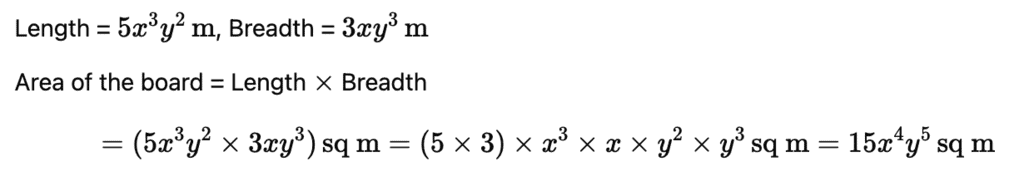
|
81 videos|423 docs|31 tests
|
















