Polynomials Class 10 Notes Maths Chapter 2
| Table of contents |

|
| What are Polynomials? |

|
| Degree of a Polynomial |

|
| Zeros of Polynomial |

|
| Relationships between Zeros and Coefficient of Polynomials |

|
What are Polynomials?
- “Polynomial” comes from the word ‘Poly’ (Meaning Many) and ‘nomial’ (in this case meaning Term) so it means many terms.
- A polynomial is made up of terms that are only added, subtracted or multiplied.
- A quadratic polynomial in x with real coefficients is of the form ax2 + bx + c, where a, b, c are real numbers with a ≠ 0.
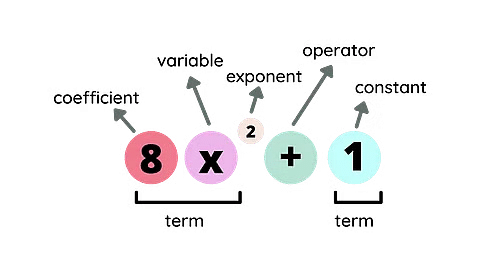
Degree of a Polynomial
- Degree: The highest exponent of the variable in the polynomial is called the degree of polynomial. For Example: 3x3 + 4, here degree = 3.
- Polynomials of degrees 1, 2 and 3 are called linear, quadratic and cubic polynomial respectively.
- A polynomial can have terms which have Constants like 3, -20, etc., Variables like x and y and Exponents like 2 in y2.
- These can be combined using addition, subtraction and multiplication but not division.
Zeros of Polynomial
The zeroes of a polynomial p(x) are precisely the x-coordinates of the points, where the graph of y = p(x) intersects the x-axis.
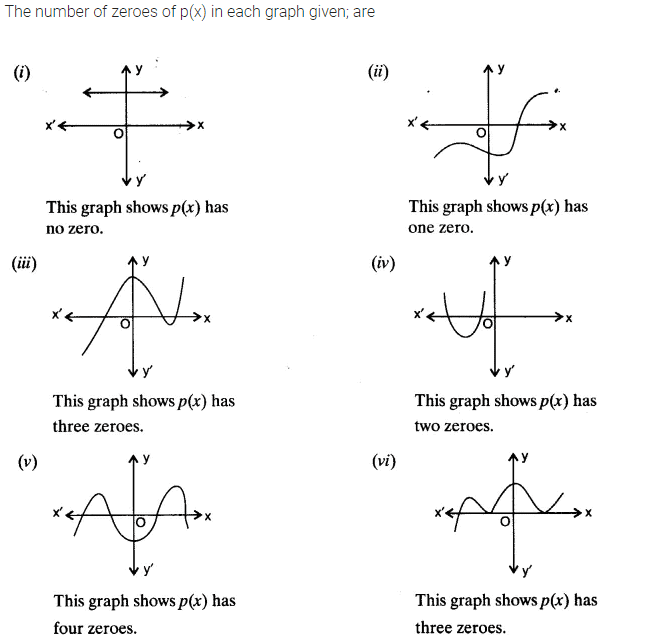
For example:
Let's consider the polynomial f(x) = x2 - 4.
- The zeros of this polynomial are the x-values where f(x) = 0.
- So we have to solve the equation x2 - 4 = 0.
- This can be factored to (x - 2)(x + 2) = 0.
- Setting each factor equal to zero gives us the solutions x = 2 and x = -2.
- So, the zeros of the polynomial x2 - 4 are 2 and -2. That means when we substitute these values into the polynomial, the result will be zero.
Relationships between Zeros and Coefficient of Polynomials
1. Linear Polynomial
The linear polynomial is an expression, in which the degree of the polynomial is 1. The linear polynomial should be in the form of ax+b. Here, “x” is a variable, “a” and “b” are constant.
The polynomial P(x) is ax+b, then the zero of a polynomial is -b/a = – constant term/coefficient of x
For Example: P(x)=2x+4
Coefficient of x (i.e., "a") is 2. Constant Term is 4.
The zero is given by:
x = - constant term/ coefficient of x = - 4/2 = -2
Thus, the zero pf P(x)= 2x + 4 is x = -2. This can be verifies by substituting x = -2 into the polynomial:
P(-2) = 2(-2) + 4 = -4 + 4 = 0
So, x = -2 is the zero of the polynomial P(x)= 2x + 4.
2. Quadratic Polynomial
The Quadratic polynomial is defined as a polynomial with the highest degree of 2. The quadratic polynomial should be in the form of ax2 + bx + c. In this case, a ≠ 0. Let say α and β are the two zeros of a polynomial, then
The sum of zeros, α + β is -b/a = – Coefficient of x/ Coefficient of x2
The product of zeros, αβ is c/a = Constant term / Coefficient of x2
For Example: Evaluate the sum and product of zeros of the quadratic polynomial 4x2 – 9.
Solution: Given quadratic polynomial is 4x2 – 9.
4x2 – 9 can be written as 2x2 – 33, which is equal to (2x+3)(2x-3).
To find the zeros of a polynomial, equate the above expression to 0
(2x+3)(2x-3) = 0
2x+3 = 0
2x = -3
x = -3/2
Similarly, 2x-3 = 0,
2x = 3
x = 3/2
Therefore, the zeros of a given quadratic polynomial is 3/2 and -3/2.
Finding the sum and product of a polynomial:
The sum of the zeros = (3/2)+ (-3/2) = (3/2)-(3/2) = 0
The product of zeros = (3/2).(-3/2) = -9/4.
3. Cubic Polynomial
The cubic polynomial is a polynomial with the highest degree of 3. The cubic polynomial should be in the form of ax3 + bx2 + cx + d, where a ≠ 0. Let say α, β, and γ are the three zeros of a polynomial, then
The sum of zeros, α + β + γ is -b/a = – Coefficient of x2/ coefficient of x3
The sum of the product of zeros, αβ+ βγ + αγ is c/a = Coefficient of x/Coefficient of x3
The product of zeros, αβγ is -d/a = – Constant term/Coefficient of x3
For Example: Find the sum of the roots and the product of the roots of the polynomial x3 -2x2 – x + 2.
Solution: Given Polynomial, x3 -2x2 – x + 2comparing with ax3 + bx2 + cx + d = 0
a = 1, b= -2, c = -1, and d = 2
Sum of the roots (p + q+ r) = – Coefficient of x2/ coefficient of x3
= -b/a
= -(-2)/1 = 2Product of the roots (pqr) = – Constant Term/Coefficient of x3
= -d/a
= -2/1 = -2
|
127 videos|584 docs|79 tests
|
FAQs on Polynomials Class 10 Notes Maths Chapter 2
| 1. What are polynomials and how are they defined? |  |
| 2. How is the degree of a polynomial determined? |  |
| 3. What are zeros of a polynomial and how are they related to the polynomial's factors? |  |
| 4. How can we find the relationship between the zeros and coefficients of a polynomial? |  |
| 5. What is the Division Algorithm for polynomials and how is it used? |  |
















