Lines and Angles Class 9 Notes Maths Chapter 6
Basic Terms and Definitions
- Point: A Point is that which has no component. It is represented by a dot.
- Line: When we join two distinct points then we get a line. A line has no endpoints it can be extended infinitely.
- Line Segment: It is the part of the line which has two endpoints.
- Ray: Ray is also a part of the line which has only one endpoint and has no end on the other side.
Term | Dimensions | Graphic | Symbol |
| Point | Zero |  | 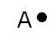 |
| Line Segment | One | 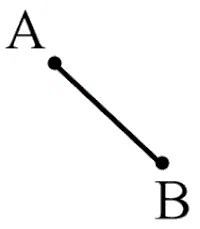 | 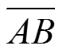 |
| Ray | One |  |  |
| Line | One |  | 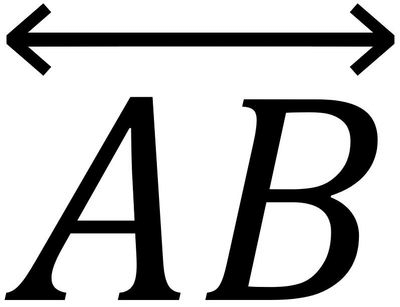 |
- Collinear and Non-collinear points: Points lie on the same line are known as collinear points and the points that don't lie on the same line are known as Non-Collinear Points.
 Collinear and Non-collinear points
Collinear and Non-collinear points
Angles
When two rays begin from the same endpoint then they form an Angle. The two rays are the arms of the angle and the endpoint is the vertex of the angle.
Types of Angles
Complementary and Supplementary Angles
- Complementary Angles are those which have the sum of two angles as 90°.
- Supplementary Angles are those which have the sum of two angles as 180°.
Relation between two Angles

Intersecting Lines and Non-intersecting Lines
There are two ways to draw two lines-
1. The lines which cross each other from a particular point is called Intersecting Lines.
2. The lines which never cross each other at any point are called Non-intersecting Lines. These lines are called Parallel Lines and the common length between two lines is the distance between parallel lines.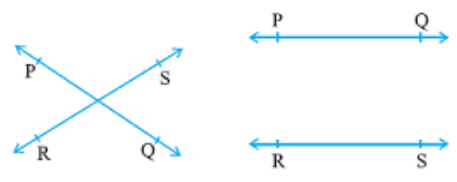
Pairs of Angles Axioms
1. If a ray stands on a line, then the sum of two adjacent angles formed by that ray is 180°.
This shows that the common arm of the two angles is the ray which is standing on a line and the two adjacent angles are the linear pair of the angles. As the sum of two angles is 180° so these are supplementary angles too.
2. If the sum of two adjacent angles is 180°, then the arms which are not common of the angles form a line.
This is the reverse of the first axiom which says that the opposite is also true.
Vertically Opposite Angles Theorem
When two lines intersect each other, then the vertically opposite angles so formed will be equal.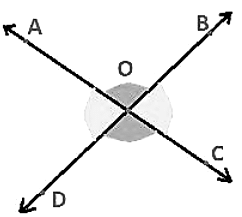
AC and BD are intersecting each other so ∠AOD = ∠BOC and ∠AOB = DOC.
Parallel Lines and a Transversal
If a line passes through two distinct lines and intersects them at distant points then this line is called Transversal Line.
Here line “l” is transversal of line m and n.
Exterior Angles - ∠1, ∠2, ∠7 and ∠8
Interior Angles - ∠3, ∠4, ∠5 and ∠6
Pairs of angles formed when a transversal intersects two lines-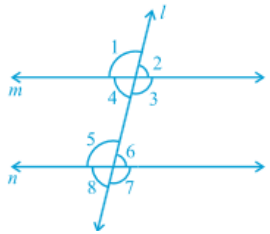
1. Corresponding Angles :
- ∠ 1 and ∠ 5
- ∠ 2 and ∠ 6
- ∠ 4 and ∠ 8
- ∠ 3 and ∠ 7
2. Alternate Interior Angles :
- ∠ 4 and ∠ 6
- ∠ 3 and ∠ 5
3. Alternate Exterior Angles:
- ∠ 1 and ∠ 7
- ∠ 2 and ∠ 8
4. Interior Angles on the same side of the transversal:
- ∠ 4 and ∠ 5
- ∠ 3 and ∠ 6
Transversal Axioms
1. If a transversal intersects two parallel lines, then
- Each pair of corresponding angles will be equal.
- Each pair of alternate interior angles will be equal.
- Each pair of interior angles on the same side of the transversal will be supplementary.
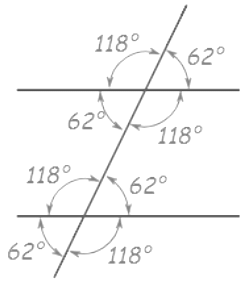
2. If a transversal intersects two lines in such a way that
- Corresponding angles are equal then these two lines will be parallel to each other.
- Alternate interior angles are equal then the two lines will be parallel.
- Interior angles on the same side of the transversal are supplementary then the two lines will be parallel.
Example: Find ∠DGH.
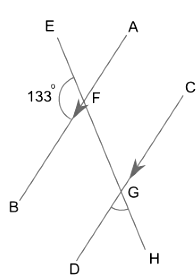
Sol:
Here, AB ∥ CD and EH is transversal.
∠EFB + ∠BFG = 180° (Linear pair)
∠BFG = 180°- 133°
∠BFG = 47°
∠BFG =∠DGH (Corresponding Angles)
∠DGH = 47°
Lines Parallel to the Same Line

If two lines are parallel with a common line then these two lines will also be parallel to each other.
As in the above figure if AB ∥ CD and EF ∥ CD then AB ∥ EF.
Angle Sum Property of a Triangle
1. The sum of the angles of a triangle is 180º.
∠A + ∠B + ∠C = 180°
2. If we produce any side of a triangle, then the exterior angle formed is equal to the sum of the two interior opposite angles.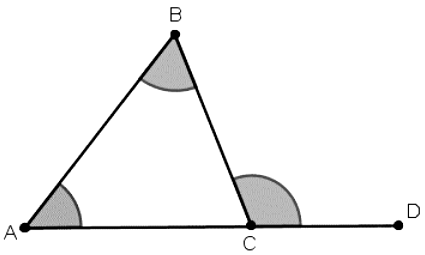
∠BCD = ∠BAC + ∠ABC
Example: Find x and y.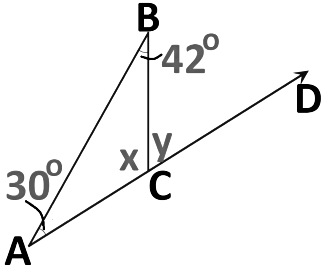
Sol:
Here, ∠A + ∠B + ∠C = 180° (Angle sum property)
30°+ 42° + x = 180°
x = 180° - (30° + 42°)
x = 108°
And y is the exterior angle and the two opposite angles are ∠A and ∠B.
So,
∠BCD = ∠A + ∠B (Exterior angle is equal to the sum of the two interior opposite angles).
y = 30°+ 42°
y = 72°
We can also find it by linear pair axiom as BC is a ray on the line AD, so
x + y = 180° (linear pair)
|
40 videos|563 docs|57 tests
|






















