Heron’s Formula Class 9 Notes Maths Chapter 10
Heron’s Formula Perimeter
It is the outside boundary of any closed shape. To find the perimeter we need to add all the sides of the given shape.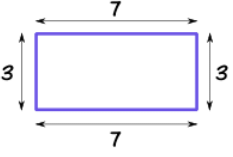
The perimeter of a rectangle is the sum of its all sides. Its unit is same as of its length.
Perimeter = 3 + 7 + 3 + 7 cm
Perimeter of rectangle = 20 cm
Area
Area of any closed figure is the surface enclosed by the perimeter. Its unit is square of the unit of the length.
Area of a triangle
The general formula to find the area of a triangle, if the height is given, is
Area of a Right Angled Triangle
If we have to find the area of a right-angled triangle then we can use the above formula directly by taking the two sides having the right angle one as the base and one as height.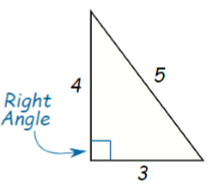
Here base = 3 cm and height = 4 cm
Area of triangle = 1/2 × 3 × 4
= 6 cm2
Remark: If you take base as 4 cm and height as 3 cm then also the area of the triangle will remain the same.
Area of Equilateral Triangle
If all the three sides are equal then it is said to be an equilateral triangle. In the equilateral triangle, first, we need to find the height by making the median of the triangle.
Here the equilateral triangle has three equal sides i.e. 10 cm.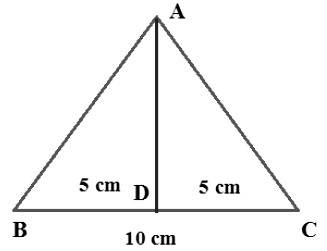
If we take the midpoint of BC then it will divide the triangle into two right angle triangle.
Now we can use the Pythagoras theorem to find the height of the triangle.
AB2 = AD2 + BD2
(10)2 = AD2 + (5)2
AD2 = (10)2 – (5)2
AD2 = 100 - 25 = 75
AD = 5√3
Now we can find the area of triangle by
Area of triangle = 1/2 × base × height
= 1/2 × 10 × 5√3
25√3 cm2
Area of Isosceles Triangle
In the isosceles triangle also we need to find the height of the triangle then calculate the area of the triangle.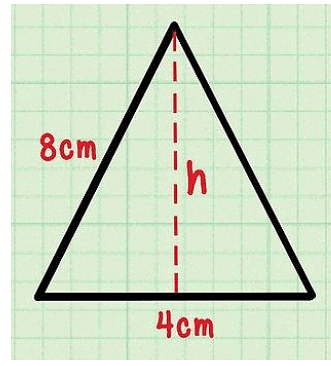
Here,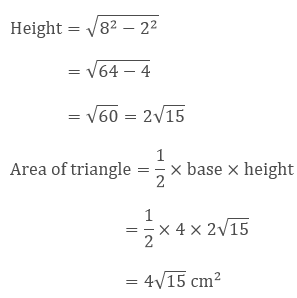
Area of a Triangle — by Heron’s Formula
The formula of area of a triangle is given by heron and it is also called Hero’s Formula.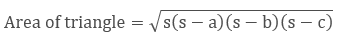
where a, b and c are the sides of the triangle and s is the semiperimeter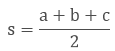
Generally, this formula is used when the height of the triangle is not possible to find or you can say if the triangle is a scalene triangle.
Here the sides of triangle are
AB = 12 cm
BC = 14 cm
AC = 6 cm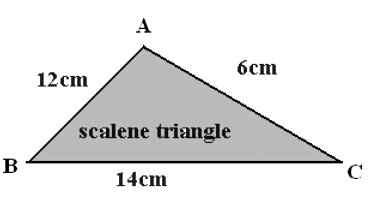

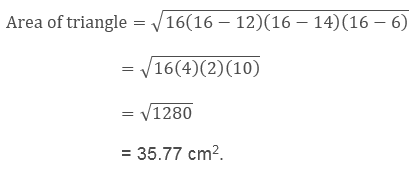
Application of Heron’s Formula in Finding Areas of Quadrilaterals
If we know the sides and one diagonal of the quadrilateral then we can find its area by using the Heron's formula.
Find the area of the quadrilateral if its sides and the diagonal are given as follows.
Given, the sides of the quadrilateral
AB = 9 cm
BC = 40 cm
DC = 28 cm
AD = 15 cm
Diagonal is AC = 41 cm
Here, ∆ABC is a right angle triangle, so its area will be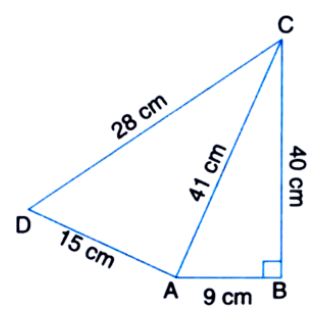
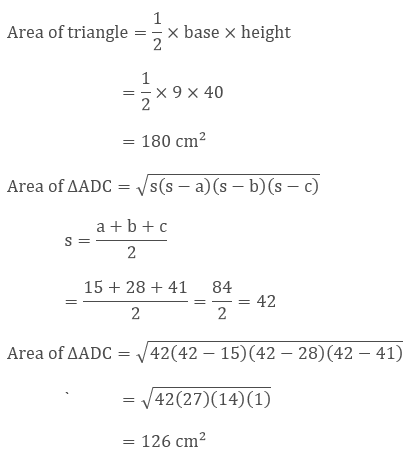
Area of Quadrilateral ABCD = Area of ∆ABC + Area of ∆ADC
= 180 cm2 + 126 cm2
= 306 cm2
|
40 videos|471 docs|57 tests
|
















