Knowing our Numbers Class 6 Notes Maths Chapter 1
Comparing Numbers
1. Compare 4978 and 5643…….
5643 is greater as the digit at the thousands place in 5643 is greater than that in 4978.
2. Compare 9364, 8695, 8402 and 7924
9364 is the greatest as it has the greatest digit at the thousands place in all the numbers.
Whereas 7924 is the smallest as it has the smallest digit at the thousands place in all the numbers.
3. Compare 56321 and 56843
Here, we will start by checking the thousands place.As the digit 5 at ten thousand place is same so we will move forward and see the thousands place. The digit 6 is also same so we will still move on further to check the hundreds place.
The digit at the hundreds place in 56843 is greater than that in 56321
Thus 56843 is greater than 56321
Proper Order
- If we arrange the numbers from the smallest to the greatest then it is said to be an Ascending order.
- If we arrange the numbers from the greatest to the smallest then it is said to be Descending order.
Example: Arrange the following heights in ascending and descending order.
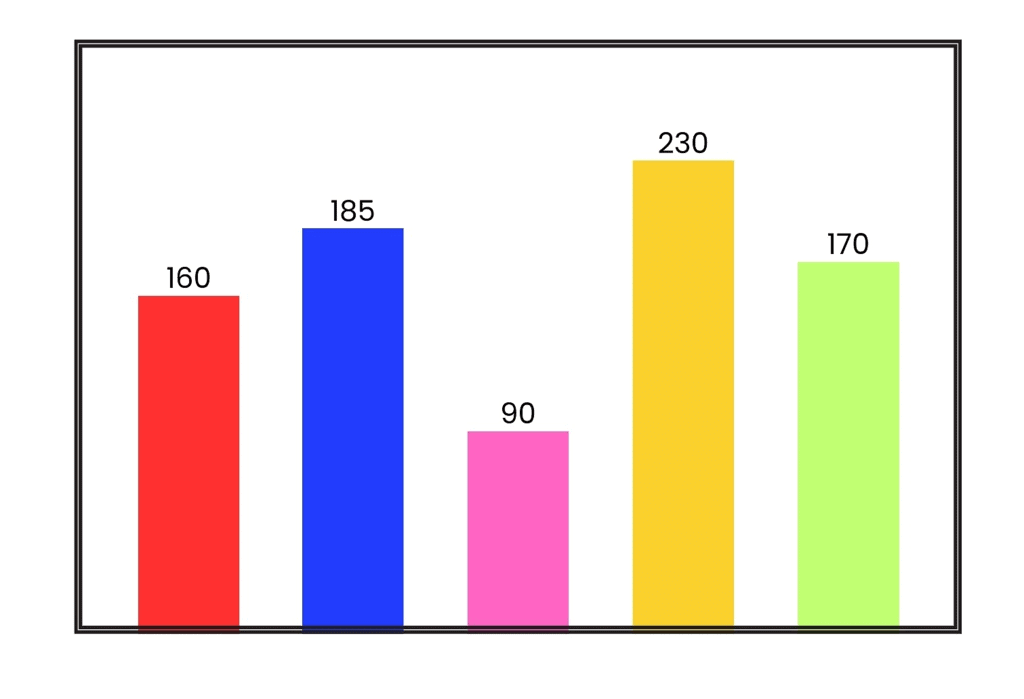
Sol:
Ascending order – 90 < 160 < 170 < 185 < 230
Descending order – 230 >185 >170 > 160 > 90
Shifting Digits
Let us understand the number formation with the help oof an example.
Example:
Form the largest and the smallest possible numbers using 3,8,1,5 without repetition
Largest number will be formed by arranging the given numbers in descending order – 8531
The smallest number will be formed by arranging the given numbers in ascending order – 1358
Introducing 10,000
99 is the greatest 2-digit number
999 is the greatest 3-digit number
9999 is the greatest 4-digit number
Observation
- If we add 1 to the greatest single digit number then we get the smallest 2-digit number
(9 + 1 = 10) - If we add 1 to the greatest 2- digit number then we get the smallest 3-digit number
(99 + 1 = 100) - If we add 1 to the greatest 3- digit number then we get the smallest 4-digit number
(999 + 1 = 1000)
Moving forward, all the above situations are same as adding 1 to the greatest 4-digit number is the same as the smallest 5-digit number. (9999 + 1 = 10,000), and it is known as ten thousand.
As above pattern if we add 1 to the greatest 5-digit number then we will get the smallest 6-digit number
(99,999 + 1 = 1,00,000)
This number is called one lakh.
Place Value
It refers to the positional notation which defines a digits position.
For Example: 6931 Here, 1 is at one's place, 3 is at tens place, 9 is at hundreds place and 6 is at thousands place
Expanded form
It refers to expand the number to see the value of each digit.
For Example:
6821 = 6000 + 800 + 20 + 1
= 6 × 1000 + 8 × 100 + 2 × 10 + 1×1
Introducing 1,00,000
Introducing 1,00,000
- The greatest 5-digit number is 99,999.
- If we add 1 to the greatest 5-digit number, we obtain the smallest 6-digit number: 99,999 + 1 = 1,00,000.
- This newly formed number is known as "one lakh," and it is the next number after 99,999.
- The relationship between 99,999 and 1,00,000 is represented mathematically as 10 × 10,000 = 1,00,000.
Observations:
1. Addition Pattern:
- Adding 1 to the greatest 5-digit number yields the smallest 6-digit number: 99,999 + 1 = 1,00,000.
- Extending the pattern, if we add 1 to the greatest 6-digit number, we will get the smallest 7-digit number: 999,999 + 1 = 10,00,000, known as "ten lakh."
2. Expanded Form of 6-digit Numbers:
- We can express 6-digit numbers in the expanded form, illustrating the place value of each digit: 2,46,853 = 2 × 1,00,000 + 4 × 10,000 + 6 × 1,000 + 8 × 100 + 5 × 10 + 3 × 1.
- The number 2,46,853 is read as "two lakh forty-six thousand eight hundred fifty-three," indicating the values at each place: 2 at the lakh place, 4 at the ten thousand places, 6 at the thousand places, 8 at the hundred places, 5 at the ten places, and 3 at the ones place.
Larger Numbers
To get the larger numbers also, we will follow the same pattern. We will get the smallest 7-digit number if we add one more to the greatest 6-digit number, which is called Ten Lakh. Going forward if we add 1 to the greatest 7-digit number then we will get the smallest 8-digit number which is called One Crore.
Remark:
1 hundred = 10 tens
1 thousand = 10 hundreds = 100 tens
1 lakh = 100 thousands = 1000 hundreds
1 crore = 100 lakhs = 10,000 thousands
Pattern
9 + 1 = 10
99 + 1 = 100
999 + 1 = 1000
9,999 + 1 = 10,000
99,999 + 1 =1,00,000
9,99,999 + 1 = 10,00,000
99,99,999 + 1 = 1,00,00,000
Reading and Writing Large Numbers
We can identify the digits in ones place, tens place and hundreds place in a number by writing them under the tables O, T and H.
AS:
Use of Commas
We use commas in large numbers to ease reading and writing. In our Indian System of Numeration, we use ones, tens, hundreds, thousands and then lakhs and crores.
We use the first comma after hundreds place which is three digits from the right. The second comma comes after two digits i.e. five digits from the right. The third comma comes after another two digits which is seven digits from the right.
For Example: 5, 44, 12, 940
International System of Numeration

Example: Expand 341,697,832
Sol:
Expanded form: 3 x 100,000,000 + 4 x 10,000,000 + 1 x 1,000,000 + 6 x 100,000 + 9 x 10,000 + 7 x 1,000 + 8 x 100 + 3 x 10 + 2 x 1
Remark: If we have to express the numbers larger than a million then we use a billion in the International System of Numeration:
1 billion = 1000 million
Large Numbers in Practice
10 millimeters = 1 centimeter
1 meter = 100 centimeters = 1000 millimeters
1 kilometer = 1000 meters
1 kilogram = 1000 grams.
1 gram = 1000 milligrams.
1 litre = 1000 millilitres
1 litre = 1000 millilitres
Large Numbers in Practice
Earlier we have learned about the units of length: centimeter (cm) for small measurements like pencils, and meter (m) for larger measurements like classrooms or school buildings. Here are some conversion factors:
(a) 10 millimeters (mm) = 1 centimeter (cm)
(b) 1 meter (m) = 100 centimeters (cm) = 1000 millimeters (mm)
(c) 1 kilometer (km) = 1000 meters (m)
- To convert 1 kilometer to millimeters:
1 km = 1000 m = 1000 × 1000 mm = 10,00,000 mm
- For weight, we use kilograms (kg) for items like rice and grams (g) for smaller quantities like ginger. Additionally, 1 kilogram is equal to 1000 grams. For very small weights, like medicine tablets, we use milligrams (mg), where 1 gram equals 1000 milligrams.
- Capacity is measured in liters (l), and 1 liter is equivalent to 1000 milliliters (ml).
Common units share prefixes such as kilo, milli, and centi. Note that kilo is the largest, milli is the smallest, and centi is 100 times smaller.
|
141 videos|210 docs|58 tests
|
FAQs on Knowing our Numbers Class 6 Notes Maths Chapter 1
| 1. What are some strategies for comparing numbers effectively? |  |
| 2. How can I determine the proper order of numbers? |  |
| 3. What does "shifting digits" mean in the context of numbers? |  |
| 4. How does the introduction of 10,000 impact number understanding? |  |
| 5. Why is it important to use commas in large numbers? |  |

















