Algebraic Expressions Class 7 Notes Maths Chapter 10

An Algebraic Expression is the combination of constant and variables. We use the operations like addition, subtraction etc to form an algebraic expression.

Variable

A variable does not have a fixed value .it can be varied. It is represented by letters like a, y, p m etc.

Constant

A constant has a fixed value. Any number without a variable is a constant.
Example
1. 2x + 7
Here we got this expression by multiplying 2 and x and then add 7 to it.
In the above expression, the variable is x and the constant is 7.
2. y²
We get it by multiplying the variable y to itself.

Terms of an Expression Terms

To form an expression we use constant and variables and separate them using the operations like addition, subtraction etc. these parts of expressions which we separate using operations are called Terms.
4x - y + 7
In the above expression, there are three terms, 4x, - y and 7.

Factors of a Term

Every term is the product of its factors. As in the above expression, the term 4x is the product of 4 and x. So 4 and x are the factors of that term. We can understand it by using a tree diagram.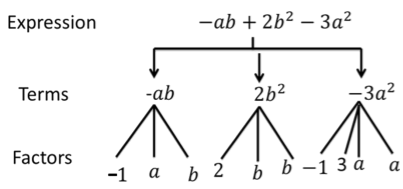

Coefficients

As you can see above that some of the factors are numerical and some are algebraic i.e. contains variable. The numerical factor of the term is called the numerical coefficient of the term.
In the above expression,
-1 is the coefficient of ab
2 is the coefficient of b²
-3 is the coefficient of a².

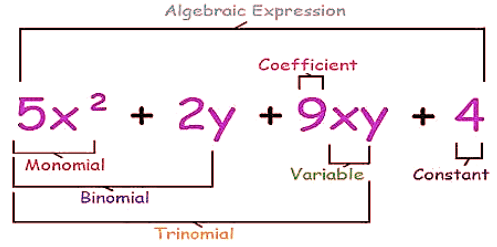
Parts of an Expression

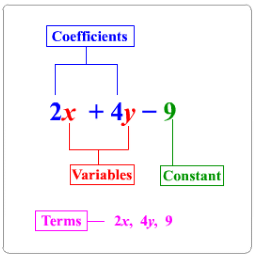Here in the above figure, you can identify the terms, variables, constants and coefficients.

Like and Unlike Terms

Like Terms are the terms which have same algebraic factors. They must have the same variable with the same exponent.
Unlike Terms are the terms which have different algebraic factors.

2x² + 3x – 5 does not contain any term with same variable.
2a² + 3a² + 7a – 7 contains two terms with same variable i.e. 2a2 and 3a2.so these are like terms.

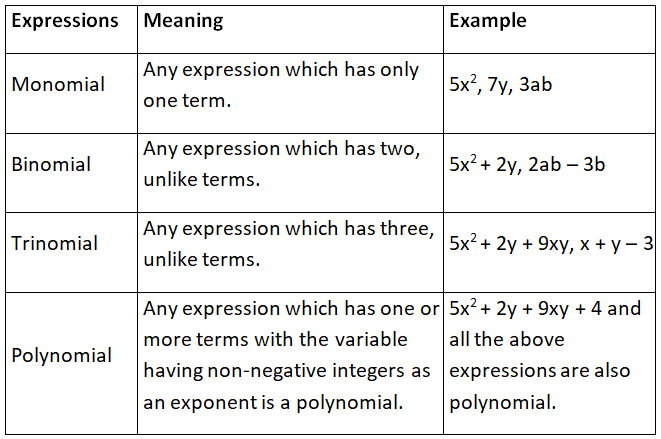
Monomials, Binomials, Trinomials and Polynomials

Addition and Subtraction of Algebraic Expression

1. Addition of Like Terms

If we have to add like terms then we can simply add their numerical coefficients and the result will also be a like term.
Example: Add 2x and 5x.
Sol: 2x + 5x
= (2 × x) + (5 × x)
= (2 + 5) × x (using distributive law)
=7 × x = 7x

2. Subtraction of Like Terms

If we have to subtract like terms then we can simply subtract their numerical coefficients and the result will also be a like term.
Example: Subtract 3p from 11p.
Solution: 11p – 3p
= (11-3) p
= 8p

3. Addition of unlike terms

If we have to add the unlike terms then we just have to put an addition sign between the terms.
Example: Add 9y, 2x and 3
Sol: We will simply write it like this-
9y + 2x + 3

4. Subtraction of Unlike Terms

If we have to subtract the unlike terms then we just have to put minus sign between the terms.
Example: Subtract 9y from 21.
Sol: We will simply write it like this-
21 - 9y

5. Addition of General Algebraic Expression

To add the general algebraic expressions, we have to arrange them so that the like terms come together, then simplify the terms and the unlike terms will remain the same in the resultant expression.
Example: Simplify the expression: 12p² – 9p + 5p – 4p² – 7p + 10
Sol: First we have to rearrange the terms.
12p² – 4p² + 5p – 9p – 7p + 10
= (12 – 4) p² + (5 – 9 – 7) p + 10
= 8p² + (– 4 – 7) p + 10
= 8p² + (–11) p + 10
= 8p² – 11p + 10

6. Subtraction of General Algebraic Expression

While subtracting the algebraic expression from another algebraic expression, we have to arrange them according to the like terms then subtract them. Subtraction is same as adding the inverse of the term.
Example: Subtract 4ab– 5b² – 3a² from 5a² + 3b² – ab
Sol: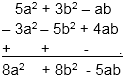 

Finding the Value of an Expression

1. Expressions with One Variable

If we know the value of the variable in the expression then we can easily find the numerical value of the given expression.
Example: Find the value of the expression 2x + 7 if x = 3.
Sol: We have to put the value of x = 3.
2x + 7
= 2(3) + 7
= 6 + 7
= 13

2. Expressions with two or more variables

To find the value of the expression with 2 variables, we must know the value of both the variables.
Example: Find the value of y² + 2yz + z² if y = 2 and z = 3.
Sol: Substitute the value y = 2 and z = 3.
y² + 2yz + z²
= 2² + 2(2) (3) + 3²
= 4 + 12 + 9
= 25

Formula and Rules using Algebraic Expression

There are so many formulas which are made using the algebraic expression.

Perimeter Formulas

• The perimeter of an equilateral triangle = 3l where l is the length of the side of the equilateral triangle by l and l is variable which can be varied according to the size of the equilateral triangle.
• The perimeter of a square = 4l where l = the length of the side of the square.
  
• The perimeter of a regular pentagon = 5l where l = the length of the side of the Pentagon and so on.

Area formulas

• The area of the square = a² where a is the side of the square
• The area of the rectangle = l × b = lb where the length of a rectangle is l and its breadth is b
• The area of the triangle = 1/2 × b × h where b is the base and h is the height of the triangle. Here if we know the value of the variables given in the formulas then we can easily calculate the value of the quantity. 

Example: What is the perimeter of a square if the side of the square is 4 cm?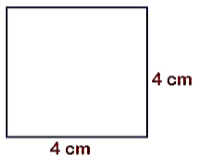
Sol: The perimeter of a square = 4l
l = 4 cm
4 × 4 = 16 cm

Rules for the Number Pattern

• If we denote a natural number by n then its successor will always be (n + 1). If n = 3 then n + 1 will be 3 + 1 = 4.
• If we denote a natural number by n then 2n will always be an even number and (2n + 1) will always be an odd number. If n = 3 then 2n = 2(3) = 6(even number), n = 3 then 2n + 1 = 2(3) + 1 = 7 (odd number)
•  If we arrange the multiples of 5 in ascending order then we can denote it by 5n. If we have to check that what will be the 11th term in this series then we can check it by 5n. n = 11 so 5n = 5(11) = 55.

Pattern in geometry

The number of diagonals which we can draw from one vertex of any polygon is (n – 3) where n is the number of sides of the polygon.
How many diagonals can be drawn from the one vertex of a hexagon?

The number of diagonals will be (n -3).
The number of sides in a hexagon is 8 so (n - 3) = (8 - 3) = 5