Exponents and Powers Class 7 Notes Maths Chapter 10
When the numbers given are very large like 54,32,00,00,000 then it is not easy to read them so we write them in the form of exponents.
Exponents make these numbers easy to read, write, understand and compare.
Exponents
To write the large numbers in short form, we use exponents.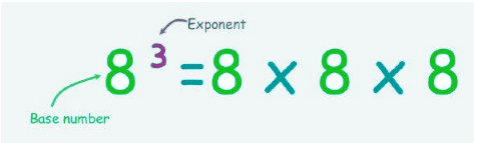 Here 8 is the base, 3 is the exponent and 83 is the exponential form of 512.
Here 8 is the base, 3 is the exponent and 83 is the exponential form of 512.
This can be read as “8 raised to the power of 3”.
The Expanded form of Natural Numbers
When we write the expanded form of a natural number then it can be written in exponential form.
Example: 247983 = 2 × 100000 + 4 × 10000 + 7 × 1000 + 9 × 100 + 8 × 10 + 3 × 1
= 2 × 105 + 4 × 104 + 7 × 103 + 9 × 102 + 8 × 101 + 3 × 1
Some Important Points to Remember
- (-1)odd number = (-1)
- (-1)even number = (1)
- a3b2 ≠ a2b3
- a2b3 = b3a2
Laws of Exponents
1. How to multiply powers with the same base?
If we have to multiply the powers which have the same base then we have to add the exponents.
am × an = am + n
Example: 83 × 84 = 83 + 4 = 87
2. How to divide powers with the same base?
If we have to divide the powers which have the same base then we have to subtract the exponents.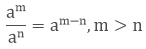
Example: 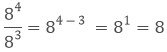
3. How to take the power of a power?
If we have to take the power of a power then we have to multiply the exponents.
(am)n = amn
Example: (83)4 = 83 × 4 = 812
4. How to multiply the powers with the same exponents?
If we have to multiply the powers where the base is different but exponents are same then we will multiply the base.
ambm = (ab)m
Example: 8343 = (8× 4)3 = 323
5. How to divide the powers with the same exponents?
If we have to divide the powers where the base is different but exponents are same then we will divide the base.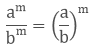
Example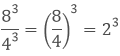
6. Numbers with Exponent Zero
Any number with zero exponents is equal to one irrespective of the base.
a°= 1
Example: 8° = 1
7. Numbers with Exponent One
Any number with one as the exponent is equal to the number itself.
a1 = a
Example: 81 = 8
8. Power with a Negative Exponent
Negative exponents can be converted into positive exponents.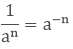
Example: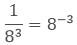
Miscellaneous Examples
Example 1: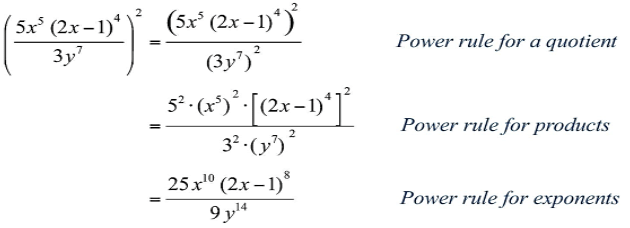
Example 2: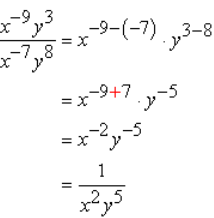
Expressing Large Numbers in the Standard Form
If we have to write very large numbers then to make them easy to read and understand we can write them in the standard form using decimals and exponents from 1.0 to 10.0.
85 = 8.5 × 10 = 8.5 × 101
850 = 8.5 × 100 = 8.5 × 102
8500 = 8.5 × 1000 = 8.5 × 103
8500 = 8.5 × 10000 = 8.5 × 104 and so on.
|
77 videos|386 docs|39 tests
|
FAQs on Exponents and Powers Class 7 Notes Maths Chapter 10
| 1. What are exponents and how are they used in mathematics? |  |
| 2. How do you write the expanded form of natural numbers using exponents? |  |
| 3. What are the laws of exponents and how do they work? |  |
| 4. How can understanding exponents and powers benefit students in their mathematical studies? |  |
| 5. Can you provide some real-life examples of how exponents are used outside of the classroom? |  |

















