Important Questions: Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce PDF Download
Q1: Find the radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm (use π = 22/7).
Ans: Given,
Length of the arc = l = 37.4 cm
Central angle = θ = 60° = 60π/180 radian = π/3 radians
We know that,
r = l/θ
= (37.4) * (π / 3)
= (37.4) / [22 / 7 * 3]
= 35.7 cm
Hence, the radius of the circle is 35.7 cm.
Q2: Find the value of √3 cosec 20° – sec 20°.
Ans: √3 cosec 20° – sec 20°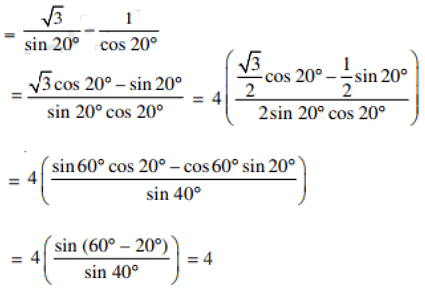
Q3: Prove that: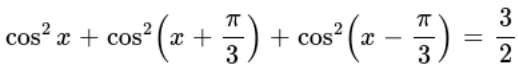
Ans: LHS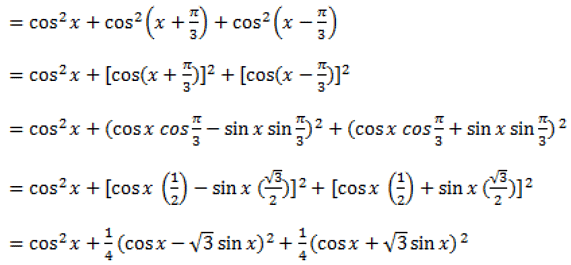
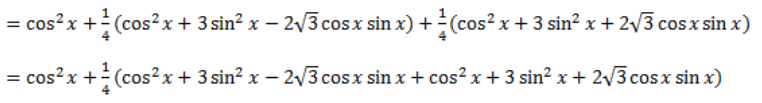
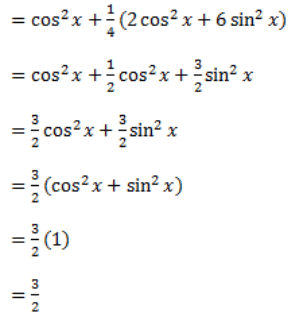
Q4: Find the general solution of the following equation.
cot2θ + 3/sin θ + 3 = 0
Ans: Given,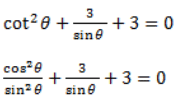
cos2θ + 3 sin θ + 3 sin2θ = 0
1 – sin2θ + 3 sin θ + 3 sin2θ = 0
2 sin2θ + 3 sin θ + 1 = 0
2sin2θ + 2 sin θ + sin θ + 1 = 0
2 sin θ (sin θ +1 ) + 1 (sin θ + 1) = 0
(2 sin θ + 1) (sin θ + 1) = 0
2 sin θ + 1 = 0, sin θ + 1 = 0
sin θ = -½, sin θ = -1
θ = nπ – (-1)n π/6, θ = nπ – (-1)n π/2; n ∈ Z
Q5: No. 10: Prove that:
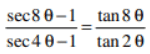
Ans:
LHS=(sec 8θ -1 )/ (sec4θ -1)
=(1/(cos8θ) -1 )/ (1/(cos4θ) -1)
=((1-cos8θ)cos4θ )/ ((1-cos4θ) cos8θ)
=(2sin2 4θcos4θ )/ ((2sin2 2θ) cos8θ)
=(2sin4θcos4θsin4θ )/ ((2sin2 2θ) cos8θ)
=(sin8θ * 2sin2θcos2θ )/ ((2sin2 2θ) cos8θ)
=(tan8θ * cos2θ )/ (sin2θ)
= (tan8θ) /(tan 2θ)
= RHS
Hence proved.
Q6: In any triangle ABC, prove that a sin (B – C) + b sin (C – A) + c sin (A – B) = 0.
Ans: In any triangle ABC,
a/sin A = b/sin B = c/sin C = k
a = k sin A, b = k sin B, c = k sin C
LHS
= a sin (B – C) + b sin (C – A) + c sin (A – B)
= k sin A [sin B cos C – cos B sin C] + k sin B [sin C cos A – cos C sin A] + k sin C [sin A cos B – cos A sin B]
= k sin A sin B cos C – k sin A cos B sin C + k sin B sin C cos A – k sin B cos C sin A + k sin C sin A cos B – k sin C cos A sin B
= 0
= RHS
Hence proved that a sin (B – C) + b sin (C – A) + c sin (A – B) = 0.
Q7: A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Ans: Given,
Number of revolutions made by the wheel in 1 minute = 360
1 minute = 60 seconds
Number of revolutions in 1 second = 360/60 = 6
Angle made in 1 revolution = 360°
Angles made in 6 revolutions = 6 × 360°
Radian measure of the angle in 6 revolutions = 6 × 360 × π/180
= 6 × 2 × π
= 12π
Hence, the wheel turns 12π radians in one second.
Q8: Show that tan 3x tan 2x tan x = tan 3x – tan 2x – tan x.
Ans: Let 3x = 2x + x
Taking “tan” on both sides,
tan 3x = tan (2x + x)
We know that,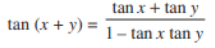
tan 3x = (tan 2x + tan x)/ (1- tan 2x tan x)
tan 3x(1 – tan 2x tan x) = tan 2x + tan x
tan 3x – tan 3x tan 2x tan x = tan 2x + tan x
tan 3x – (tan 2x + tan x) = tan 3x tan 2x tan x
Therefore, tan 3x – tan 2x – tan x = tan 3x tan 2x tan x.
Q9: Find the value of cos 570° sin 510° + sin (-330°) cos (-390°).
Ans: LHS = cos (570)sin (510) + sin (- 330)cos (- 390)
= cos (570) sin (510) + [ – sin (330) ]cos (390) [ because sin( – x ) = – sin x and cos( – x ) = cos x ]
= cos (570)sin(510) – sin (330)
= cos (90 * 6 + 30) sin (90 * 5 + 60) – sin (90 * 3 + 60) cos (90 * 4 + 30)
= – cos (30) cos (60) – [ – cos (60) ] cos (30)
= – cos (30) cos (60) + cos (30) sin (60)
= 0
Q10: Show that 2 sin2β + 4 cos (α + β) sin α sin β + cos 2 (α + β) = cos 2α.
Ans: LHS = 2 sin2β + 4 cos (α + β) sin α sin β + cos 2(α + β)
= 2 sin2β + 4 (cos α cos β – sin α sin β) sin α sin β + (cos 2α cos 2β – sin 2α sin 2β)
= 2 sin2β + 4 sin α cos α sin β cos β – 4 sin2α sin2β + cos 2α cos 2β – sin 2α sin 2β
= 2 sin2β + sin 2α sin 2β – 4 sin2α sin2β + cos 2α cos 2β – sin 2α sin 2β
= (1 – cos 2β) – (2 sin2α) (2 sin2β) + cos 2α cos 2β
= (1 – cos 2β) – (1 – cos 2α) (1 – cos 2β) + cos 2α cos 2β
= cos 2α
= RHS
Therefore, 2 sin2β + 4 cos (α + β) sin α sin β + cos 2 (α + β) = cos 2α
|
73 videos|264 docs|91 tests
|





















