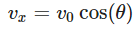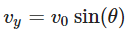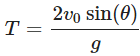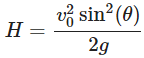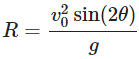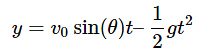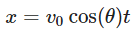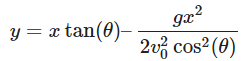Important Derivations: Motion in a Plane | Physics for JEE Main & Advanced PDF Download
Derivation 1
Time of Flight, Horizontal Range, Maximum Height and Equation of Path of Projectile in Projectile Motion
Consider a projectile launched with an initial velocity v0 at an angle θ with respect to the horizontal axis. We’ll assume no air resistance and a constant acceleration due to gravity g. The horizontal and vertical components of velocity (vx and vy) can be calculated as follows:
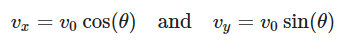
The time of flight (T) is the total time the projectile stays in the air until it returns to the same vertical position from which it was launched. The time of flight can be found using the vertical motion equation:
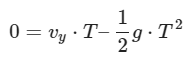
Solving for T: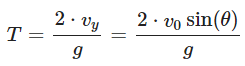
Now, the horizontal distance (R) covered by the projectile can be calculated using the time of flight: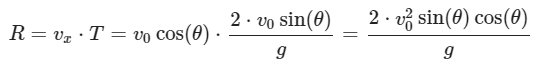
Using the identity sin(2θ)=2sin(θ)cos(θ), we can simplify: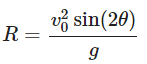
Now, let’s find the maximum height (H) reached by the projectile. The maximum height occurs when the vertical component of velocity becomes zero at the top of the trajectory. We can use the vertical motion equation: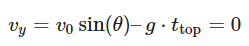
Solving for ttop: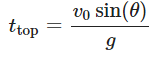
Now, we can find the maximum height (H) using the vertical motion equation: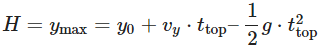

Finally, the equation of the path of the projectile (y as a function of x) is a parabolic curve: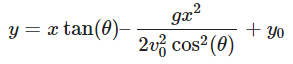
This equation represents the trajectory of the projectile launched at an angle θ from the point (x0,y0), neglecting air resistance.
Important Formulas Related to Projectile Motion
- Horizontal Velocity (vx) of the Projectile:

- Vertical Velocity (vy) of the Projectile:

- Time of Flight (T):

- Maximum Height (H):

- Range (R):

- Vertical Displacement (y) at Time t:

- Horizontal Displacement (x) at Time t:

- Equation of the Projectile’s Path:

where: v0 = Initial velocity of the projectile
θ = Launch angle
g = Acceleration due to gravity (approximately 9.81 m/s² on Earth)
|
289 videos|635 docs|179 tests
|
FAQs on Important Derivations: Motion in a Plane - Physics for JEE Main & Advanced
| 1. What are the important derivations for motion in a straight line in JEE? |  |
| 2. How do you derive the equations of motion for motion in a straight line? |  |
| 3. Can you explain the derivation of the formula for velocity in motion in a straight line? |  |
| 4. How is the formula for acceleration derived in motion in a straight line? |  |
| 5. What is the derivation of the formula for displacement in motion in a straight line? |  |

|
Explore Courses for JEE exam
|

|