Important Derivations: Current Electricity | Physics for JEE Main & Advanced PDF Download
Deduction of Ohm’s law
When a potential difference ‘V’ is applied across a conductor of length ‘l’, the drift velocity in terms of ‘V’ is given by
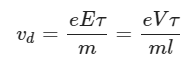 If the area of cross-section of the conductor is ‘A’ and the number of electrons per unit volume or the electron density of the conductor is ‘n’, then the current through the conductor will be
If the area of cross-section of the conductor is ‘A’ and the number of electrons per unit volume or the electron density of the conductor is ‘n’, then the current through the conductor will be
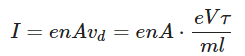
or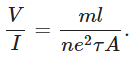
At a fixed temperature, the quantities m, l, n, e, τ and A, all have constant values for a given conductor. Therefore,

This proves Ohm’s law for a conductor and here
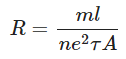
is the resistance of the conductor.
Relation between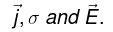
For an electron,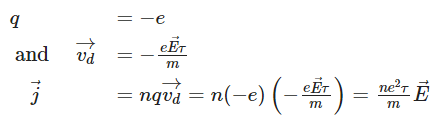
But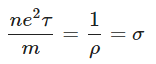 , conductivity of the conductor
, conductivity of the conductor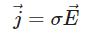 or
or
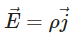
This is Ohm’s law in terms of vector quantities like current density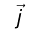 and electric field
and electric field 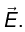
Relation between Electric Current and Drift Velocity
Number of electrons in length ‘l’ of the conductor = n * volume of the conductor =n Al
Total charge contained in length ‘l’ of the conductor is q=en Al
All the electrons which enter the conductor at the right end will pass through the conductor at the left end in time,
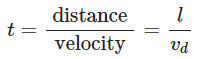
therefore, Current,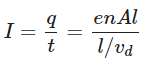
or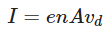
This equation relates the current ‘I’ with the drift velocity vd. The current density ‘j’ is given by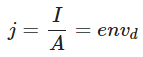 In vector form
In vector form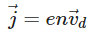 The above equation is valid for both positive and negative values of ‘q’.
The above equation is valid for both positive and negative values of ‘q’.
Expression for Internal Resistance of a Cell
To derive the expression for the internal resistance (r) of a cell in terms of electromotive force (e.m.f) (ϵ) and terminal potential difference (V) of a cell, we can use Ohm’s law and the concept of potential difference across the internal resistance.
Ohm’s Law states that the current (I) flowing through a circuit is directly proportional to the voltage (V) applied across it and inversely proportional to the total resistance (R) of the circuit: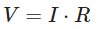
In the case of a cell, the terminal potential difference (V) is the voltage across the cell’s terminals when a current flows through it. Let’s assume that the internal resistance of the cell is r.
The e.m.f (ϵ) of the cell represents the maximum potential difference that the cell can provide when no current is flowing through it. In other words, when there is no current (I=0), the voltage across the cell terminals is equal to the e.m.f (ϵ).
Now, when a current (I) flows through the cell, there will be a voltage drop across the internal resistance (r), which we can represent as I⋅r. The remaining voltage (V–I⋅r) will be the terminal potential difference (V).
Therefore, we can write the equation for terminal potential difference as: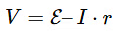
Now, we can rearrange this equation to solve for the internal resistance (r): This expression gives the internal resistance (r) of a cell in terms of the e.m.f (ϵ), terminal potential difference (V), and current (I) flowing through the cell.
This expression gives the internal resistance (r) of a cell in terms of the e.m.f (ϵ), terminal potential difference (V), and current (I) flowing through the cell.
Expression for Resistance and Resistivity
To derive the expression for the resistivity (ρ) of a conductor in terms of the number density of free electrons (n) and the relaxation time (τ), we consider the concept of electron drift in a conductor.
When an electric field (E) is applied across a conductor, the free electrons within the conductor experience a force in the direction opposite to the electric field. Due to this force, the electrons undergo random motion and also drift in the direction opposite to the electric field. The average velocity acquired by the electrons due to this drift is called the drift velocity (vd).
The drift velocity (vd) of the free electrons is related to the electric field (E) and the relaxation time (τ) through the following equation:
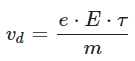 where: e = Charge of a single electron,
where: e = Charge of a single electron,
m = Mass of a single electron,
τ = Relaxation time of electrons,
E = Magnitude of the applied electric field.
The drift velocity (vd) can also be expressed in terms of the number density of free electrons (n) and the cross-sectional area of the conductor (A). The number density of free electrons (n) is the number of free electrons per unit volume. Hence, the total number of free electrons in the conductor is n⋅A⋅L, where L is the length of the conductor along the direction of the electric field.
The total charge flowing through the conductor per unit time (I, current) is given by: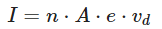
Substitute the expression for vd in terms of E and τ: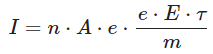 Now, the electric current (I) flowing through the conductor is related to the electric field (E) by Ohm’s law:
Now, the electric current (I) flowing through the conductor is related to the electric field (E) by Ohm’s law: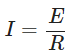 where R is the resistance of the conductor. Substitute the expression for I in terms of E and R:
where R is the resistance of the conductor. Substitute the expression for I in terms of E and R: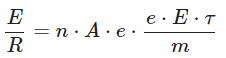 Simplify and isolate R:
Simplify and isolate R: 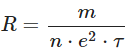 Finally, the resistivity (ρ) of the conductor is defined as the reciprocal of conductivity (σ), which is the inverse of resistivity:
Finally, the resistivity (ρ) of the conductor is defined as the reciprocal of conductivity (σ), which is the inverse of resistivity: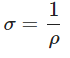 Thus, the expression for the resistivity (ρ) in terms of the number density of free electrons (n) and the relaxation time (τ) is:
Thus, the expression for the resistivity (ρ) in terms of the number density of free electrons (n) and the relaxation time (τ) is: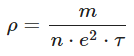
Drift Velocity Derivation
Drift velocity is defined as the average velocity attained by the particles (electrons) of a given material due to an electric field that is proportional to current. Ohm’s law can be expressed in terms of drift velocity as follows:
u=μE
Where,
u: drift velocity (m/s)
μ: material’s electron mobility (m2/V.s)
E: electric field (V/m)
Derivation of Drift velocity
Following is the derivation of drift velocity: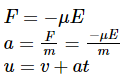
v = 0
t = T (relaxation time that is the time required by an electron to return to its initial equilibrium value)
u = aT
(substituting for v and u)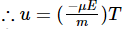
(substituting for a)
This is the final equation explaining drift velocity.
But as the temperature increases, the drift velocity of electrons increases in a metallic conductor.
|
268 videos|740 docs|171 tests
|
















