Class 9 Maths - Number System Previous Year Questions
Very Short Answer Type Questions
Q1.Complete the following: [2025]
(i) Every point on the number line corresponds to a _______ number which may be either _______ or _______.
(ii) The decimal form of an irrational number is neither _______nor _______ .
(iii) The decimal representation of the rational number8/27 is _______ .
(iv) 0 is _______number. [Hint: a rational / an irrational]
Sol:
 View Answer
View Answer 
(i) Every point on the number line corresponds to a real number which may be either rational or irrational.
(ii) The decimal form of an irrational number is neither recurring nor terminating.
(iii) The decimal representation of the rational number is 0.296.
(iv) 0 is a rational number.
Q2: Find the value of’(0.6)0 − (0.1)−1(3/8)−1 × (3/2)3 + (-1/3)−1 [2025]
 View Answer
View Answer 
Sol:
(0.6)0 − (0.1)−1(3/8)−1 × (3/2)3 + (-1/3)−1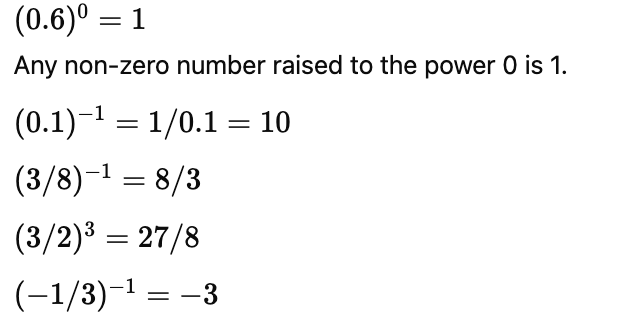

= 1-90-3
= -92
Q3: Find the value of 4(216)-2/3− 1(256)-3/4 [2023]
 View Answer
View Answer 
Sol:
4(216)-2/3− 1(256)-3/4
= 4 × (216)2/3 − (256)3/4
= 4 × (6 × 6 × 6)2/3 − (4 × 4 × 4 × 4)3/4
= 4 × 63 × 2/3 − 44 × 3/4
= 4 × 62 − 43
= 4 × 36 − 64
= 144 − 64 = 80
Short Answer Type Questions
Q1: Give three rational numbers lying between and . [2025]
 View Answer
View Answer 
Sol:The rational number lying between 1/3 and 1/2 is calculated as follows:
1/2 × ( 1/3 + 1/2 ) = 1 × (2 + 3)/ 2 × 3 × 2 = 5/12.
Therefore, 1/3 < 5/12 < 1/2.
Now, the rational number lying between 1/3 and 5/12 is calculated as:
1/2 × ( 1/3 + 5/12 ) = 1 × (4 + 5)/ 12 × 2 = 3/8.
Therefore, 1/3 < 3/8 < 5/12.
The rational number lying between 5/12 and 1/2 is:
1/2 × ( 5/12 + 1/2 ) = 1 × (5 + 6)/12 × 2 = 11/24.
Therefore, 5/12 < 11/24 < 1/2.
Hence, the three rational numbers lying between 13 and 12 are: 3/8, 5/12, and 11/24.
Q2.Identify a rational number among the following numbers : [2024]
14 + √3, 2√2, 1 and π/4
 View Answer
View Answer 
Sol: 1 is a rational number.
Q3.Simplify: (√5 + √3)2. [2023]
 View Answer
View Answer 
Sol:
Here,using (a+b)2 = a2 + 2ab +b2
we get,
(√5 + √3)2= (√5)2+ 2(√5)(√3) + (√3)2
= 5 + 2√15 + 3
= 8 + 2√15
Q4.Simplify : √45 – 3√20 + 4√5 [2022]
 View Answer
View Answer 
Sol: Simplify each square root.
√45 = √9 × 5 = 3√5
√20 = √4 × 5 = 2√5
Substitute these value in given equation : √45 – 3√20 + 4√5
we get ,
= 3√5 – 6√5 + 4√5
= √5.
Q5.Express 1.8181… in the form pq where p and q are integers and q ≠ 0. [2020]
 View Answer
View Answer 
Sol:Let x =1.8181… …(i)
[multiplying eqn. (i) by 100]
we get ,
100x = 181.8181… …(ii)
99x = 180
[subtracting (i) from (ii)]
we get,
x = 180/99
Hence, 1.8181… = 180/99 = 20/11
Long Answer Type Questions
Q1.Simplify the expression: (11 + √11) (11 – √11) [2025]
 View Answer
View Answer 
Sol:Using Identity: (a – b) (a+b) = a2 – b2
(i) (11 + √11) (11 – √11)
= 112 – (√11)2
= 121 – 11
= 110
Q2.Rationalise the denominator : [2022]
(3√2 + 1) / (2√5 − 3)
 View Answer
View Answer 
Sol: Multiply and divide the given number by 2√5 + 3
(3√2 + 1) / (2√5 − 3)
= (3√2 + 1) × (2√5 + 3) / (2√5 − 3)(2√5 + 3)
= (6√10 + 9√2 + 2√5 + 3) / (20 − 9)
= (6√10 + 9√2 + 2√5 + 3) / 11
Q3. Simplify and find the value of [2021]
(a) (729)1/6
(b) (64)2/3
(c) (243)6/5
(d) (21)3/2 x (21)5/2
(e) (81)1/3(81)1/12
 View Answer
View Answer 
Sol:
(a) (729)1/6
Prime factorize 729 = 3 × 3 × 3 × 3 × 3 × 3 = 36
(729)1/6 = (36)1/6 = (3)(6/6) = 3
( Used : Rule of exponents used: (ax)y = axy)(b) (64)2/3
Prime factorize 64 = 2 × 2 × 2 × 2 × 2 × 2 = 26
(64)2/3 = (26)2/3 = (2)(12/3) = (2)4 = 16
Rule of exponents used: (ax)y = axy)
(c) (243)6/5
(243)6/5 = (35)6/5 = 36 = 729
( Used : Rule of exponents used: (ax)y = axy)
(d) (21)3/2 x (21)5/2
(21)3/2 x (21)5/2 = (21) 3/2+5/2 = (21)8/2 = 214 = 194481
Rule of exponents used: (ax) × (ay) = ax + y
(e) (81)1/3(81)1/12
= (81)1/3(81)1/12 = (81)1/3 − 1/12
= (81)(4 − 1)/12 = (81)3/12
= (81)1/4
Prime factorize 81 = 3 × 3 × 3 × 3 = 34
(81)1/4 = (34)1/4 = (3)4/4 = 3
Rule of exponents used: axay = ax − y
Q4. Rationalize the denominator: [2020]
18 + 3√5
 View Answer
View Answer 
Sol: Multiply and divide by the (8 - 3√5):
= 18 + 3√5 × 8 − 3√58 − 3√5
= 8 − 3√582 − (3√5)2
= 8 − 3√564 − 45
= 8 − 3√519
Q5 : What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer. [2019]
 View Answer
View Answer 
Sol: 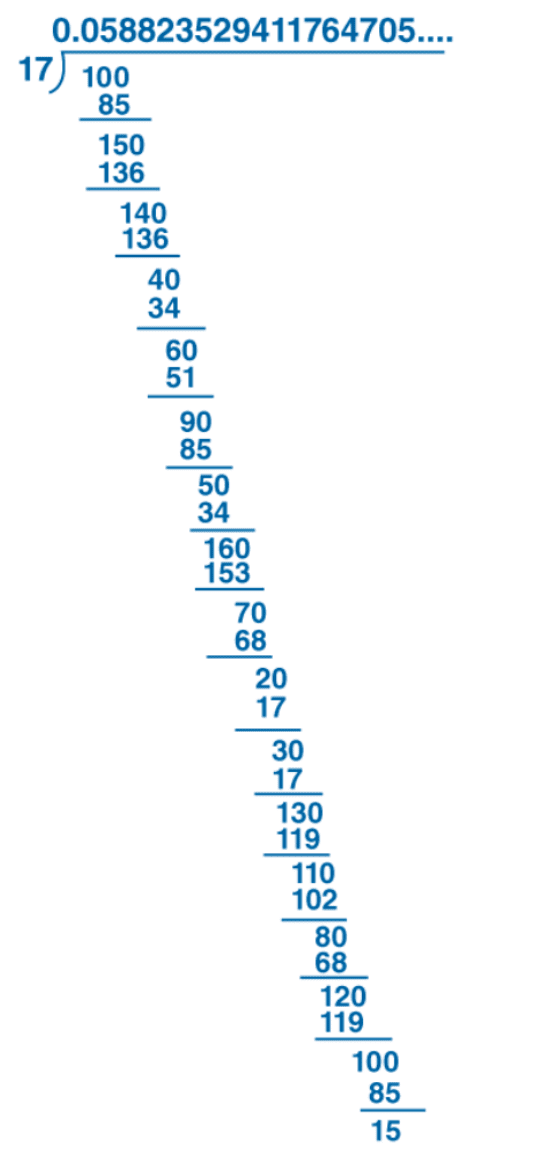
Thus, 1/17 = 0.0588235294117647….
Therefore, 1/17 has 16 digits in the repeating block of digits in the decimal expansion.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths - Number System Previous Year Questions
| 1. What is the importance of number systems in mathematics? |  |
| 2. What are the different types of number systems commonly used? |  |
| 3. How do you convert a decimal number to a binary number? |  |
| 4. What are some common operations performed on number systems? |  |
| 5. Why is it essential to understand number systems for competitive exams? |  |






















