Final Revision: Quantitative Aptitude For CAT | IPMAT Mock Test Series - Commerce PDF Download
Important Formulas for Time and Work
Knowing the formulas can completely link you to a solution as soon as you read the question. Thus, knowing the formula for any numerical ability topic make the solution and the related calculations simpler.
Given below are a few such important time and work formulas for your reference:
- Work Done = Time Taken × Rate of Work
- Rate of Work = 1 / Time Taken
- Time Taken = 1 / Rate of Work
- If a piece of work is done in x number of days, then the work done in one day = 1/x
- Total Wok Done = Number of Days × Efficiency
- Efficiency and Time are inversely proportional to each other
- X:y is the ratio of the number of men which are required to complete a piece of work, then the ratio of the time taken by them to complete the work will be y:x
- If x number of people can do W1 work, in D1 days, working T1 hours each day and the number of people can do W2 work, in D2 days, working T2 hours each day, then the relation between them will be
Important Formulas for
Ratio & Proportion
- If a : b : : c : d, then ad = bc
- If a : b : : c : d, then a + b : b : : c + d : d
- If a : b : : c : d, then a - b : b : : c - d : d
- If a : b : : c : d, then a + b : a - b : : c + d : c - d
- if
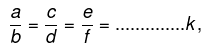 then
then 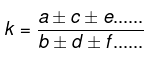
Important Formulas for
Averages
Averages can be defined as the central value in a set of data.
- Average can be calculated simply by dividing the sum of all values in a set by the total number of values.
- In other words, an average value represents the middle value of a data set. The data set can be of anything like age, money, runs, etc.

Some Basic Formulae to Remember
- Simple Average =
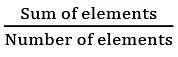
- Weighted Average =
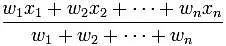
- Arithmetic Mean = (a1 + a2 + a3 ….an) / n
- Geometric Mean =

- Harmonic Mean =
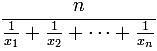
- For two numbers a and b:
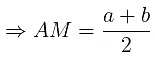
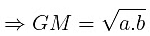
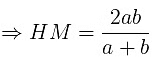
Important Formulas for Percentage
- Percent implies “for every hundred”.
% is read as percentage and x % is read as x per cent. - To calculate p % of y
(p/100) x y = (p x y)/100
p % of y = y % of p - To find what percentage of x is y: y/x × 100
- To calculate percentage change in value
Percentage change = {change/(initial value)} x 100 - Percentage point change = Difference of two percentage figures
- Increase N by S % = N( 1+ S/100 )
- Decrease N by S % = N (1 – S/100)
- If the value of an item goes up/down by x%, the percentage reduction/increment to be now made to bring it back to the original point is 100x/ (100 + x) %.
- If A is x% more /less than B, then B is 100x/(100 + x) % less/more than A.
- If the price of an item goes up/down by x %, then the quantity consumed should be reduced by 100x/ (100 + x)% so that the total expenditure remains the same.
- Successive Percentage Change
If there are successive percentage increases of a % and b%, the effective percentage increase is:
{(a + b + (ab/100)}% - Percentage – Ratio Equivalence:
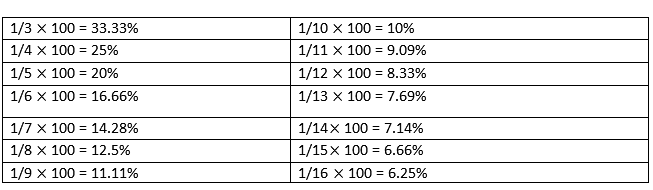 N is Numerator
N is Numerator
D is the Denominator - Product Stability Ratio:
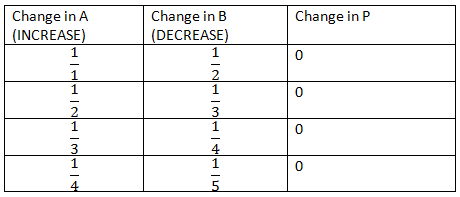
A × B = P
If A is increased by a certain percentage, then B is required to be decreased by a certain percentage to keep the product P stable.Expressing the percentage figures in ratios:
- If the price of a commodity increase by P%, then the reduction in consumption so as not to increase the expenditure is:
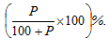
- If the price of a commodity decrease by P%, the the increase in consumption so as not to decrease the expenditure is:
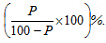
Important Formulas for Time, Speed, and Distance
- Speed = distance ÷ time
- Distance = speed × time
- Time = distance ÷ speed
- Work = time × distance
Units
- Time: seconds(s), minutes (min), hours (hr)
- Distance: (meters (m), kilometers (km), miles, feet
- Speed: m/s, km/hr
Conversions
- 1 km/h = 5/18 m/s
- 1 m/s = 18/5 km/h
- 1 km/h = 5/8 mile/s
- 1 mile/h = 22/15 foot/s
Important Formulas for Geometry
1. Quadrants
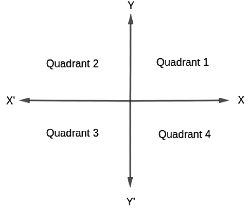
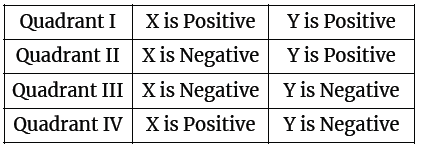
2. Lines and Angles
(a) Collinear points:
Three or more points lying on the single straight line.
In this diagram the three points A,B and C are collinear
(b) Concurrent lines:
If three or more lines lying in the same plane intersect at a single point then those lines are called concurrent lines.
The three lines X, Y and Z are concurrent lines here.
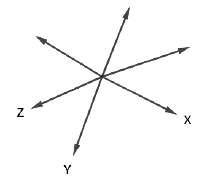
- The distance between two points with coordinates
(X1,Y1), (X2,Y2) is given by D =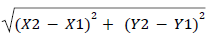
- Slope,
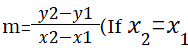 then the lines are perpendicular to each other)
then the lines are perpendicular to each other) - Mid point between two points A(x1, y1 ) and B (x2, y3) is
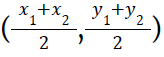
- When two lines are parallel, their slopes are equal i.e m1 = m2
- When two lines are perpendicular, product of their slopes = -1 i.e m1 * m2 = -1
- If two intersecting lines have slopes m1 and m2 then the angle between two lines will be
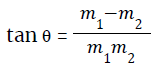 (where θ is the angle between the lines)
(where θ is the angle between the lines) - The length of perpendicular from a point (X1,Y1) on the line AX+BY+C = 0 is
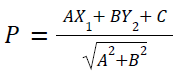
- The distance between two parallel lines
 is
is
- Coordinates of a point P that divides the line joining A (x1,y1) and B (x2,y2) internally in the ratio l:m :
- Coordinates of a point P that divides the line joining
A (x1,y1) and B (x2,y2) externally in the ratio l:m :
- For a triangle ABC, A (x1,y1), B (x2,y2), C (x3,y3):
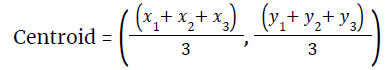
- Incentre
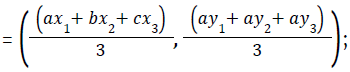
where a, b and c are the lengths of the BC, AC and AB respectively.
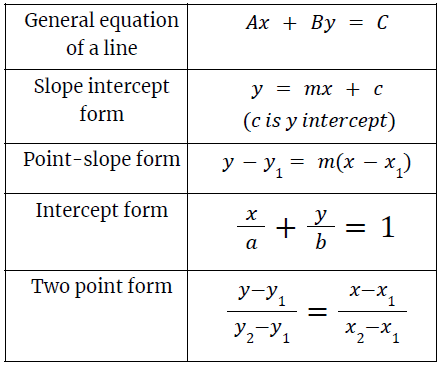
3. Equations of a lines
4. General equation of a circle
- The general equation of a circle is
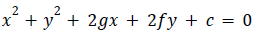
- Centre of the circle is (-g,-f)
- Radius of the circle
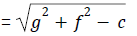
- If the origin is the center of the circle then equation of the circle is x2 + y2 = r2
- When two angles A and B are complementary, sum of A and B is 90°
- When two angles A and B are supplementary, sum of A and B is 180°
- When two lines intersect, opposite angles are equal. Adjacent angles are supplementary
- When any number of lines intersect at a point, the sum of all the angles formed = 360°
- Consider parallel lines AB, CD and EF as shown in the figure.
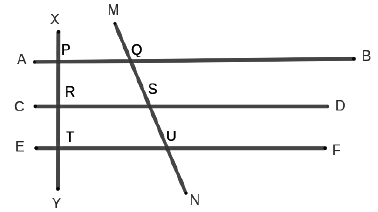
- XY and MN are known as transversals
- ∠XPQ = ∠PRS = ∠RTU as corresponding angles are equal
- Interior angles on the side of the transversal are supplementary. i.e. ∠PQS + ∠QSR = 180°
- Exterior angles on the same side of the transversal are supplementary. i.e. ∠MQB + ∠DSU = 180°
- Two transversals are cut by three parallel lines in the same ratio i.e.
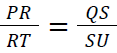
5. Triangles
- Sum of all angles in a triangle is 180°
- An angle less than 90° is called an acute angle.
- An angle greater than 90° is called an obtuse angle.
- A triangle with all sides unequal is called scalene triangle
- A triangle with two sides equal is called an isosceles triangle. The two angles of an isosceles triangle that are not contained between the equal sides are equal.
- A triangle with all sides equal is called an equilateral triangle. All angles of an equilateral triangle equal 60°.
- If in a triangle all of its angles are less than 90° than that triangle is called as acute angled triangle
- A triangle with one of its angle equal to 90° than that triangle is called as Right angled triangle
- A triangle with one of its angles greater than 90° than that triangle is called an Obtuse angled triangle.
- If one side of a triangle is produced then that exterior angle formed is equal to the sum of opposite
- remote interior angles
- A line joining the mid point of a side with the opposite vertex is called a median. (Here D is the midpoint of the AC side or AD = DC). BD is the median of this triangle ABC.
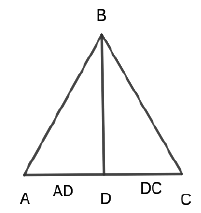
A perpendicular drawn from a vertex to the opposite side is called the altitude
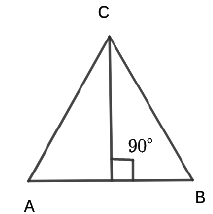
- A line that bisects and also makes right angle with the same side of the triangle is called perpendicular bisector
- A line that divides the angle at one of the vertices into two parts is called angular bisector
- All points on an angular bisector are equidistant from both arms of the angle.
- All points on a perpendicular bisector of a line are equidistant from both ends of the line.
- In an equilateral triangle, the perpendicular bisector, median, angle bisector and altitude (drawn
- from a vertex to a side) coincide.
- The point of intersection of the three altitudes is the Orthocentre.
- The point of intersection of the three medians is the centroid.
- The three perpendicular bisectors of a triangle meet at a point called the Circumcentre. A circle drawn from this point with the circumradius would pass through all the vertices of the triangle.
- The three angle bisectors of a triangle meet at a point called the incentre of a triangle. The incentre is equidistant from the three sides and a circle drawn from this point with the inradius would touch all the sides of the triangle.
- Sum of any two sides of a triangle is always greater than its third side
- Difference of any two sides of a triangle is always lesser than it’s third side
(a) Pythagoras theorem
In a right angled triangle ABC where ∠B= 90°,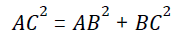
(b) Apollonius theorem
In a triangle ABC, if AD is the median to side BC then by Apollonius theorem,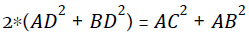
(c) Mid Point Theorem
The line joining the midpoint of any two sides in a triangle is parallel to the third side and is half the length of the third side. If X is the midpoint of CA an Y is the midpoint of CB. Then XY will be parallel to AB and XY = ½ * AB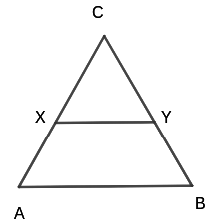 (d) Similar triangles
(d) Similar triangles
If two triangles are similar then their corresponding angles are equal and the corresponding sides will be in proportion.
For any two similar triangles:
- Ratio of sides = Ratio of medians = Ratio of heights
= Ratio of circumradii = Ratio of Angular bisectors - Ratio of areas = Ratio of the square of the sides.
Tests of similarity : (AA / SSS / SAS)
(e) Congruent triangles
If two triangles are congruent then their corresponding angles and their corresponding sides are equal. Tests of congruence : (SSS / SAS / AAS / ASA)
(f) Area of a triangle:
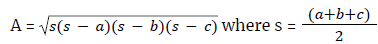
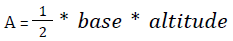
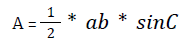 (C is the angle formed between sides a and b)
(C is the angle formed between sides a and b)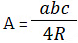 where R is the circumradius
where R is the circumradius- A = r * s where r is the inradius and s is the semi perimeter. (where a, b and c are the lengths of the sides BC, AC and AB)
(f) Special triangles :
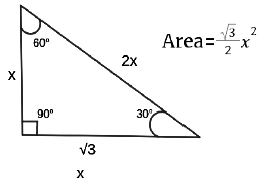
- 300, 600, 900
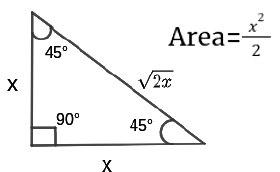
- 450, 450, 900
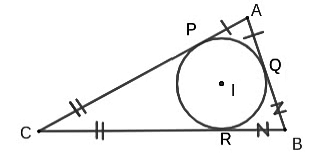
- Consider the triangle ABC with incentre I, and the incircle touching the triangle at P,Q,R as shown in the diagram. As tangents drawn from a point are equal, AP=AQ, CP=CR and BQ=BR.
- In an equilateral triangle, the centroid divides the median in the ratio 2:1. As the median is also the perpendicular bisector, angle bisector, G is also the circumcentre and incentre.
- If a is the side of an equilateral triangle, circumradius =a/√3 and inradius = a/(2√3 )
Important Formulas for Probability
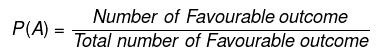
Or,
P(A) = n(A)/n(S)
Where,
- P(A) is the probability of an event “A”
- n(A) is the number of favourable outcomes
- n(S) is the total number of events in the sample space
Note: Here, the favourable outcome means the outcome of interest.
Basic Probability Formulas
Let A and B are two events. The probability formulas are listed below: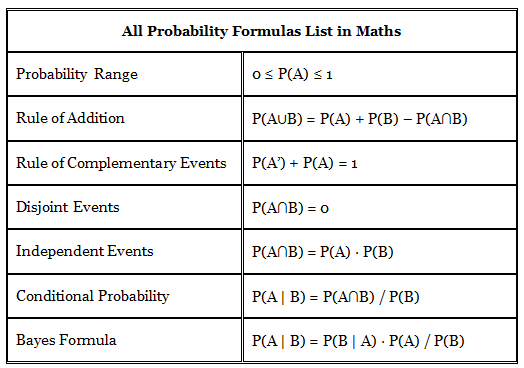
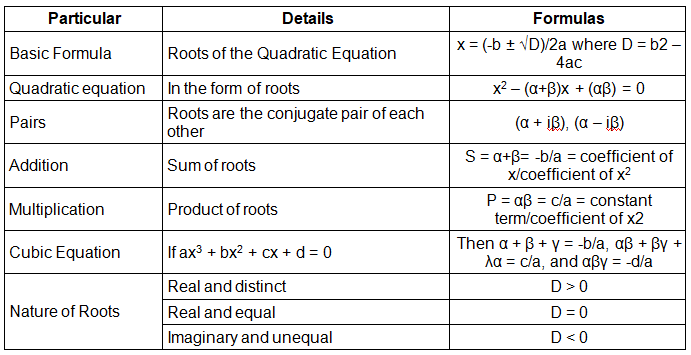
Important Formulas for Quadratic Equation
Important Formulas for Linear Equation

Important Formulas for Trigonometry
Trigonometric Identities:
- Sine = Opposite/Hypotenuse
- Secant = Hypotenuse/Adjacent
- Cosine = Adjacent/Hypotenuse
- Tangent = Opposite/Adjacent
- Co−Secant = Hypotenuse/Opposite
- Co−Tangent = Adjacent/Opposite
The reciprocal identities are given as:
- cosec θ = 1/sin θ
- sec θ = 1/ cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
Important Formulas for Logarithms
- logx 1 = 0
logx x = 1
logx (mn) = logx m + logx n
logx (m/n) = logx m – logx n
logx ab = b logx a
logx ax = a
logx m = (logy n) x (loga n)
Important Formulas for Permutation and Combination
1. Factorial Notation
Let n be a positive integer. Then, factorial n, denoted n! is defined as:
n! = n(n - 1)(n - 2) ... 3.2.1.
Examples:
- We define 0! = 1.
- 4! = (4 x 3 x 2 x 1) = 24.
- 5! = (5 x 4 x 3 x 2 x 1) = 120.
2. Permutations
The different arrangements of a given number of things by taking some or all at a time, are called permutations.
Examples:
- All permutations (or arrangements) made with the letters a, b, c by taking two at a time are (ab, ba, ac, ca, bc, cb).
- All permutations made with the letters a, b, c taking all at a time are:
(abc, acb, bac, bca, cab, cba)
3. Number of Permutations
Number of all permutations of n things, taken r at a time, is given by:
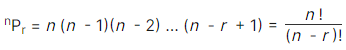
Examples
6P2 = (6 x 5) = 30.
7P3 = (7 x 6 x 5) = 210.
Cor. number of all permutations of n things, taken all at a time = n!.
4. An Important Result
If there are n subjects of which p1 are alike of one kind; p2 are alike of another kind; p3 are alike of third kind and so on and pr are alike of rth kind,
such that (p1 + p2 + ... pr) = n.
Then, number of permutations of these n objects is 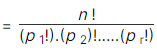
5. Combinations
Each of the different groups or selections which can be formed by taking some or all of a number of objects is called a combination.
Examples:
- Suppose we want to select two out of three boys A, B, C. Then, possible selections are AB, BC and CA.
Note: AB and BA represent the same selection. - All the combinations formed by a, b, c taking ab, bc, ca.
- The only combination that can be formed of three letters a, b, c taken all at a time is abc.
- Various groups of 2 out of four persons A, B, C, D are:
- AB, AC, AD, BC, BD, CD.
- Note that ab ba are two different permutations but they represent the same combination.
6. Number of Combinations:
The number of all combinations of n things, taken r at a time is: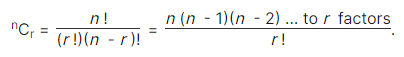
Note:
- nCn = 1 and nC0 = 1.
- nCr = nC(n - r)
Important Formulas for Interest (Simple and Compound)
- When interest is compounded Annually:
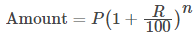
- When interest is compounded, Half-yearly:
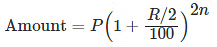
- When interest is compounded Quarterly:
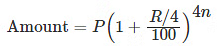
- When interest is compounded annually but time is in fraction, say 3 2/5 years:
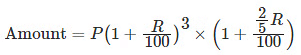
- When rates are different for different years, say R1%, R2%, R3% for 1st, 2nd and 3rd year, respectively.
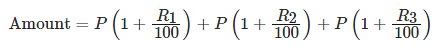
- Present worth of Rs. x due n years hence is given by:

Important Formulas for Profit, Loss and Discount
Profit = SP – CP
Profit Percentage = (SP – CP)/CP x 100
Loss = CP – SP
Loss Percentage = (CP – SP)/CP x 100
Discount = MP – SP
Discount Percentage = (MP – SP)/MP x 100
Total Discount on successive discounts of a% followed by b% = (a + b – ab/100)%
If articles worth Rs. b are free along with articles worth Rs. a, Discount = y/(x+y) x 100
Important Formulas for Square Root and Cube Root
1. Square Root:
If x2 = y, we say that the square root of y is x and we write √y = x
Thus, 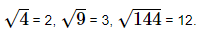
2. Cube Root:
The cube root of a given number x is the number whose cube is x.
We, denote the cube root of x by ∛x
Thus, 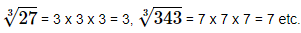
Important Formulas for Progressions (Sequences & Series)

Important Formulas for Mixtures and Alligations
If two ingredients are mixed, then
(Quantity of cheaper / Quantity of dearer) = (C.P. of dearer – Mean Price / Mean price – C.P. of cheaper)
Coordinate Geometry
The Distance Between two Points A and B:
- AB² = (Bx – Ax)² + (By – Ay)²
The Midpoint of a Line Joining Two Points
The midpoint of the line joining the points (x1, y1) and (x2, y2) is:
- [½(x1 + x2), ½(y1 + y2)]
The Equation of a Line Using One Point and the Gradient
The equation of a line that has gradient m and which passes through the point (x1, y1) is:
- y – y1 = m(x – x1)
Important Formulas for Mensuration
Rectangle
- Area = lb
- Perimeter = 2(l+b)
Square
- Area = a × a
- Perimeter = 4a
Triangle
- Area = (1/2) × b × h
or - √[s(s – a)(s – b)(s – c)], where s = (a + b + c)/2
Circle
- Area = πr² or πd²/4
- Circumference = 2πr or πd
- Area of sector of a circle = (θπr² )/360
Cube
- Volume: V = a3
- Lateral surface area = 4a²
- Surface Area: S = 6a2
- Diagonal (d) = √3 a
Cuboid
- Volume of cuboid: lbh
- Total surface area = 2 (lb + bh + hl) or 6l2
- Length of diagonal =√(l² + b² + h²)
Important Formulas for Coordinate Geometry
The Distance Between two Points A(x1, y1) and B(x2, y2):
- AB² = (x2 – x1)² + (y2 – y1)²
The Midpoint of a Line Joining Two Points
- The midpoint of the line joining the points (x1, y1) and (x2, y2) is:
[(x1 + x2)/1, (y1 + y2)/2]
The Equation of a Line Using One Point and the Gradient
- The equation of a line which has gradient m and which passes through the point (x1, y1) is:
y – y1 = m(x – x1)
Important Formulas for Inequalities
The modulus of x, |x| equals the maximum of x and –x is –|x| ≤ x ≤ |x|
1. For any two real numbers 'a' and 'b’,
- a > b => -a < -b
- |a| + |b| ≥ |a + b|
- |a| - |b| ≤ |a - b|
- |a . b| = |a| |b|
- |a| > |b| ⇒ a > b (if both are +ve)
a < b (if both are -ve)
2. For any three real numbers X, Y and Z; if X > Y then X+Z > Y+Z
- If X > Y and
(i) Z is positive, then XZ > YZ
(ii) Z is negative, then XZ < YZ
(iii) If X and Y are of the same sign, 1/X < 1/Y
(iv) If X and Y are of different signs, 1/X > 1/Y
3. For any positive real number,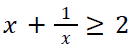
4. For any real number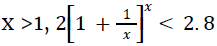
As x increases, the function tends to an irrational number called 'e' which is approx. equal to 2.718
- If |x| ≤ k then the value of x lies between –k and k, or –k ≤ x ≤ k
- If |x| ≥ k then x ≥ k or x ≤ -k
- If ax2 + bx + c < 0 then (x-m) (x-n) <0, and if n>m, then m < x < n.
- If then ax2 + bx + c > 0 then (x-m)(x-n) > 0 and if m < n, then x < m and x > n
- If ax2 + bx + c > 0 but m= n, then the value of x exists for all values, except x is equal to m, i.e., x < m and x > m but x ≠ m
Important Formulas for Set Theory
Types of Sets
1. Null Sets
- A set with zero or no elements is called a Null set.
- It is denoted by { } or Ø. Null set cardinal number is 0.
2. Singleton Sets
- Sets with only one element in them are called
- singleton sets. Ex. {2}, {a}, {0}
3. Finite and Infinite Sets
- A set having a finite number of elements is called a finite set. A set having infinite or uncountable elements in it is called an infinite set.
4. Universal Sets
- A set which contains all the elements of all the sets and all the other sets in it, is called a universal set.
5. Subsets
- A set is said to be a subset of another set if all the elements contained in it are also part of another set.
Ex. If A = {1,2}, B = {1,2,3,4} then, Set “A” is said to be a subset of set B.
6. Equal Sets
- Two sets are said to be equal sets when they contain the same elements Ex. A = {a,b,c} and B = {a,b,c} then A and B are called equal sets.
7. Disjoint Sets
- When two sets have no elements in common then the two sets are called disjoint sets. Ex. A = {1,2,3} and B = {6,8,9} then A and B are disjoint sets.
8. Power Sets
- A power set is defined as the collection of all the subsets of a set and is denoted by P(A)
- If A = {a,b} then P(A) = { { }, {a}, {b}, {a,b} }
- For a set having n elements, the number of subsets are 2n
9. Properties of Sets
- The null set is a subset of all sets
- Every set is subset of itself
- A U (BUC) = (AUB) U C
- A ∩ (B∩C) = (A∩B) ∩ C
- A U (B∩C) = (AUB) ∩ (AUC)
- A ∩ (BUC) = (A∩B) U (A∩C)
- A U Ø = A
10. Venn Diagrams
A Venn diagram is a figure to represent various sets and their relationship.
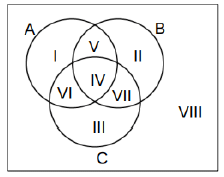
I,II,III are the elements in only A, only B & only C resp.
IV – Elements which are in all of A, B and C.
V - Elements which are in A and B but not in C.
VI – Elements which are in A and C but not in B.
VII – Elements which are in B and C but not in A.
VIII – Elements which are not in either A or B or C.
- Union of sets is defined as the collection of elements either in A or B or both. It is represented by the symbol “U”. Intersection of set is the collection of elements which are in both A and B.
- Let there are two sets A and B then,
n(AUB) = n(A) + n(B) - n(A∩B) - If there are 3 sets A, B and C then,
n(AUBUC) = n(A) + n(B) + n(C) - n(A∩B) - n(B∩C) -
n(C∩A) + n(A∩B∩C) - To maximise overlap,
- Union should be as small as possible
- Calculate the surplus = n(A) + n(B) + n(C) - n(AUBUC)
- This can be attributed to n(A∩B∩C′), n(A∩B′∩C), n(A′∩B∩C), n(A∩B∩C).
- To maximise the overlap, set the other three terms to zero.
- To minimise overlap:
- Union should be as large as possible.
Calculate the surplus = n(A) + n(B) + n(C) - n(AUBUC).
This can be attributed to n(A∩B∩C′), n(A∩B′∩C), n(A′∩B∩C), n(A∩B∩C).
To minimise the overlap, set the other three terms to maximum possible.
- Union should be as large as possible.
- Some other important properties
- A’ is called complement of set A, or A’ = U-A
- n(A-B) = n(A) - n(A∩B)
- A-B = A∩B’
- B-A = A’∩B
- (A-B) U B = A U B
|
9 videos|39 docs|10 tests
|
FAQs on Final Revision: Quantitative Aptitude For CAT - IPMAT Mock Test Series - Commerce
| 1. What are some important formulae to remember for the Quantitative Aptitude section of the CAT exam? |  |
| 2. How can I effectively revise and remember these formulae for the CAT exam? |  |
| 3. Can I rely solely on memorizing formulae for the Quantitative Aptitude section of the CAT exam? |  |
| 4. Are there any shortcuts or tricks to solve quantitative aptitude questions in the CAT exam? |  |
| 5. How important is practicing previous year question papers for the Quantitative Aptitude section of the CAT exam? |  |





















