Class 9 Maths Chapter 6 Previous Year Questions - Lines & Angles
Very Short Answer Type Questions
Q1. In a rt. ΔABC, ∠A = 90° and AB = AC. What are the values of ∠B and ∠C?
 View Answer
View Answer 
Sol. ∵ AB = AC
⇒ ∠B = ∠C
Also, ∠A = 90°
⇒ ∠B + ∠C = 90°
⇒ ∠B = ∠C = (90o/2) = 45°
Q2. In the figure, what is the value of x?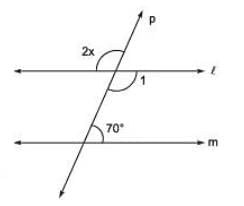
 View Answer
View Answer 
Sol. ∵ ℓ || m and p is a transversal
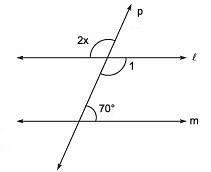
∴ ∠1 + 70° = 180° [co-interior angles]
⇒ ∠1 = 180° - 70° = 110°
Now, 2x = 110° [vertically opposite angles]
⇒ x =(110°/2) = 55°
Q3. If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3 then, what is the smaller angle?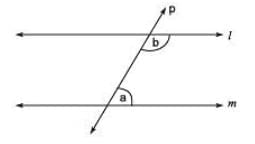
 View Answer
View Answer 
Sol. ℓ || m and p is the transversal
∴ ‘a’ and ‘b’ are interior angles on the same side of the transversal p.
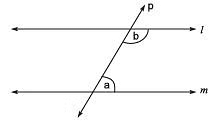
Let a = 2x and b = 3x
∴ a + b = 180°
⇒ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = (180/5)= 36°
∴ smaller angle = 2x = 2 x 36 = 72°
Q4. In the following figure AB || CD. Find the measure of ∠BOC.
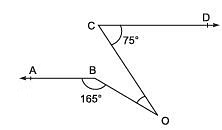
 View Answer
View Answer 
Sol. Extending AB to intersect OC, we get the following figure.
ABF is a straight line
∴ ∠OBF = 180° - 165° = 15°
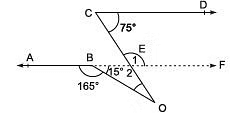
AB || CD ⇒ EF || CD
∴ ∠1 + 75° = 180°
⇒ ∠1 = 180° - 75° = 105°
⇒ ∠2 = 105°
Now, in Δ, ∠2 + 15° + ∠BOC = 180°
⇒ 105° + 15° + ∠BOC = 180°
⇒ ∠BOC = 180° - 105° - 15°
= 60°
Short Answer Type Questions
Q1. In the given figure, AB, CD, and EF are three lines concurrent at O. Find the value of y.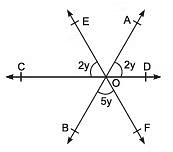
 View Answer
View Answer 
Sol:
∵ ∠AOE and ∠BOF and vertically opposite angles.
∴ ∠AOE = ∠BOF = 5y ..... (1)
Now, CD is a straight line,
⇒ ∠COE + ∠EOA + ∠AOD = 180°
⇒ 2y + 5y + 2y = 180° [From (1)]
⇒ 9y = 180°⇒ y = (180°/2)= 20°
Thus, the required value of y is 20°.
Q2. In the adjoining figure, AB || CD and PQ is a transversal. Find x.
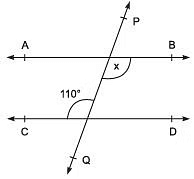
 View Answer
View Answer 
Sol:
∵ AB || CD and PQ is a transversal.
∴ ∠ BOQ = ∠ CQP [∵ Alternate angles are equal]
⇒ x = 110° [∵ ∠ CQP = 110°]
Q3. Find the measure of an angle that is 26° more than its complement.
 View Answer
View Answer 
Sol:
Let the measure of the required angle be x.
∴ Measure of the complement of x° = (90° - x)
⇒ x° - (90° - x) = 26°
⇒ x - 90° + x = 26°
⇒ 2x = 26° + 90° = 116°
⇒ x = (116°/2) = 58°
Thus, the required measure = 58°.
Q4. Two supplementary angles are in the ratio 3:2. Find the angles.
 View Answer
View Answer 
Sol:
Let the measure of the two angles be 3x and 2x.
∵ They are supplementary angles.
∴ 3x + 2x = 180°
⇒ 5x = 180° ⇒ x = (180°/5) = 36°
∴ 3x = 3 x 36° = 108° and 2x = 2 x 36° = 72°
Thus, the required angles are 108° and 72°.
Q5. In the adjoining figure, AOB is a straight line.
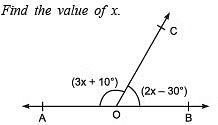
 View Answer
View Answer 
Sol:
∵ AOB is a straight line.
∴ ∠ AOC + ∠ BOC = 180°
⇒ (3x + 10°) + (2x - 30°) = 180° [Linear pair]
⇒ 3x + 2x + 10° - 30° = 180°
⇒ 5x - 20° = 180°
⇒ 5x = 180° + 20° = 200° ⇒ x = (200°/5) = 40°
Thus, the required value of x is 40°.
Q6. In the adjoining figure, find ∠ AOC and ∠ BOD.

 View Answer
View Answer 
Sol:
∵ AOB is a straight line.
∴ ∠AOC + ∠COD + ∠DOB =180°
⇒ x + 70° + (2x - 25°) = 180°
⇒ x + 2x = 180° + 25° - 70°
⇒ 3x = 205° - 70° = 135° ⇒ x = (135°/3) = 45°
∴ ∠ AOC = 45°
⇒ ∠ BOD = 2x - 25° = 2 (45°) - 25° = 90° - 25° = 65°
Q7. In the adjoining figure, AB || CD. Find the value of x.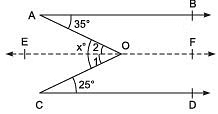
 View Answer
View Answer 
Sol:
Let us draw EF || AB and passing through point O.
∴ EF || CD and CO is a transversal.
⇒ ∠ 1 = 25° [Alternate angles]
Similarly, ∠ 2 = 35°
Adding, ∠ 1 + ∠ 2 = 25° + 35° ⇒ x = 60°
Thus, the required value of x is 60°.
Long Answer Type Questions
 View Answer
View Answer 
Q1. In the adjoining figure AB || CD || EG, find the value of x.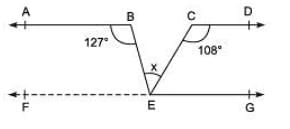 Sol:
Sol:
Through E, let us draw FEG || AB || CD.
Now, since FE || AB and BE is a transversal.
∴ ∠ ABE + ∠ BEF = 180°
[Interior opposite angles]

⇒ 127° + ∠ BEF = 180°
⇒ ∠ BEF = 180° ∠ 127° = 53°
Again, EG || CD and CE is a transversal.
∴ ∠ DCE + ∠ CEG = 180° [Interior opposite angles]
⇒ 108° + ∠ CEG = 180° ⇒ ∠ CEG = 180° - 108° = 72°
Since FEG is a straight line, then
⇒ ∠BEF + ∠BEC + ∠CEG = 180°
[Sum of angles at a point on the same side of a line = 180°]
⇒ 53° + x + 72°
= 180°
⇒ x = 180° - 53° - 72°
= 55°
Thus, the required measure of x = 55°.
|
40 videos|563 docs|57 tests
|
FAQs on Class 9 Maths Chapter 6 Previous Year Questions - Lines & Angles
| 1. What are the basic postulates of Euclid's geometry related to lines and angles? |  |
| 2. How do you define complementary and supplementary angles? |  |
| 3. What is the relationship between parallel lines and transversal angles? |  |
| 4. How can you prove that two lines are parallel using angles? |  |
| 5. What is the significance of the angle sum property of triangles? |  |

















