Important Formulas: Diagonals - GMAT PDF Download
Diagonals of Triangle
A triangle is a three-sided enclosed polygon, that has three vertices. No two vertices of the triangle are non-adjacents. Hence, a triangle does not have any diagonal.
The number of diagonals for a triangle = 0
Diagonals of Square
The diagonals of a square are the line segments that link opposite vertices of the square. A square has two diagonals. The two diagonals of the square are congruent to each other. The diagonals of a square bisect each other. Each diagonal cuts the square into two congruent isosceles right triangles.
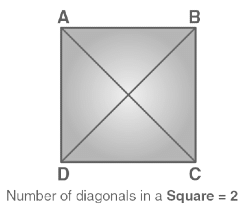
The number of diagonals of square = 2
The formula to find the length of the diagonal of a square is:
Diagonal of a Square = a√2
Where “a” is the length of any side of a square.
Diagonals of Rectangle
A rectangle has two diagonals as it has four sides. Like a square, the diagonals of a rectangle are congruent to each other and bisect each other. If a diagonal bisects a rectangle, two congruent right triangles are obtained.
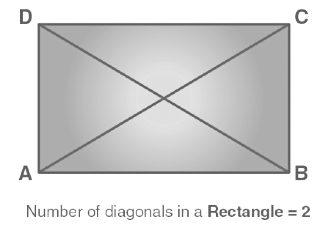
The number of diagonals of rectangle = 2
The formula to find the length of the diagonal of a rectangle is:
Diagonal of a Rectangle = √[l2 + b2]
Where “l” and “b” are the length and breadth of the rectangle, respectively.
Diagonals of Rhombus
A rhombus has four sides, and its two diagonals bisect each other at right angles. If all the angles of a rhombus are 90 degrees, a rhombus is a square. Since all the sides of the rhombus are congruent, and the opposite angles are parallel to each other, the area of the rhombus is given as:
Area of a rhombus, A = (½) pq square units
Where “p” and “q” are the two diagonals of the rhombus.
From the formula of the area of a rhombus, we can easily find the diagonal of the rhombus.
Thus, the formula to find the length of the diagonal of the rhombus is:
Diagonal of a Rhombus, p = 2(A)/q and q = 2(A)/p
Diagonals of Parallelogram
A parallelogram is a quadrilateral. The opposite sides and angles of a parallelogram are congruent, and the diagonals bisect each other. The length of the diagonals of the parallelogram is determined using the formula:
Diagonal of a parallelogram:
Diagonal, d1 = p = √[2a2+2b2 – q2]
Diagonal, d2 = q = √[2a2+2b2 – p2]
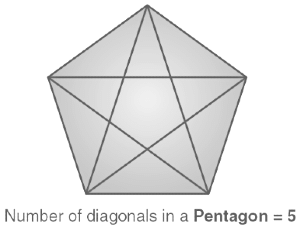
Diagonals of Pentagon
A pentagon is a five-sided closed shape or a polygon, that has five vertices. A regular polygon has all its sides equal in length. A pentagon has a total of five diagonals that are joined through opposite and non-adjacent vertices.
Diagonals of pentagon = 5
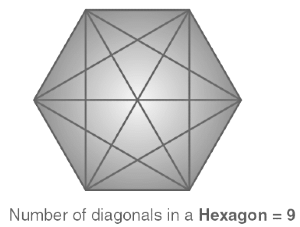
Diagonals of Hexagon
A hexagon is a six-sided closed shape that has five vertices. It is a polygon, that has a total of nine diagonals when the non-adjacent corners are joined together.
Diagonals of Hexagon = 9
Diagonals of Cube
A cube is a three-dimensional shape, that has six square faces of equal dimensions. It has 12 edges and 8 vertices. The primary diagonals of the cube are the straight lines that pass through the centre of the cube and join the opposite vertices. The diagonals of the faces of the cube are the straight lines that join the opposite vertices on each face.
Hence,
Number of primary diagonals of cube = 4
Number of diagonals on the faces of cube = 12
Total diagonals of the cube = 12 + 4 = 16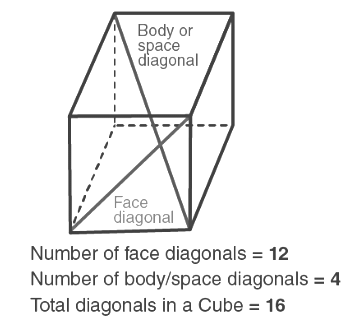
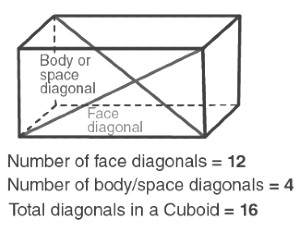
Diagonals of Cuboid
A cuboid is also a three-dimensional shape, that has six rectangular faces. Similar to the cube, it has 12 edges and 8 vertices. It is also called a rectangular prism. Since the structure of cube and cuboid are similar, therefore, the number of diagonals of both shape will also be equal.
Hence,
Number of primary diagonals of cuboid = 4
Number of diagonals on the faces of cuboid = 12
Total diagonals of the cuboid = 12 + 4 = 16
FAQs on Important Formulas: Diagonals - GMAT
| 1. What is the definition of a diagonal in a triangle? |  |
| 2. How many diagonals does a square have? |  |
| 3. Are the diagonals of a rectangle equal in length? |  |
| 4. Do the diagonals of a parallelogram bisect each other? |  |
| 5. How many diagonals does a pentagon have? |  |














