Worksheet Solutions: Units and Measurements | Physics Class 11 - NEET PDF Download
Section A. Fill in the Blanks
Q1: The standard unit of time in the International System of Units (SI) is ____________.
Ans: Second (s)
Q2: The diameter of a circle is a ___________ quantity.
Ans: Scalar
Q3: The Vernier scale is used for measuring ________.
Ans: Length
Q4: The dimensions of the coefficient of viscosity (η) are _________.
Ans: ML-1T-1
Q5: The precision of a measurement is determined by the number of ____________.
Ans: Significant Figures
Section B. Match the Column
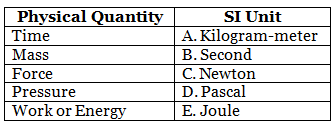
Ans: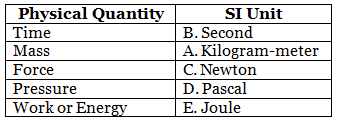
Section C. Multiple Choice Questions
Q1: Which of the following is a base unit in the International System of Units (SI)?
(a) Newton
(b) Kilogram
(c) Joule
(d) Pascal
Ans: (b) Kilogram
Q2: The least count of a Vernier caliper is 0.01 cm. If the main scale reading is 2.3 cm and the Vernier scale reading is 0.08 cm, the correct measurement is:
(a) 2.31 cm
(b) 2.32 cm
(c) 2.38 cm
(d) 2.4 cm
Ans: (a) 2.31 cm
Q3: The dimension of speed is:
(a) [M0L1T-1]
(b) [M0L0T-1]
(c) [M-1L0T-1]
(d) [M1L1T-1]
Ans: (c) [M1L0T-1]
Q4: Which of the following is not a derived unit?
(a) Newton (N)
(b) Meter (m)
(c) Watt (W)
(d) Pascal (Pa)
Ans: (b) Meter (m)
Q5: A car travels a distance of 400 meters in 20 seconds. What is its average speed?
(a) 20 m/s
(b) 40 m/s
(c) 5 m/s
(d) 2 m/s
Ans: (a) 20 m/s
Section D. Assertion Reason
Q1: Assertion: The dimensions of angular velocity are [M0L0T-1].
Reason: Angular velocity is a scalar quantity.
Ans: False
The dimensions of angular velocity are [M0L0T-2], and angular velocity is a vector quantity.
Q2: Assertion: Two physical quantities having the same dimensions are always equal. Reason: Dimensions are just labels and do not affect the numerical value of a quantity.
Ans: False
Two physical quantities having the same dimensions may not be equal; numerical values and units matter.
Section E. Case Based Questions
Case 1: A student measures the length of a pencil using two different rulers. Ruler A has a least count of 0.1 cm, and ruler B has a least count of 0.01 cm. The student obtains measurements of 7.2 cm using ruler A and 7.25 cm using ruler B. Calculate the percentage error in each measurement and discuss the precision of each ruler.
Solution: Measurement with Ruler A: Measured length = 7.2 cm Least count = 0.1 cm Percentage error = [(0.1 cm) / (7.2 cm)] × 100% = 1.39%
Measurement with Ruler B: Measured length = 7.25 cm Least count = 0.01 cm Percentage error = [(0.01 cm) / (7.25 cm)] × 100% = 0.14%
Ruler A has a higher percentage error, indicating lower precision compared to Ruler B.
Case 2: A student measures the time taken for a pendulum to complete 10 oscillations. He records three sets of measurements as follows: 14.5 s, 14.3 s, and 14.4 s. Calculate the mean time and the absolute error in the measurement.
Solution: Mean time = (14.5 s + 14.3 s + 14.4 s) / 3 = 14.4 s Absolute error = |14.4 s - 14.5 s| = 0.1 s
The mean time is 14.4 seconds, and the absolute error is 0.1 seconds.
Section F. Short Answer Type
Q1: Define dimensional analysis. How is it useful in physics? (Word Limit: 100-120 words)
Ans: Dimensional analysis is a mathematical technique used in physics to analyze and understand the relationships between physical quantities. It involves examining the dimensions (fundamental units like mass, length, time, etc.) of various physical quantities and how they combine in equations. Dimensional analysis is useful in physics for the following reasons:
- Verifying equations and identifying errors.
- Deriving new equations or relations between physical quantities.
- Checking the consistency of equations.
- Converting units from one system to another.
- Solving complex problems by identifying relevant parameters.
Q2: Explain the difference between precision and accuracy in measurements. (Word Limit: 100-120 words)
Ans: Precision and accuracy are two important aspects of measurements that describe different characteristics:
- Precision refers to the degree of consistency and repeatability in a set of measurements. A precise measurement has very little scatter or variation among repeated measurements.
- Accuracy, on the other hand, measures how close a measurement is to the true or accepted value. An accurate measurement is close to the actual or expected value, regardless of whether it is precise. In summary, precision focuses on the consistency of measurements, while accuracy deals with how close measurements are to the true value.
Q3: Differentiate between scalar and vector quantities with examples. (Word Limit: 100-120 words)
Ans: Scalar and vector quantities are types of physical quantities with distinct characteristics:
- Scalar quantities only have magnitude and no direction. Examples include mass, temperature, and time. Scalar quantities are represented by real numbers and are added algebraically.
- Vector quantities have both magnitude and direction. Examples include displacement, velocity, and force. Vector quantities are represented by arrows, where the length represents magnitude, and the direction indicates the direction. Vector quantities are added using vector addition rules. In summary, scalar quantities have magnitude only, while vector quantities have magnitude and direction.
Q4: State and explain the principle of the Vernier caliper. (Word Limit: 100-120 words)
Ans: The Vernier caliper is a precision instrument used for measuring the length of an object with high accuracy. Its principle is based on the Vernier scale, which consists of a main scale (fixed) and a Vernier scale (sliding).
The principle of the Vernier caliper is as follows:
- The main scale is divided into centimeters and millimeters, with each millimeter marked.
- The Vernier scale is a movable scale with a slightly different spacing than the main scale. It has divisions that are slightly shorter than the main scale divisions.
- When the jaws of the Vernier caliper are closed around an object, the Vernier scale is moved until the two scales align.
- The reading on the Vernier scale, along with the main scale reading, gives a highly accurate measurement, including decimal places.
Q5: Explain the concept of relative error in measurements. (Word Limit: 100-120 words)
Ans: Relative error is a measure of the accuracy of a measurement and is expressed as the ratio of the absolute error to the true value of the quantity being measured. It is often represented as a percentage. The formula for relative error is: Relative Error (%) = [(Absolute Error) / (True Value)] × 100%
Key points about relative error:
- It quantifies how far off a measurement is from the true value.
- A smaller relative error indicates a more accurate measurement.
- Relative error is dimensionless and is often expressed as a percentage.
- It is a useful metric for comparing the accuracy of different measurements or instruments.
- In general, accurate measurements have lower relative errors, while less accurate measurements have higher relative errors.
Section G. Long Answer Type
Q1: Discuss the importance of units and measurements in scientific research. (Word Limit: 150-200 words)
Ans: Units and measurements play a crucial role in scientific research for several reasons:
- Standardization: Units provide a common language for scientists worldwide. The International System of Units (SI) ensures consistency and enables scientists to communicate effectively.
- Precision: Measurements allow scientists to quantify and compare physical quantities precisely. Precise measurements help in drawing accurate conclusions and making reliable predictions.
- Verification and Validation: Measurements are essential for testing scientific theories and hypotheses. Experiments involve making measurements to validate or invalidate scientific ideas.
- Quantification: Science aims to explain natural phenomena by quantifying relationships between variables. Measurements provide the data needed to analyze and model these relationships.
- Reproducibility: Accurate measurements allow other researchers to reproduce experiments and verify scientific findings independently.
- Calibration: Measurements can be used to calibrate instruments and ensure their accuracy. Calibration is critical in various fields, including metrology and engineering. In summary, units and measurements are the foundation of scientific research, enabling scientists to quantify, analyze, and understand the natural world accurately.
Q2: Explain the principle of the Vernier scale in detail and provide a step-by-step procedure for using a Vernier caliper to measure the length of an object. (Word Limit: 150-200 words)
Ans: The Vernier caliper is a precision instrument used to measure the length, diameter, or thickness of objects with great accuracy. Its principle is based on the Vernier scale, which allows for precise readings.
Principle of the Vernier Scale:
- The Vernier scale consists of a main scale (fixed) and a Vernier scale (sliding).
- The main scale is divided into centimeters and millimeters, with each millimeter marked.
- The Vernier scale has divisions that are slightly shorter than those on the main scale.
- When the jaws of the Vernier caliper are closed around an object, the Vernier scale is moved until the two scales align.
- The reading on the Vernier scale, along with the main scale reading, provides an accurate measurement.
Procedure for Using a Vernier Caliper:
- Ensure the Vernier caliper is clean and free of debris.
- Close the jaws gently around the object you want to measure.
- Make sure the jaws are in firm contact with the object but not too tight.
- Read the main scale value that lines up with the left end of the Vernier scale.
- Next, find the Vernier scale division that best aligns with a division on the main scale.
- Note the Vernier scale value.
- Add the main scale and Vernier scale values to obtain the final measurement.
The accuracy of a Vernier caliper is typically up to 0.02 mm or 0.001 inches, making it suitable for precise measurements.
Q3: Explain the concept of significant figures in measurements. Provide examples of how to determine the number of significant figures in various measurements. (Word Limit: 150-200 words)
Ans: Significant figures (sig figs) are digits in a measurement that convey meaningful information about the precision and accuracy of that measurement. They are important for representing the uncertainty associated with a measurement. Here's how to determine the number of significant figures in various measurements:
Non-zero digits are always significant. For example:
- In 23.45, there are four significant figures.
Any zeros between significant figures are also significant. For example:
- In 1007, there are four significant figures.
Leading zeros (zeros to the left of the first non-zero digit) are not significant. For example:
- In 0.00563, there are three significant figures.
Trailing zeros (zeros to the right of non-zero digits and after the decimal point) are significant. For example:
- In 12.500, there are five significant figures.
In whole numbers without a decimal point, trailing zeros may not be considered significant. For example:
- In 5000, there are two significant figures unless specified otherwise.
In scientific notation, all digits in the coefficient are significant. For example:
- In 6.02 x 1023, there are three significant figures in 6.02.
In calculations involving measurements, the result should be rounded to the least number of significant figures in the original data to maintain accuracy and avoid false precision.
Q4: Discuss the process of dimensional analysis with an example. (Word Limit: 150-200 words)
Ans: Dimensional analysis is a powerful technique used in physics to derive relationships between physical quantities and verify equations. It is based on the principle that physical equations must be dimensionally consistent. Here's a step-by-step process of dimensional analysis with an example:
Example: Derive an equation for the period (T) of a simple pendulum using dimensional analysis.
Step 1: List the Relevant Variables
- Identify the variables involved in the problem. In this case, we have:
- Length (L) of the pendulum.
- Acceleration due to gravity (g).
- Period (T) of the pendulum.
Step 2: Write the Basic Equation
- Start with a basic equation or guess a functional relationship between the variables. In this case, we know that the period of a pendulum may depend on the length (L) and the acceleration due to gravity (g).
T = k * Lm * gn
Step 3: Assign Dimensions
- Assign dimensions to each variable. For example:
- [T] = [Lx] * [gy]
Step 4: Equate Dimensions
- Equate the dimensions on both sides of the equation:
- [T] = [Lx] * [gy]
Step 5: Solve for Exponents
- Determine the values of x and y by comparing dimensions:
- x = 1 (from [L])
- y = -1 (from [g])
Step 6: Final Equation
- Rewrite the equation with the determined exponents:
- T = k * L * (1/g)
The final equation for the period of a simple pendulum is T = k * (L / g), where k is a dimensionless constant.
Q5: Explain the concept of the International System of Units (SI) and its importance in scientific measurements. Provide examples of SI units for various physical quantities. (Word Limit: 150-200 words)
Ans: The International System of Units (SI) is a globally accepted system of measurement used in scientific research and everyday life. It is based on seven fundamental SI base units, and all other units are derived from these base units. The importance of SI units in scientific measurements is paramount due to the following reasons:
Standardization: SI provides a standardized and consistent system of units, ensuring that measurements made by scientists worldwide are easily understood and compared.
Precision: SI units are designed to be precise and based on physical constants, making them suitable for highly accurate measurements.
Interchangeability: SI units allow easy conversion between units, facilitating communication and calculations in scientific research.
Examples of SI base units:
- Length: Meter (m)
- Mass: Kilogram (kg)
- Time: Second (s)
- Electric Current: Ampere (A)
- Temperature: Kelvin (K)
- Amount of Substance: Mole (mol)
- Luminous Intensity: Candela (cd)
Examples of SI derived units:
- Force: Newton (N) = kg·m/s2
- Energy: Joule (J) = N·m
- Pressure: Pascal (Pa) = N/m2
- Velocity: Meter per second (m/s) = m/s
- Power: Watt (W) = J/s
In summary, SI units provide a standardized, precise, and internationally recognized system of measurement essential for scientific research and technological advancements.
Section H. Numericals
Q1: Find the dimensions of (a/b) in the equation:  where P is pressure, x is distance and t is time.
where P is pressure, x is distance and t is time.
Ans: 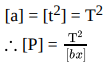
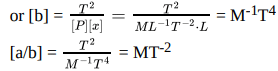
Q2: Find an expression for viscous force F acting on a tiny steel ball of radius r moving in a viscous liquid of viscosity η with a constant speed ν by the method of dimensional analysis.
Ans: It is given that viscous force F depends on (i) the radius r of steel ball, (ii) the Speed v of the tiny steel ball, and (iii) the coefficient of viscosity η of viscous liquid.
Wriring dimensional formula for given quantities, we have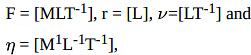
According to given condition we can write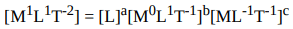
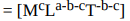
Comparing powers of M, L and T on either side of equation, we get
c = 1
a + b - c = 1
- b - c = -2
On solving, these above equations, we get
a = 1, b = 1 and c = 1
Hence, the relation becomes
f = krηv
Here, k is constant of proportionality
Q3: Suppose there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth?
Ans:
Let the period of revolution of the earth = Te
As the planet goes round the sun twice as fast as the earth, so its period of revolution is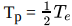
Orbital size of the earth, ac = 1 AU
Orbital size of the planet, ap = ?
From Kepler's law of periods,
Q4: A great physicist of this century (P.A.M. Dirac) loved playing with numerical values of Fundamental constants of nature. This led him to an interesting observation. Dirac found that from the basic constants of atomic physics (c, e, mass of electron, mass of proton) and the gravitational constant G, he could arrive at a number with the dimension of time. Further, it was a very large number, its magnitude being close to the present estimate on the age of the universe (15 billion years). From the table of fundamental constants in the book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants?
Ans:
Paul Dirac was a British theoretical physicist who made fundamental contributions to the development of quantum mechanics, quantum field theory and quantum electrodynamics and is particularly known for his attempts to unify the theories of quantum mechanics and relativity theory.
One relation consists of some fundamental constants that give the age of the Universe by: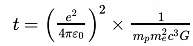
Where, t = Age of Universe, e = Charge of electrons = 1.6 x 10-19C
ε0 = Absolute permittivity, mp = Mass of protons = 1.67 x 10-27 kg
me = Mass of electrons = 9.1 x 10-31 kg c = Speed of light = 3 x 108 m/s
G = Universal gravitational constant = 6.67 x 1011 Nm2 Kg-2
Also, 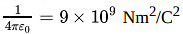
Substituting these values in the equation, we get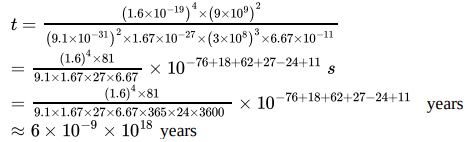
= 6 billion years (which is the approximate age of our universe)
|
95 videos|367 docs|98 tests
|
FAQs on Worksheet Solutions: Units and Measurements - Physics Class 11 - NEET
| 1. What are the basic units of measurement? |  |
| 2. How do you convert between different units of measurement? |  |
| 3. Why is it important to use standard units of measurement? |  |
| 4. What are the prefixes used in the metric system? |  |
| 5. How do you measure the volume of irregularly shaped objects? |  |





















