Class 10 Maths Chapter 9 Important Question Answers - Some Application of Trigonometry
Very Short Answer Type Questions
Q1: A ladder 15 m long leans against a wall making an angle of 60º with the wall. Find the height of the point where the ladder touches the wall.
Ans: Let the height of wall be h. As per given in question we have drawn figure below.
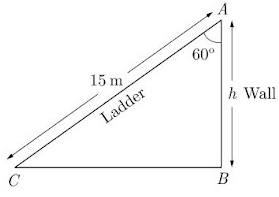
h/15 = cos60°
h = 15 x cos60°
= 15 x (1/2) = 7.5m
Q2: A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Ans: Let AC be the ladder
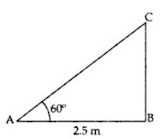
cos60° = AB/AC
1/2 = 2.5/AC
∴ Length of ladder, AC = 5 m
Q3: If the length of the ladder placed against a wall is twice the distance between the foot of the ladder and the wall. Find the angle made by the ladder with the horizontal.
Ans: Let the distance between the foot of the ladder and the wall is x, then length of the ladder will be 2x. As per given in question we have drawn figure be
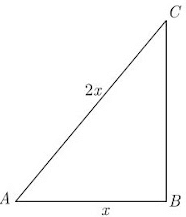
In ΔABC, ∠B = 90°
cos A = x/2x = 1/2 = cos60°
A = 60°
Q4: A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
Ans: As per given in question we have drawn figure below.
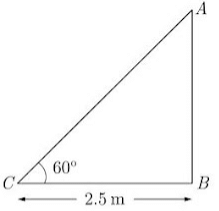
In ΔACB with ∠C = 60°, we get
Cos 60° = 2.5/AC
1/2 = 2.5/AC
AC = 2 x 2.5 = 5m
Q5: In the given figure, AB is a 6 m high pole and DC is a ladder inclined at an angle of 60° to the horizontal and reaches up to point D of pole. If AD = 2.54 m, find the length of ladder. (use √3 = 1.73)
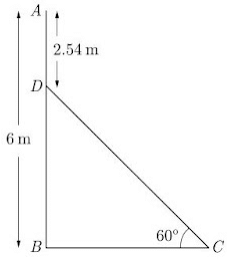
Ans: We have,
AD = 2.54 m
DB = 6 - 2.54 = 3.46 m
In △BCD,
∠B = 90°
sin 60° = BDDC
√32 = 3.46DC
DC = 3.46 × 2√3 = 3.461.73 = 4
Thus length of ladder is 4 m.
Q6: An observer 1.5 m tall is 28.5 m away from a tower 30 m high. Find the angle of elevation of the top of the tower from his eye.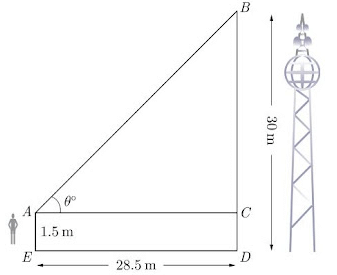
Ans: As per given in question we have drawn figure below.
Here,
AE = 1.5 m is height of observer and BD = 30 m is tower.
Now,
BC = 30 - 1.5 = 28.5 m
In △BAC,
tan θ = BCAC
tan θ = 28.528.5 = 1 = tan 45°
θ = 45°
Hence, angle of elevation is 45°.
Q7: If a tower 30 m high, casts a shadow 10√3 m long on the ground, then what is the angle of elevation of the sun?
Ans: Let required angle be θ.
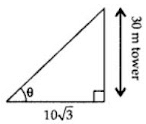
tan θ = 3010 √3
tan θ = √3
⇒ tan θ = tan 60°
∴ θ = 60°
Q8: The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x : y.
Ans: When base is same for both towers and their heights are given, i.e., x and y respectively
Let the base of towers be k.
tan 30° = xk | tan 60° = yk
x = k tan 30° = k√3 ...(i)
y = k tan 60° = k √3 ...(ii)
From equations (i) and (ii),
xy = k√3k √3 = kk × 1√3 = 13 = 1 : 3
Q9: A pole 6 m high casts a shadow 2√3 m long on the ground, then find the Sun’s elevation.
Ans: Let the Sun’s elevation be θ. As per given in question we have drawn figure below.
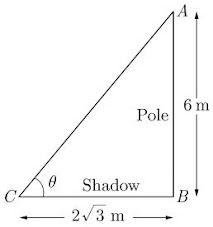
Length of pole is 6 m and length of shadow is 2√3 m.
From △ABC we have,
tan θ = ABBC = 62 √3 = 3√3 = √3 = tan 60°
θ = 60°
Hence sun’s elevation is 60°.
|
127 videos|683 docs|84 tests
|
FAQs on Class 10 Maths Chapter 9 Important Question Answers - Some Application of Trigonometry
| 1. What are some real-life applications of trigonometry? |  |
| 2. How can trigonometry be applied in construction? |  |
| 3. What is the significance of the sine and cosine functions in trigonometry? |  |
| 4. How do surveyors use trigonometry in their work? |  |
| 5. Can trigonometry be used in computer graphics? |  |






















