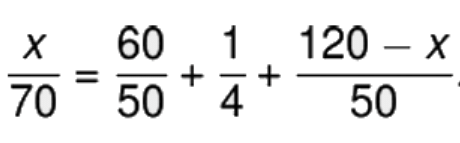Speed, Distance & Time Important Notes | Quantitative Aptitude (Quant) - CAT PDF Download
Introduction
- Speed, Distance and Time is one of the most commonly tested topics in various competitive exams. Questions from this topic have appeared consistently in various exams for the last several years.
- Competitive exams not only check for formulaic knowledge in this idea, but also for strong fundamentals and application of the concepts involved. For instance, races as an idea is built on Speed, Time and Distance as well as Ratio and Proportions.
- One can usually expect 3-4 questions from these ideas in competitive exams like CAT.
Speed, Time and Distance
Speed of a body is the distance covered by the body per unit time, i.e., Speed = Distance/Time.
- Speed: Speed is the rate at which a particular distance is covered by an object in motion.
- Time: Time is an interval separating two events.
- Distance: Distance is the extent of space between two points.
Units of Speed, Time and Distance
Each of the speed, distance and time can be represented in different units:
- Time can be generally expressed in terms of seconds(s), minutes (min) and hours (hr).
- Whereas the distance is generally expressed in meters (m), kilometres (km), centimetres (cm), miles, feet (ft), etc.
- Speed is commonly expressed in m/s, km/hr.
Example: If the distance is given in km and time in hr then as per the formula:
Speed = Distance/ Time; the unit of speed will become km/ hr.
Relationship Between Speed, Time and Distance
Now that we are well aware of the definition of speed, distance and time let us understand the relationship between them. It is said that an object attains motion or movement when it changes its position with respect to any external stationary point. Speed, Time and Distance are the three variables that represent the mathematical model of motion as, s x t = d.
- Time is directly proportional to distance. It means that speed remains constant, if we have two vehicles moving two distances for two different time duration then the time is directly proportional to the distance.
- Speed is directly proportional to distance. It means that time remains constant if we have two vehicles moving two distances at two different speeds respectively.
- Speed is inversely proportional to time. It means that distance remains constant if we have two vehicles moving at two different speeds and taking times respectively.
This shows us how slow or fast a target moves. It represents the distance covered divided by the time needed to cover the distance.
Speed is directly proportional to the given distance and inversely proportional to the proposed time. Hence,
Distance = Speed x Time and
Time = Distance / Speed since as the speed grows the time needed will decrease and vice versa.
Conversion of Speed, Time and Distance
- To convert a given data from km/hour to m/sec, we multiply by 5/18. As 1 km/hour = 5/18 m/sec.
- To convert a given data m/sec to km/hour, we multiply by 18/5. As 1 m/sec = 18/5 km/hour = 3.6 km/hour.
In terms of formula, we can list it as: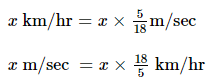
Similarly, some other conversions are given below:
- 1 km/hr = 5/8 miles/hour
- 1 yard = 3 feet
- 1 kilometer= 1000 meters
- 1 mile= 1.609 kilometer
- 1 hour= 60 minutes= 3600 seconds
- 1 mile = 1760 yards
- 1 yard = 3 feet
- 1 mile = 5280 feet
Applications of Speed, Time and Distance
Some applications of speed, time and distance are as follows:
1. Average Speed
- The average speed is determined by the formula = (Total distance travelled)/(Total time taken)
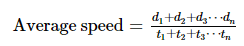
- When the distance travelled is constant and two speeds is given then the average speed can be calculated using the formula for the harmonic mean of the two speeds:
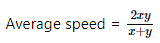
where x and y are the two speeds at which the corresponding distance has been reached. This formula works because the time taken for each leg of the journey is inversely proportional to the speed.
2. Relative Speed
The basic concept of relative speed is that the speed gets combined in the case of objects moving in the opposite direction to one another and the speed gets subtracted for the case when objects are moving in an identical direction.
(a) If two objects are moving in the opposite direction
For example, if two passenger trains are moving in the opposite direction with a speed of X km per hour and Y kilometre per hour respectively. Then their relative speed is given by the formula:- Relative speed = X + Y
- Time taken by the train in passing each other is given by the formula:
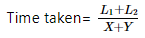
- Here L1, L2 are the lengths of the trains respectively.
(b) If two objects are moving in the same direction
On the other hand, if the two trains are travelling in the same direction with the speed of X km per hour and Y kilometers per hour respectively. Then their relative speed is given by the formula:- Relative speed = X -Y
- The time taken by the trains in crossing each other is given by the formula:
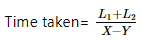
- Here L1, L2 are the lengths of the trains respectively.
Inverse Proportionality of Speed & Time:
When the distance is constant, speed and time are inversely related. When D is constant, S has an inverse relationship to 1/T. The time will be in the ratio n:m if the speeds are in the ratio m:n.
3. Motion in a Straight Line
Problems on situations of motion in a straight line are one of the most commonly asked questions in the CAT and other aptitude exams. Hence a proper understanding of the following concepts and their application to problem solving will be extremely important for the student.
Motion in a straight line is governed by the rules of relative speed .
A Two or more bodies starting from the same point and moving in the same direction: Their relative speed is S1 - S2
(a) In the case of the bodies moving to-and-fro between two points A and B:
- The faster body will reach the end first and will meet the second body on its way back.
- The relative speed S1 - S2 will apply till the point of reversal of the body and after that the two bodies will start to move in the opposite directions at a relative speed of S1+ S2 .
- The total distance covered by the two bodies = 2D
(b) In the case of the bodies continuing to move in the same direction without coming to an end point and reversing directions:
- The faster body will take a lead and will keep increasing the lead and the movement of the two bodies will be governed by the relative speed equation S1 - S2.
Moving in the opposite direction: Their relative speed will be initially given by S1+ S2.
(a) In the case of the bodies moving to-and-fro between two points A and B starting from opposite ends of the path:
- The two bodies will move towards each other, meet at a point in between A and B, then move apart away from each other. The faster body will reach its extreme point first, followed by the slower body reaching its extreme point next.
- The position of the meeting point will be determined by the ratio of the speeds of the bodies.
(b) In the case of body continuing to move in the same direction without coming to an end point and reversing directions
- The relative speed will be S1+ S2 initially while approaching each other and while moving away from each other.
Example 1: Two bodies A and B start from opposite ends P and Q of a straight road. They meet at a point 0.6D from P . Find the point of their fourth meeting?
Sol: Since time is constant, we have ratio of speeds as 3:2.
Also, total distance to be covered by the two together for the fourth meeting is 7D.
This distance is divided in a ratio of 3: 2
Thus, we have that A will cover 4.2D and B will cover 2.8D.
The fourth meeting point can then be found out by tracking either A or B's movement.
A, having moved a distance of 4.2D, will be at a point 0.2D from P.
This is the required answer.
Example 2: A starts walking from a place at a uniform speed of 2 km/h in a particular direction. After half an hour, B starts from the same place and walks in the same direction as A at a uniform speed and overtakes A after 1 hour 48 minutes. Calculate the speed of B?
Sol: From the first two sentences, you see that A is 1 km ahead of B when B starts moving.
This distance of 1 km is covered by B in 9/5 hours
The equation operational here
(SB-SA) x T = Initial Distance
(SB - 2) x 9/5 = 1
Solving, we get
SB = 23/9 km/h.
Concept of Acceleration
- Acceleration is defined as 'rate of change of speed'.
- Acceleration can be positive, zero or negative.
- When the acceleration is negative, it is called as deceleration
- The unit of acceleration is m/s2
- Formulas
(i) Acceleration = Speed / Time
(ii) Final speed = Initial speed + Acceleration x Time - Example: Water flows into a cylindrical beaker at a constant rate. The base area of the beaker is 24 cm2. The water level raises by 10 cm every second. How quickly will the water level rise in the beaker with a base area of 30cm2?
Sol: The flow of the water in the beaker = 24 cm2 x 10 cm/s = 240 cm3/s
The base area is 30cm2 then the rate of water level rise will be 240/30 = 8 cm/s
Speed, Time and Distance Formulae
Some important speed, distance and time formulas are given below:
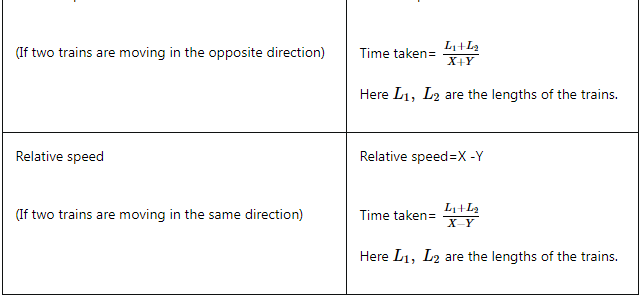
Some additional formulas of speed, distance and time are:
- If the ratio of the speeds of P and Q is p: q, then the ratio of the times used by them to reach the same distance is 1/p:1/q or q: p.
- If two individuals or automobiles or trains start at the exact time in the opposing direction from two points say A and B and after crossing each other they take time a and b respectively to finish the journey then the speed ratio is provided by the formula:
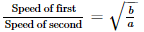
- If two individuals with two different speeds x and y cover the same distance and travel in opposite directions. Where the total time is given and distance is asked then the formula is:
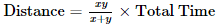
Types of Questions from Speed, Time and Distance
There are some specific types of questions from speed, time and distance that usually come in exams. Some of the important types of questions from speed, distance and time are as follows.1. Trains
- In the case of the train problems, the distance to be covered when crossing an object is equal to the distance to be covered = Length of train + Length of object.
- In case the object under consideration is a pole or a person or a point, we can consider them to be point objects with zero length. It means that we will not consider the lengths of these objects. However, if the object under consideration is a platform (non-point object), then its length will be added to the formula of the distance to be covered.
a) 112 km
b) 118 km
c) 120 km
d) None of these
Sol: Option 'a' is correctExplanation: Distance between A-B , A-C, C-B is 180, 120 and 60 km respectively.
Let x be the distance from A where the 2 trains meet.
According to given condition we haveSolving the equation we get x around 112 km.
2. Boats and Streams
- When the boat and the river's stream (or current) move in the same direction, the boat's relative speed is the sum of the speeds of the boat and the river. This is what is called "downstream speed."
- When the boat goes against the flow of the river, or in the opposite way, its speed is the difference between its speed and the speed of the stream. It's called "upstream speed."
Let B be the speed of the boat in still water and C be the speed of the river current.
If B>C;
Downstream Speed D = (B + C)
Upstream Speed U = (B – C)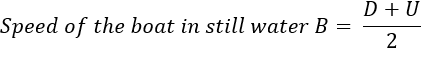
When the distance a boat travels upstream (against the flow of water) is the same as the distance it travels downstream (with the flow of water), then,
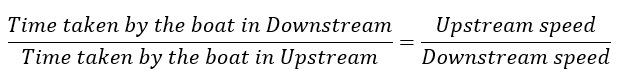
Example: Two boats, travelling at 5 km/h and 10 km/h, head directly towards each other. They begin at a distance of 20 km from each other. How far apart are they (in km) one minute before they collide?
(a) 1/12
(b) 1/6
(c) 1/4
(d) 1/3
Sol: Option 'C' is correct.
Explanation: Just before the collision, in the final minute.
Boat number 1 travelled = 5 x 1/60 = 1/12 km
Boat number 2 travelled = 10 x 1/60 = 1/6 km
As they move in opposite directions,
distance between the boats one minute before the collision is
1/12 + 1/6 = 1/4 km
3. Races
(i) Startup or headstart - When a runner lets another runner stay ahead of them in the same race, this is called a startup in the race.
(ii) Dead heat - When two or more runners cross the finish line at the same time, they are considered to have "finished" the race in a "dead heat."
Some More Useful Concepts
- When it is said that A can give B a start of x metres in a race of y meters, it means that in the same amount of time, B runs x metres less than A.
- In a race of y meters, if A beats B by t seconds, B is the loser and A is the winner. When A crosses the finish line, B is still a ways behind A. So, it takes B t seconds to go the rest of the way. So, we can figure out how fast loser (B) is going.
- Throughout the race there is always a certain relationship among runners i.e., they always maintain the ratio of speeds.
Example: In a race of 200 m, A beats S by 20 m and N by 40 m. If S and N are running a race of 100 m with exactly the same speed as before, then by how many metres will S beat N?
(a) 11.11 m
(b) 10 m
(c) 12 m
(d) 25 m
Sol: Option 'a' is correct.
Explanation: In the time that A takes to run 200 m, S runs 180 m and N runs 160 m. So, in the time
S takes to run 200 m, N runs 200 (160/180) =177.77 m or is beaten by 22.22 m.
So, in 100 m, N is beaten by 11.11 m.
4. Circular Motion
When the entities are moving in opposite directions, their relative velocity equals the sum of their individual velocities.When two objects are travelling in the same direction, the speed between them is equal to the difference in their absolute speeds.First MeetingLet A and B be two runners
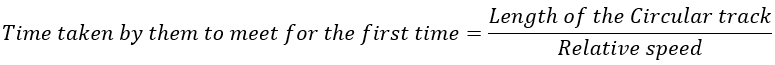
If A is the quickest runner and A meets B after tAB hours, A meets C after tAC hours, A meets D after tAD seconds/hours, etc., then A has met all the other runners for the first time. The LCM of the times it takes for A, B, C, D, etc. to finally meet for the first time is tAB.
First Meeting at the Starting Point
Assume that runner A is the quickest of all the runners and that he or she will meet runner B for the first time in tAB hours, runner C for the first time in tAC hours, runner D for the first time in tAD seconds/hours, and so on. The LCM of tAB, tAC, tAD, etc. is the time it takes
for all of them to meet for the first time.
Example: Ashish and Sagar are moving together on a circular track in opposite directions with speeds 15 m/s and 25m/s respectively. The length of the track is 600m When will they meet for the first time and when will they meet at the starting point for the first time?
Sol: Time taken to meet each other for the first time= Circumference/Relative speed
= 600/(15+25) = 600/40 = 15 seconds
Time taken by Ashish to complete one round = 600/15 = 40 seconds
Time taken by Sunil to complete one round = 600/25 = 24 seconds
Time when they meet for the first time at the starting point = LCM (40,24) = 120 seconds
Tips and Tricks to Solve Questions based on Speed, Time and Distance
Students can find different tips and tricks below for solving the questions based on speed, time and distance.
Tip 1: Relative speed is defined as the speed of a moving body with respect to another body. The possible cases of relative motion are, same direction, when two bodies are moving in the same direction, the relative speed is the difference between their speeds and is always expressed as a positive value. On the other hand, the opposite direction is when two bodies are moving in the opposite direction, the relative speed is the sum of their speeds.
Tip 2: Average speed = Total Distance / Total Time
Tip 3: When a train passes a moving man/point object, the distance travelled by train while passing it will be equal to the length of the train and relative speed will be taken as:
1) If both are moving in same direction then relative speed = Difference of both speeds
2) If both are moving in opposite direction then relative speed = Addition of both speeds
Tip 4: Train Passing a long object or platform, when a train passes a platform or a long object, the distance travelled by the train, while crossing that object will be equal to the sum of the length of the train and length of that object.
Tip 5: Train passing a man or point object, when a train passes a man/object, the distance travelled by the train while passing that object, will be equal to the length of the train.
Solved Examples of Speed, Time and Distance
Example 1: The speed of three cars are in the ratio 5 : 4 : 6. The ratio between the time taken by them to travel the same distance is
Sol: Ratio of time taken = ⅕ : ¼ : ⅙ = 12 : 15 : 10
Example 2: A truck covers a distance of 1200 km in 40 hours. What is the average speed of the truck?
Sol: Average speed = Total distance travelled/Total time taken
⇒ Average speed = 1200/40
∴ Average speed = 30 km/hr
Example 3: A man can go up a moving down escalator in 60 seconds. If escalator is moving at 2 steps/sec and speed of the person is 3 steps/sec on stationery escalator, find the time required by the man to go up when the escalator is not moving.
Sol: Let the number of steps be 'N'.
∴ Effective speed of man while going up = (3 - 2)
= 1 step/sec
= N/1 = 60
∴ N = 60 steps
Now, time taken by the man to go up when the escalator is not moving = 60/3
= 20 seconds
Example 4: Rahul goes Delhi to Pune at a speed of 50 km/h and comes back at a speed of 75 km/h. Find his average speed of the journey
Sol: Distance is same both cases
⇒ Required average speed = (2 × 50 × 75)/(50 + 75) = 7500/125 = 60 km/hr
Example 5: Determine the length of train A if it crosses a pole at 60km/h in 30 sec.
Sol: Given, speed of the train = 60 km/h
⇒ Speed = 60 × 5/18 m/s = 50/3 m/s
Given, time taken by train A to cross the pole = 30 s
The distance covered in crossing the pole will be equal to the length of the train.
⇒ Distance = Speed × Time
⇒ Distance = 50/3 × 30 = 500 m
Example 6: A 150 m long train crosses a 270 m long platform in 15 sec. How much time will it take to cross a platform of 186 m?
Sol: In crossing a 270 m long platform,
Total distance covered by train = 150 + 270 = 420 m
Speed of train = total distance covered/time taken = 420/15 = 28 m/sec In crossing a 186 m long platform,
Total distance covered by train = 150 + 186 = 336 m
∴ Time taken by train = distance covered/speed of train = 336/28 = 12 sec.
Example 7: Two trains are moving in the same direction at speeds of 43 km/h and 51 km/h respectively. The time taken by the faster train to cross a man sitting in the slower train is 72 seconds. What is the length (in metres) of the faster train?
Sol: Given: The speed of 2 trains = 43 km/hr and 51 km/hr Relative velocity of both trains = (51 – 43) km/hr = 8 km/hr Relative velocity in m/s = 8 × (5/18) m/s
⇒ Distance covered by the train in 72 sec = 8 × (5/18) × 72 = 160 Hence, the length of faster train = 160 m
Example 8: How long will a train 100m long travelling at 72km/h take to overtake another train 200m long travelling at 54km/h in the same direction?
Sol: Relative speed = 72 – 54 km/h (as both are travelling in the same direction)
= 18 km/hr = 18 × 10/36 m/s = 5 m/s
Also, distance covered by the train to overtake the train = 100 m + 200 m = 300 m Hence,
Time taken = distance/speed = 300/5 = 60 sec
Example 9: A boat takes 40 minutes to travel 20 km downstream. If the speed of the stream is 2.5 km/hr, how much more time will it take to return back?
Sol: Time taken downstream = 40 min = 40/60 = 2/3 hrs. Downstream speed = 20/ (2/3) = 30 km/hr.
As we know, speed of stream = 1/2 × (Downstream speed – Upstream speed)
⇒ Upstream speed = 30 – 2 × 2.5 = 30 – 5 = 25 km/hr.
Time taken to return back = 20/25 = 0.8 hrs. = 0.8 × 60 = 48 min.
∴ The boat will take = 48 – 40 = 8 min. more to return back.
Example 10: A ship 156 km from the shore springs a leak which admits 2.5 metric tons of water in 13/2 minutes. A quantity of 68 metric tons would suffice to sink it, but the pumps can throw out 15 metric tons in an hour. The average rate of sailing so that it just reaches the shore as it begins to sink should be
a. 18 kmph
b. 60 kmph
c. 15 kmph
d. 10 kmph
Sol: Option 'a' is correct
Explanation: In one minute, amount flowing in = 15/39 MT
In one minute, amount thrown out = 15/60 = 1/4 MT
Effective rate of filling in one hour= (15/39 - 1/4) MT = 21/56 MT/min
Time till it just begins to sink = (68 x 156)/21 = 505 min
Speed required = (156/505) = 0.3 km/min = 0.3 x 60 km/hr = 18 km/hr.
Example 11: have to be at a certain place at a certain time and find that I shall be 40 minutes late, if I walk at the rate of 4 kmph and 40 min early if I walk at the rate of 5 kmph. What is the usual time required by me to reach my destination?
a. 7 hrs
b. 14 hrs
c. 6 hrs
d. 3.5 hrs
Sol: Option 'b' is correct
Explanation: Let t be the usual time.
:. Distance covered D = 4 x (t + 2/3) = 5 x (t-2/3)
after solving , we get t = 6
Example 12: A railway passenger counts the telegraph posts as he passes them. If they are 50 metres apart and the train is going at 48 kmph, how many posts will he pass per minute?
a. 16
b. 20
c. 24
d. 10
Sol: Option 'a' is correct
Explanation: 48 km/hr = 48 x 5/18 m/sec
= (49 x 5 x 60)/ 18
Number of posts = 800/50 = 16.
|
184 videos|131 docs|110 tests
|
FAQs on Speed, Distance & Time Important Notes - Quantitative Aptitude (Quant) - CAT
| 1. What is the formula to calculate speed, distance, and time? |  |
| 2. How do you convert speed from kilometers per hour (km/h) to meters per second (m/s)? | |
| 3. What are some common applications of speed, time, and distance in real life? | |
| 4. Can you explain the concept of acceleration in relation to speed and time? | |
| 5. What are some tips and tricks to solve speed, time, and distance problems quickly? | |
|
4.86/5 Rating |
|
Oct 27, 2024 Last updated |
|
Explore Courses for CAT exam
|
|
Sample Paper
,mock tests for examination
,Important questions
,Distance & Time Important Notes | Quantitative Aptitude (Quant) - CAT
,practice quizzes
,ppt
,Speed
,Distance & Time Important Notes | Quantitative Aptitude (Quant) - CAT
,video lectures
,MCQs
,study material
,Free
,Objective type Questions
,Distance & Time Important Notes | Quantitative Aptitude (Quant) - CAT
,Summary
,Viva Questions
,Speed
,past year papers
,shortcuts and tricks
,Semester Notes
,Previous Year Questions with Solutions
,Extra Questions
,Exam
,Speed
;
Important Notes: Speed, Distance & Time Free PDF Download
Importance of Important Notes: Speed, Distance & Time
Important Notes: Speed, Distance & Time
Important Notes: Speed, Distance & Time CAT Questions
Study Important Notes: Speed, Distance & Time on the App
|
© EduRev
|
Education Revolution
|
Follow Us
|
