| Table of contents |

|
| Branches of Geometry |

|
| Dimensions of Geometry |

|
| Two-Dimensional Geometry |

|
| Measurement in Geometry |

|
Branches of Geometry
Let us start the discussion with the different branches of geometry and learn about each of them.
- Euclidean Geometry: Euclid’s geometry or the Euclidean Geometry deals with the study of geometrical shapes both two-dimensional and three-dimensional, along with the relation between these figures in terms of lines, and angles, congruence points, and surfaces. Euclid’s book on elements gave an introduction to axioms and different postulates for solid & plane figures that helped in describing geometric shapes.
- Non-Euclidean Geometry: As the name suggests, it is the branch of geometry that includes everything that does not fall under Euclidean geometry. It is also known as spherical geometry and hyperbolic geometry.
- Algebraic Geometry: It is a branch of geometry which deals with curves or surfaces and includes linear & polynomial algebraic equations that are used for solving the sets of zeros.
- Projective Geometry: Projective geometry is a branch of geometry that deals with the connections between geometric shapes that are a result of the projection of the object onto another surface.
- Discrete Geometry or Combinatorial Geometry: It is something that relates to the study of geometric objects which are discrete by nature such as lines, triangles, points, circles etc.
- Differential Geometry: It is related to general relativity in physics and uses algebra techniques and calculus for solving problems.
- Topology: It deals with the properties of space under continuous mapping. It has applications in various fields such as metric spaces, initial & final structure, continuity, proximal continuity, proximal spaces etc.
Dimensions of Geometry
In the previous header we saw the geometry basics branches, let us now understand the different dimensions of geometry in mathematics. In mathematics, objects can be categorised into no dimension objects, one-dimensional, two-dimensional and three-dimensional objects.
Non-Dimensional Geometry
A point can be visualised as a single spot or a place on a plane. It is usually specified by a dot that has no real size or shape. Hence point geometry has no dimension or we can say that it has the only position.
One Dimensional Geometry
The line is straight and the briefest distance between two points. That is we can say that the number of points when connected makes a line geometry. As lines only possess length and no width, therefore it is counted in one-dimensional shapes/objects. The different types and terms related to lines are as follows:
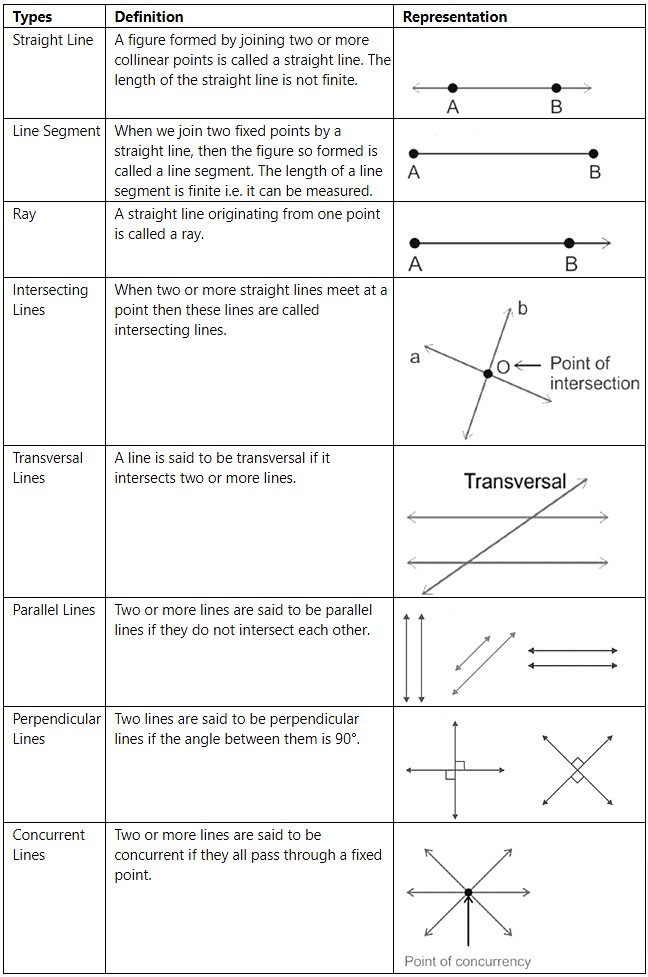
Angles and Types of Angles in Geometry
When two rays originate from a fixed point, then the amount of rotation from one ray to another ray is called the angle between the rays or the angle between lines. The rays are called arms of the angle. Angles are generally measured in degrees or radians. The different types of geometry angles with their definition and representation are as follows:
Two-Dimensional Geometry
Plane geometry or two-dimensional geometry includes flat figures like circles, rectangles, triangles and other polygons. The two-dimensional objects can be drawn on paper and they hold both length and width. The different two-dimensional objects with definitions and images are as follows:
Polygons
A polygon in maths is said to be a two-dimensional shape. There are different names as per the sides:
- Triangle: a polygon formed by three line segments.
- Quadrilateral: a polygon formed by four line segments.
Similarly, there are different other types of polygons. Refer to the below image for the same.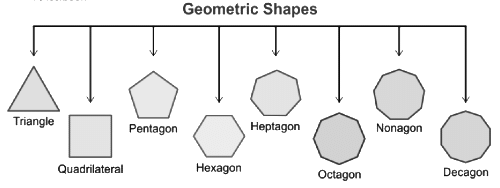
Triangle
A triangle is a polygon with 3 vertices say P, Q, and R which is represented as △PQR. The different types of triangles are listed in the below table.
Types of Triangles based on the Sides
Triangle can be classified into the following groups on the basis of the side of the triangle.
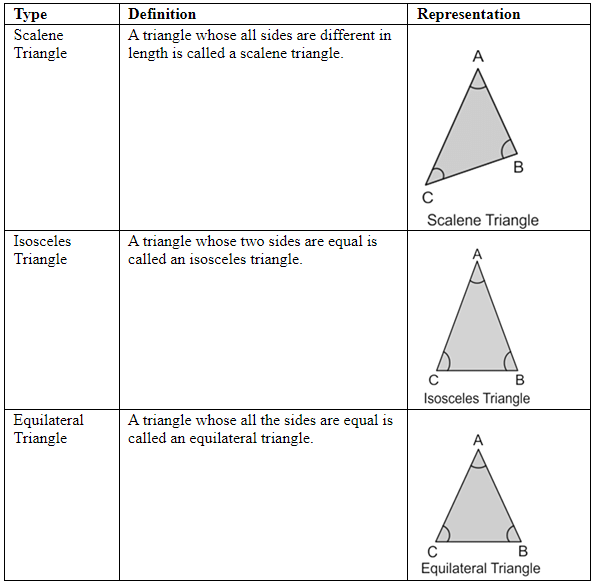
Types of Triangles based on the Angles
Triangles in geometry can also be classified into the following groups on the basis of the measurement of the angle of a triangle.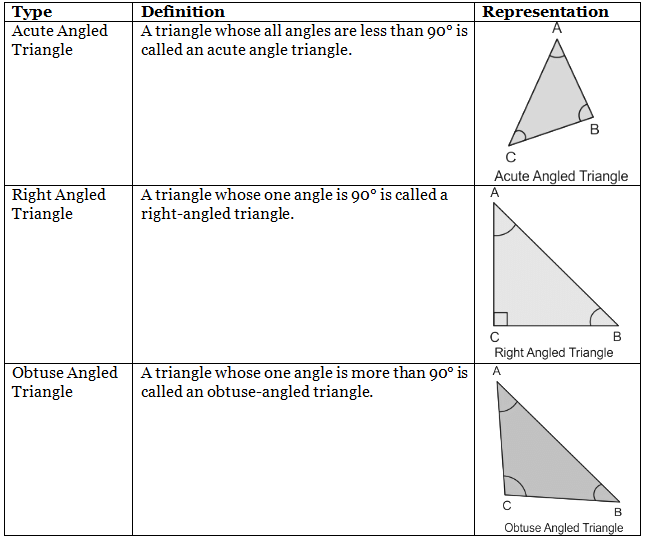
Quadrilaterals
A figure formed by a four-line segment is called a quadrilateral. The sum of angles of any quadrilateral is 360°. That is if the four angles of a quadrilateral are ∠A, ∠B, ∠C, ∠D. Then ∠A + ∠B + ∠C + ∠D = 360°.
The different types of quadrilaterals are listed in the below table.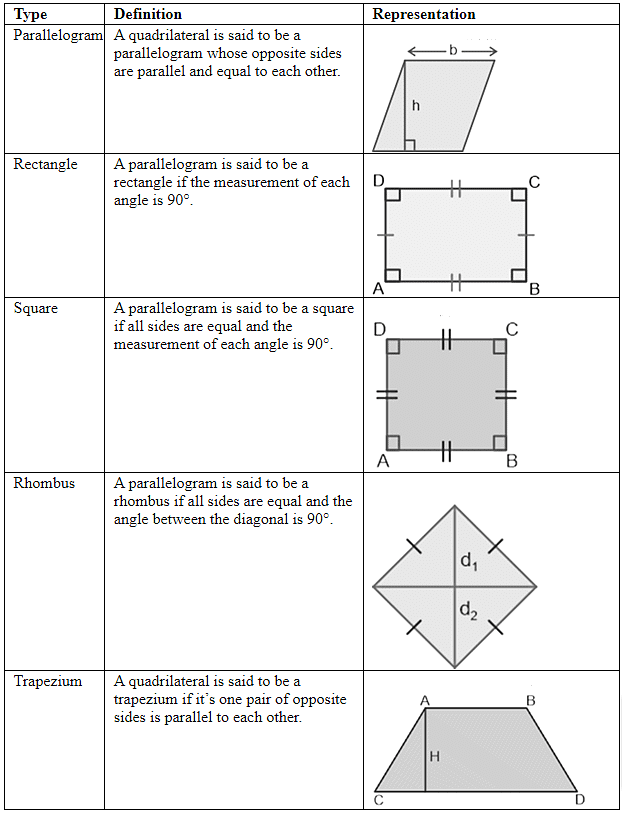
The other types of polygons are:
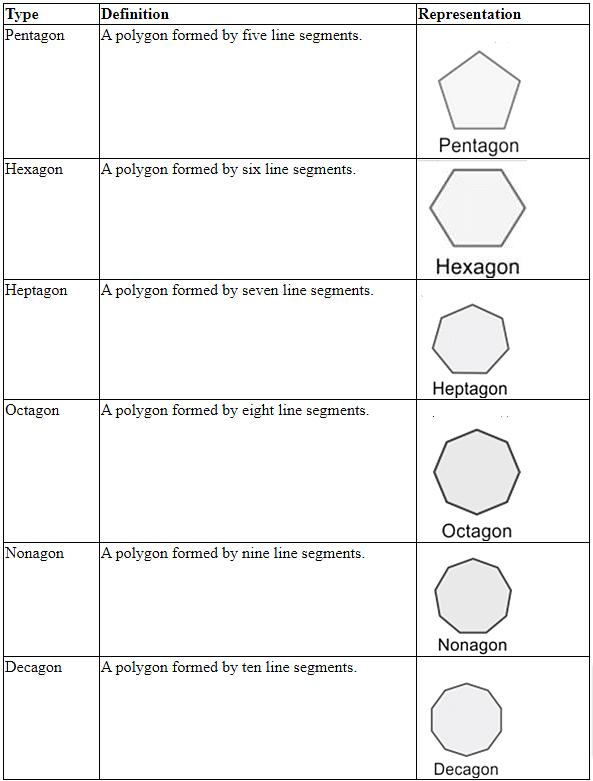
Circles
It is the locus of all the points which lie in a plane such that their distances from a fixed point are always constant. The fixed point is called the center of the circle. A circle of center O and radius r is shown below.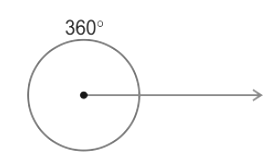
The different parts of a circle are listed below: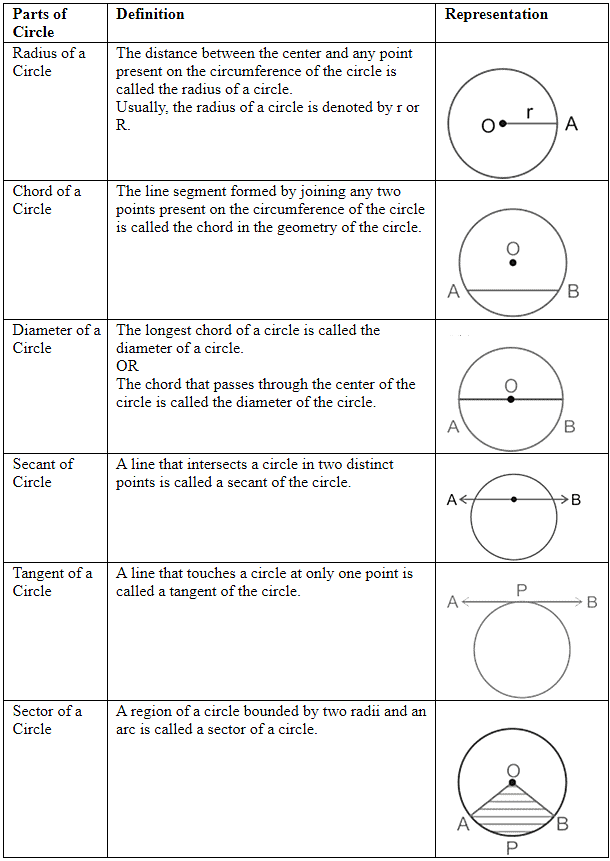
Three-Dimensional Geometry
Solid geometry or three-dimensional geometry includes objects like cubes, cuboids, prisms, cylinders, cones and spheres. All these objects hold a length, width, and height. The important characteristics of solid geometry are edges, faces and vertices. Let us understand each of them in detail.
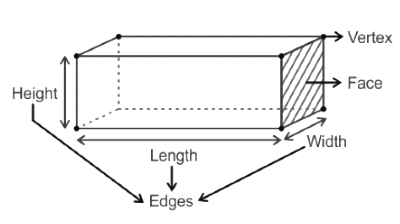
Edges
Edges in a 3D shape join one corner point to another corner point. That is it is the line segment on the boundary that connects one vertex to the other one. They serve as the junction of two faces.
Faces
A face for 3D objects refers to the flat or curved surface of an object. For a 3D object, the face is in 2D format. A particular shape can have multiple faces.
Vertices
A point in 3D objects where two or more lines meet is said to be the vertex. Or one can understand vertices as the point of intersection of edges.
Measurement in Geometry
So far we read about the geometry definition, different branches, dimensions and related shapes with their images. Let us now understand the geometry formulas under the header measurement in geometry. This involved formula for the length, area, perimeter and volume calculation of different objects.
Measurement in Two-Dimensional Geometry
The area and perimeter are determined using the length and bread of different geometrical objects. Some of the important geometry symbols formulas related to 2D are listed below.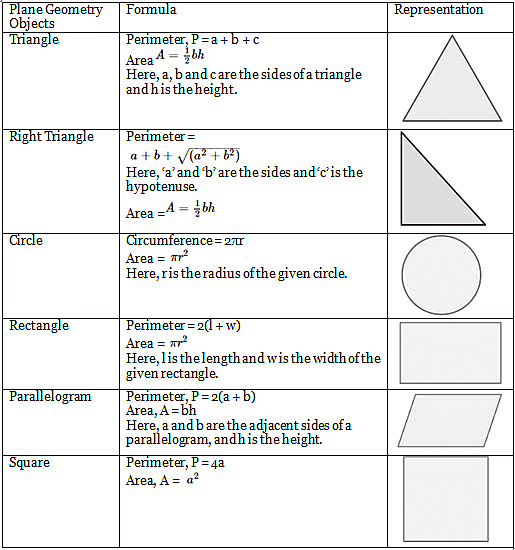
Analytic geometry in two-dimensional deals with the section formula, distance formula, the centroid of a triangle, the midpoint formula and so on. All these are determined using knowledge of coordinate geometry concepts.
Similarity and Congruency in Geometry
When two figures hold an identical shape or an equal angle but do not have the same size are said to be similar. If two figures have the same shape and size, then they are said to be congruent.
Measurement in Three-Dimensional Geometry
The three-dimensional geometry objects or shapes as per the name are represented using 3 coordinates namely x, y and z. The formula of some important and relevant solid geometry are listed below.
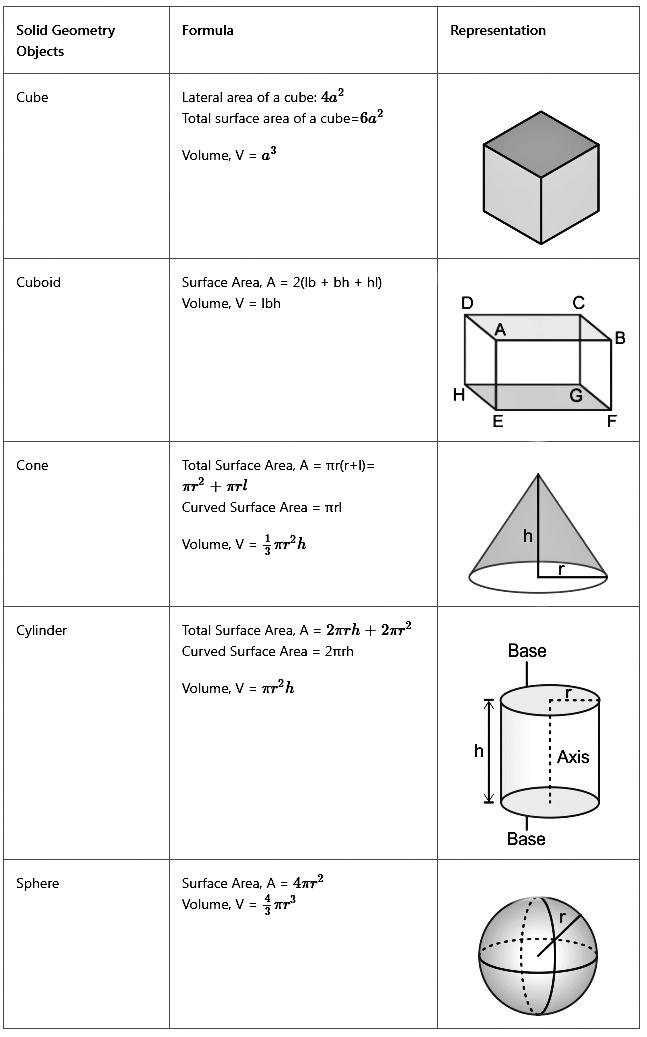
Some other related concepts of solid geometry are listed below.
Direction Cosines of a Line
If a directed line say ‘R’ departing through the origin creates angles α, β and γ with x, y and z-axes, respectively, then the cosine of these angles, i.e., cos α, cos β and cos γ is termed as direction cosines of the given directed line ’R’. Direction cosines of the line joining two points: P(x1,y1,z1) and Q(x2,y2,z2) is given by the formula:
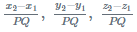
Direction Ratios of a Line
The directional ratios of a given line are the digits or numbers that are proportional to the direct cosines of that line. If a, b, c as the direction ratios of a line and l, m and n be the direction cosines then: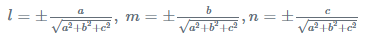
Equation of Line in 3-D Geometry
If l, m, n are the direction cosines of a line passing through the point (x1,y1,z1), then the equation of the line is as follows: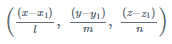
The equation of a line passing through the two points say; (x1,y1,z1) and (x2,y2,z2). Then the equation of the line is given by the formula: 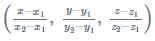
Angle Between Two Lines
The angle θ between two lines whose direction ratios are proportional to a1,b1,c1 and a2,b2,c2 respectively is given the formula: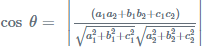
FAQs on Overview: Geometry - CAT
| 1. What is two-dimensional geometry? |  |
| 2. What are the main branches of geometry? |  |
| 3. What are some examples of two-dimensional shapes? |  |
| 4. What are the properties of two-dimensional shapes? |  |
| 5. How is two-dimensional geometry used in real life? |  |














