Overview: Matrix | General Intelligence and Reasoning for SSC CGL PDF Download
Introduction
An m × n matrix is usually written as: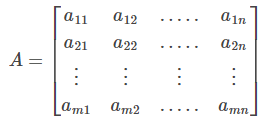
In brief, the above matrix is represented by A = [aij] mxn. The numbers a11, a12, ….. etc., are known as the elements of the matrix A, where aij belongs to the ith row and jth column and is called the (i, j)th element of the matrix A = [aij].
Important Formulas for Matrices
If A and B are square matrices of order n, and In is a corresponding unit matrix, then
(a) A(adj.A) = | A | In = (adj A) A
(b) | adj A | = | A |n-1 (Thus A (adj A) is always a scalar matrix)
(c) adj (adj.A) = | A |n-2 A
(d) 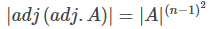
(f) adj (Am) = (adj A)m,
(g) adj(kA) = kn-1 (adj.A), KϵR
(h) adj (In) = In
(i) adj 0 = 0
(j) A is symmetric ⇒adj A is also symmetric
(k) A is diagonal ⇒adj A is also diagonal
(l) A is triangular ⇒adj A is also triangular
(m) A is singular ⇒| adj A | = 0
Types of Matrices
(i) Symmetric matrix: A square matrix A = [aij] is called a symmetric matrix if aij = aji, for all i, j.
(ii) Skew-symmetric matrix: when aij = – aji
(iii) Hermitian and skew – Hermitian matrix: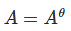
(Hermitian matrix)(Aθ represents conjugate transpose)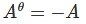
(skew-Hermitian matrix)
(iv) Orthogonal matrix: if AAT = In = ATA
(v) Idempotent matrix: if A2 = A
(vi) Involuntary matrix: if A2 = I or A-1 = A
(vii) Nilpotent matrix: A square matrix A is nilpotent; if Ap = 0, p is an integer.
Trace of Matrix
The trace of a square matrix is the sum of the elements on the main diagonal.
(i) tr(λA_ = λ tr(A)
(ii) tr(A + B) = tr(A) + tr(B)
(iii) tr(AB) = tr(BA)
Matrix Transpose
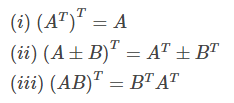

Properties of Matrix Multiplication
(i) AB ≠ BA
(ii) (AB)C = A(BC)
(iii) A.(B + C) = A.B + A.C
 |
Test: Matrix
|
Start Test |
Adjoint of a Matrix

Inverse of a Matrix
A-1 exists if A is non-singular, i.e.,
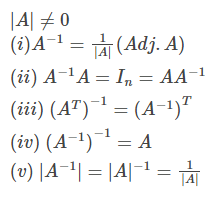
Order of a Matrix
A matrix which has m rows and n columns is called a matrix of order m x n.
For example, the order of
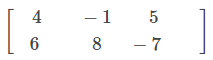
matrix is 2 x 3.
Note: (a) The matrix is just an arrangement of certain quantities.
(b) The elements of a matrix may be real or complex numbers. If all the elements of a matrix are real, then the matrix is called a real matrix.
(c) An m x n matrix has m.n elements.
Illustration 1: Construct a 3×4 matrix A = [aij], whose elements are given by aij = 2i + 3j.
Sol: In this problem, I and j are the number of rows and columns, respectively. By substituting the respective values of rows and columns in aij = 2i + 3j, we can construct the required matrix.
Given aij = 2i + 3j
so a11 = 2+3 = 5, a12 = 2+6 = 8
so a11 = 2+3 = 5, a12 = 2+6 = 8
Similarly, a13 = 11, a14=14, a21 = 7, a22=10, a23=13, a24=16,a31=9, a32=12, a33=15, a34=18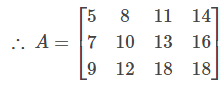
Illustration 2: Construct a 3 x 4 matrix, whose elements are given by: aij =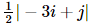
Sol: The method for solving this problem is the same as in the above problem.
Since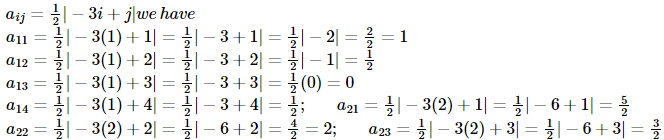
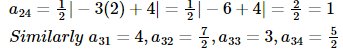
Hence, the required matrix is given by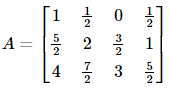
Trace of a Matrix
Let A = [aij]nxn and B = [bij]nxn and λ be a scalar,
(i) tr(λA) = λ tr(A) (ii) tr(A + B) = tr(A) + tr(B) (iii) tr(AB) = tr(BA)
Transpose of Matrix
The matrix obtained from a given matrix A by changing its rows into columns or columns into rows is called the transpose of matrix A and is denoted by AT or A’. From the definition, it is obvious that if the order of A is m x n, then the order of AT becomes n x m; For example, transpose of a matrix.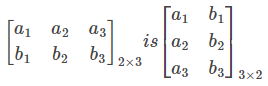
 |
Download the notes
Overview: Matrix
|
Download as PDF |
Properties of Transpose of Matrix
(i) (AT)T= A
(ii) (A + B)T = AT+ BT
(iii) (AB)T = BTAT
(iv) (kA)T = k(A)T
(v) (A1A2A3 ……An-1An)T =
(vi) IT = I (vii) tr(A) = tr(AT)
Problems on Matrices
Illustration 3: If 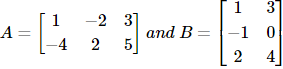 . then prove that (AB)T = BTAT.
. then prove that (AB)T = BTAT.
Solution: By obtaining the transpose of AB, i.e., (AB)T and multiplying BT and AT, we can easily get the result.
Here, AB =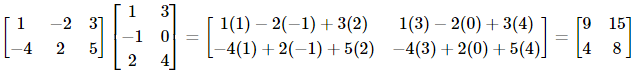
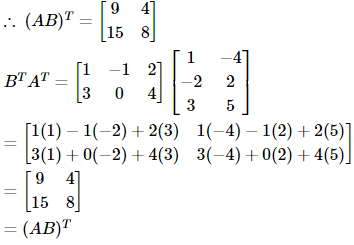
Illustration 4: If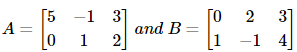 Then what is (B’)’A’ equal to?
Then what is (B’)’A’ equal to?
Sol: In this problem, we use the properties of the transpose of a matrix to get the required result.
We have =
|
177 videos|129 docs|197 tests
|
FAQs on Overview: Matrix - General Intelligence and Reasoning for SSC CGL
| 1. What is a matrix? |  |
| 2. How do you add two matrices together? |  |
| 3. What is the determinant of a matrix? |  |
| 4. How do you multiply two matrices together? |  |
| 5. What is the inverse of a matrix? |  |






















