Overview: Permutations and Combinations | Quantitative Aptitude (Quant) - CAT PDF Download
Permutation and Combination
Permutation and combination provide ways to represent a certain group of objects by choosing them in a set and creating subsets.
Maths permutations and combinations, in general, allow several methods to arrange a certain collection of data. Now comes the question: what is the definition of permutations and combination? When there is a selection of an object or data from a certain group of data then it is said to be a combination, whereas with the selection of data when the order of data comes into consideration then it is called permutations.
With this article on Permutation and combination learn more about permutation and combination formulas with solved examples, definitions, permutation vs combination table and more.
There is one more concept that is the repetition of data, both Permutation, and combination are divided into with repetition and without repetition and both concepts are very important in Mathematics. Will go through all such concepts in the article itself.
Factorial
The continued product of first n natural numbers is denoted by n! i.e
n! = 1 × 2 × 3 × ……. × n
Points to Remember
Key Points regarding factorial notation:
- 0! = 1
- Factorial of negative(-ve) figures and fractions is not specified.
n!/r! = n(n−1)(n−2)……..(r+1)
The Fundamental Principle of Multiplication
Let us assume there are two assignments A and B such that task A can be done in m different ways following which the second task B can be done in n different ways. Then the number of ways to accomplish the task A and B in succession respectively is given by m × n ways.
The Fundamental Principle of Addition
Let us assume there are two tasks A and B such that task A can be done in m different styles and assignment B can be completed in n ways. Then the number of ways to complete either of the two tasks is given by (m + n) ways.
Permutation Formula
Let us suppose there are 3 stools/chairs A, B, and C. So, the number of ways in which these chairs can be arranged is given by 3! = 6, wherein individual arrangement matters, and these arrangements are ABC, ACB, BCA, BAC, CAB, and CBA.
Mathematically, the permutation is associated with the act of arranging all the data of a set into some sequence or order. Permutations come into account in more or less almost every domain of mathematics. The permutation formula is as follows:
- Consider r and n to be positive integers such that 0 ≤ r ≤ n. Then the number of ways to arrange “r” thing taken at a time out of n distinct things is given by:
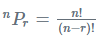
- The number of methods to arrange n distinct things taken all at a time is given by:
nPn = n! - The number of ways to arrange “r” things taken at a time out of n different things, wherein each thing may be repeated any number of times is given by:
nr
There are two types of permutation:
Repetition is Allowed
These are the simplest to determine.
Consider when a piece has n different types and one has r choices each time then the permutations is defined by:
n × n × … (r times)
This implies there are n possibilities for the first selection, followed by n possibilities for the second selection, and so on, multiplying each time.
No Repetition
In this case, each time the number of choices is reduced. Consider when a piece has n different types and one has r choices each time without repetition the permutations are:
n × (n-1) × (n-2)…
This implies there are n possibilities for the first selection, followed by n-1 possibilities for the second selection, and so on, multiplying each time.
Derivation of Permutation Formula
Let us consider that there are r cartons and each of them can carry one thing. There will be as many permutations as there are methods of filling in r empty carton by n things.
- Number of ways the first carton can be filled: n
- Number of ways the second carton can be filled: (n – 1)
- Number of ways the third carton can be filled: (n – 2)
- Number of ways the fourth carton can be filled: (n – 3)
- Number of ways rth carton can be filled: [n – (r – 1)]
- The number of permutations of n distinct things taken r at a time, where 0 < r ≤ n and the objects do not replicate is: n(n – 1)(n – 2)(n – 3) . . . (n – r + 1)
⇒ nPr = n(n–1)(n–2)(n–3)...(n–r+1)
Multiplying and dividing by (n – r) (n – r – 1) . . . 3 × 2 × 1, we receive: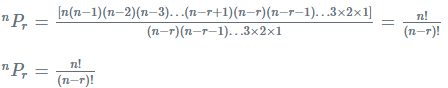
Circular Permutation
So far the type of permutation we studied is a straight permutation, the next is Circular Permutation. In this type of permutation, the number of ways to arrange n distinct things is given by: (n – 1)!
The number of ways to arrange n distinct things but all of them looks identical in a circular arrangement like the arrangement of beads in a necklace or the arrangement of flowers in a garland is given by: (n – 1)!/2
Now, let’s move towards the concept of combination;
Combination Formula
In combination, we have to select r things out of n given things wherein r ≤ n. So, the order in which we select these are things of the given n things does not matter. So, the number of ways to select r things out of n given things wherein r ≤ n is given by the below combination formula: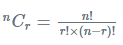
The combination is also classified as repetition allowed and repetition not allowed.
Key point:
The difference between permutation and combination is that permutation is all about the arrangement of things whereas combination is about selection where arrangement does not matter.
Derivation of Combination Formula
Let us consider that there are r cartons and all of them can carry one object.
- Number of ways to choose the first article/element from n distinct objects: n
- Number of ways to select the second object/element from (n-1) distinct objects: (n-1)
- Number of ways to select the third object/element from (n-2) distinct objects: (n-2)
- Number of ways to select rth object/element from [n-(r-1)] different objects: [n-(r-1)]
- Completing the selection of r elements from the primary set of n things formulates an ordered subset of r elements.
∴ The number of ways to make a selection of r elements of the original or initial set of n elements is: n (n – 1) (n – 2) (n-3) . . . (n – (r – 1)) or n (n – 1) (n – 2) … (n – r + 1).
Let us suppose the ordered subset of r elements and all their permutations. Then the total estimate of all permutations of this subset is equivalent to r! because r objects in each combination can be ordered in r! ways.
Therefore, the total number of permutations of n distinct elements taken r at a time is nCr × r!. It is nothing but:
Relation Between Permutation and Combination
As we know, the number of ways to arrange things taken at a time out of n different things is given by: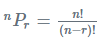
Whereas, the number of ways to select r things out of n given things wherein r ≤ n is given by: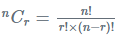
So from these two definitions, we can conclude that the relation between permutation and combination is as follows:
nPr = r! × nCr
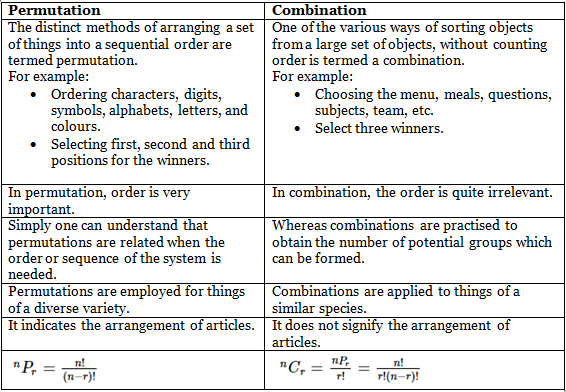
Difference Between Permutation and Combination
The difference between permutations and combinations can be surmised by understanding the different conditions where the permutations and combinations theories are applied.
For grouping of articles/elements, or to arrange a count of the number of subgroups that can be reached from the provided set of things, we practice combinations. Moreover, to determine the number of possible arrangements of dissimilar elements, we practice permutations
Permutation and Combination: Important Points
The following details would help us to compile the important points of the difference between permutation and combination.
- Permutations are used to obtain the count of the different number of arrangements that can be created with the given points.
- The combination is helpful to get the count of the number of distinct subgroups which can be developed from the provided larger set.
- For the identical values of n and r, the number of permutations or arrangements would always be larger than the number of combinations or groups.
- Seating arrangements for a related event or for official seating arrangements, the various possible seating arrangements can be determined by applying the formula of permutations.
- Furthermore, the different committees are created by selecting a few people, and the number of probabilities of building a committee is estimated by adopting the combinations formula.
Solved Examples
Example 1: How many five letter words (with or without meaning) can be formed such that the letters appearing in the odd positions are taken from the unrepeated letters of the word MATHEMATICS whereas the letters which occupy even places are taken from amongst the repeated letters of the same?
(a) 3600
(b) 540
(c) -150
(d) None of these
Ans: (b)
There are 3 odd places namely lst, 3rd and 5th which are to be filled by unrepeated 5 letters H. E. l, C. S. This can be done in 5P3 = 5 X 4 X 3 = 60 ways. We have two even places namely 2nd and 4th which is to be filled by repeated letters (2M. 2A, 2T) i.e., 6 letters. These two even places can be filled by 3 different types of letters as under.
(i) All different: 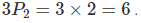
(ii) Both alike 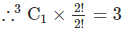
Thus even places can be filled in 6 + 3 = 9 ways. Hence by fundamental principle of counting. the required number of words is 60 x 9 = 540. Ans.(b)
Example 2: An entomologist noticed 15 ants crawling on his table. Exactly 13 of them were male and 2 were female. He noticed that they were crawling on the table in a random order such that no three of them were ever in the same straight line. Suddenly, three of the male ants start following one of the female ants such that, all four of them were in a single line. Then the maximum number of distinct straight lines that the entomologist can draw passing through any two ants is
(a) 56
(b) 44
(c) 105
(d) 100
Ans: (d)
Initially there were 15C2 = 105 lines. Now for the four ants among themselves the number of lines are decreased by (4C2 - 1) = 5 i.e., a net decrease of 5 lines i:e., there are 105 - 5 = 100 possible lines. Ans.(d)
Example 3: A train is going from Mumbai to Pune and makes S stops on the way. 3 persons enter the train after it has started from Mumbai with 3 different tickets. How many different sets of tickets they may have had?
(a) 15p3
(b) 3 × 15P3
(c) 15C3
(d) 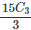
Ans: (c)
Since three persons entered the train after it has started from Mumbai, so they could have entered at:
1st station (from where they could have bought tickets for the2nd, 3rd, 4th or 5th stations or for Pune i.e. 5 tickets).
2nd station (from where they could have bought tickets for the 3rd, 4th for 5th stations or for Pune i.e. 4 tickets).
3rd station (form when: they could have bought tickets tor the 4th or 5th stations or tor Pune i.e. 3 tickets).
4th station from where they could have bought tickets tor the 5th station or for Pune i.e., 2 tickets)
5th station (from when: they could have bought a ticket for Pune i.e. 1 ticket)
Thus, we can see that there are 5+4+3+2+1= 15 tickets available out of which 3 tickets are to be selected. This can be done in 15C3 ways.
Example 4: Suppose a city has m parallel roads running East-West and n parallel roads running North-South. How many rectangles are formed with their sides along these roads?
(a) mn/4
(b) 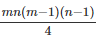
(c) 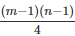
(d) None of these
Ans: (b)
To form a rectangle. we require two lines from East to West and two lines from North to South. Therefore, total number at rectangles which we can get is:
Example 5: Mohan, a thief, went to a liquor shop where he decided to take away 15 bottles. In the shop there are bottles of Wine, Whisky, Rum, Vodka and Gin. In how many ways he can select the bottles?
(a) 19C4
(b) 20C4
(c) 15C5
(d) 2200
Ans: (a)
As there is no restriction in choosing the bottles,
Therefore, By using the formula n+r−1Cr−1
= 15+5−1C5−1 = 19C4
|
167 videos|229 docs|95 tests
|
FAQs on Overview: Permutations and Combinations - Quantitative Aptitude (Quant) - CAT
| 1. What is the formula for calculating permutations? |  |
| 2. What is the formula for calculating combinations? |  |
| 3. What is the relation between permutation and combination? |  |
| 4. What is the difference between permutation and combination? |  |
| 5. What are some important points to consider in permutation and combination? |  |





















