Overview: Clocks | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Structure of a Clock |

|
| Angle equivalence of a minute |

|
| Speed of the hands |

|
| Comparison of Speed of hands |

|
Introduction
A Clock is a circular device provided with three hands viz. an hour hand, minute and second hand. The study of the clock is known as “horology”.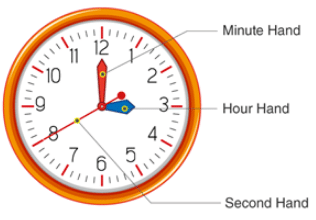 A basic structure of a clock with three hands
A basic structure of a clock with three hands
Structure of a Clock
A clock is composed of 360 degrees and divided into 12 equal divisions. The angle between the consecutive divisions is obtained by dividing the total angle of clock 360° by the number of divisions i.e. 12. Twelve equal divisions of a clockThe angle between any two consecutive divisions = (360°)/12= 30°
Twelve equal divisions of a clockThe angle between any two consecutive divisions = (360°)/12= 30°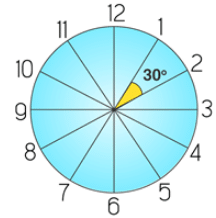 Angle divisions of a clockA close observation of a clock reveals that an angular space between any two consecutive divisions has further five more divisions. The area between the two divisions corresponds to a value of 5 minutes. Hence, dividing the 30° by five will result in the angular value of a minute.
Angle divisions of a clockA close observation of a clock reveals that an angular space between any two consecutive divisions has further five more divisions. The area between the two divisions corresponds to a value of 5 minutes. Hence, dividing the 30° by five will result in the angular value of a minute.
Angular value of a minute = (30°)/5= 6°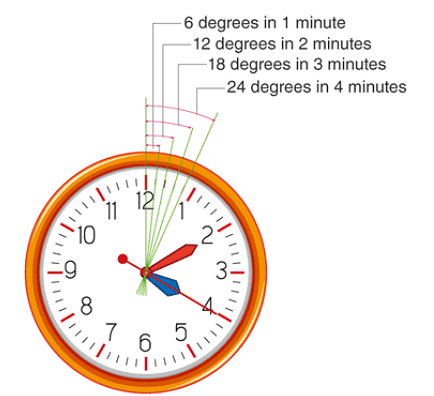 Angular values of minutes
Angular values of minutes
Angle equivalence of a minute
The table given below demonstrates the angular values of the first ten minutes: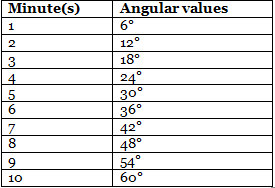
Speed of the hands
A clock has three hooks and all three move at different rates. The speed of moving object depends on the distance travelled and the time taken to cover a specific range.
The speed is calculated by:
Speed = Distance/(Time taken)
The speed of a minute hand:
A minute hand travels 360° in one hour. i.e. it travels through all the 12 divisions around the clock every hour. (1 hour = 60 minutes)
Speed of a minute hand = (360°)/(60 minutes)
Speed of a minute hand = 6° per minute.
The speed of an hour hand:
An hour hand travels 30° in an hour. i.e. it covers a distance of 5 minutes (the gap between consecutive divisions) in 60 minutes.
Speed of an hour hand = (30°)/(60 minutes)
Speed of an hour hand =1/2 ° per minute.
Comparison of Speed of hands
The difference in the speed = 6°– (1/2°) = 5.5° per minute
Comparing the speed of the minute hand and an hour hand, one can conclude that the minute hand is always faster than the hour hand by 5.5° or an hour hand is always slower than the minute hand by 5.5°
Note: The evaluation of the speed of second hands is not necessary as it travels a corresponding distance of 1 second in a second.
Frequency of coincidence and collision of hands of a clock:
As we know the hands of clock moves at different speeds, they coincide and collide and also make different angle formations among themselves at various times in a day.
Example 1: How many times in a day do the minute and hour hands of a clock coincide (Angle between them is zero) with each other? A first collision of the hands in a clock at midnightSol:
A first collision of the hands in a clock at midnightSol:
Logical explanation
A day starts at midnight, and hence the first-ever coinciding of hands happen at midnight. Now observing the clock, the next coincidence will occur at approximately 1’ o’clock and 5 minutes. Thus, one can conclude that every hour, there is one coincidence of hands. Therefore, the answer should be 24 times for 24 hours. But it is not the correct answer and right logic.
Now observe the time between 11 to 12, either it can either be A.M or P.M, the hands are not coinciding between 11’o o’clock and 12’o o’clock. The coinciding of hands at 12’ o clock is the coincidence between 12 and 1 and 11 and 12. Hence, in 12 hours, there will only be 11 coincidence, extending the logic for 24 hours of the day, there will be 22 coincidences.
If 12:0:0 A.M is the first coincidence of the hands in a day then the next collision will be at 1’o o’clock 5 minutes, but the evaluation of seconds is difficult, but not impossible.
Logical calculation
We know in 12 hours there will be 11 coincidences. Therefore, one collision will happen at:
Frequency of one collision = (12 hours)/11
Frequency of one collision = (12*60 mins)/11
Frequency of one collision = (720 mins)/11
Frequency of one collision = 65(5/11)
The value 65(5/11) indicates that the hands of a clock coincide after every 65 minutes 5/11 of a minute. i.e. if 12:0:0 is the first collision, then the exact time of the next collision will be obtained by adding 65(5/11) to 12 o’clock.
The below table denotes the time at which both the hands of a clock collide: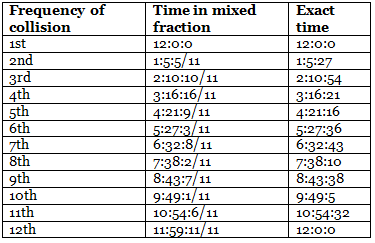
Finding the time when the angle is known
When the angle between the hands are not perfect angles like 180°, 90° or 270°, the solving of the questions becomes difficult and time-consuming at the same time. The logic below provides a trick to address problems involving angles of hands for other than standard aspects.
T = 2/11 [H*30±A]
Where:
- T stands for the time at which the angle formed.
- H stands for an hour, which is running.
(If the question is for the duration between 4 o’clock and 5 o’clock, it’s the 4th hour which is running hence the value of H will be ‘4’.)
- A stands for the angle at which the hands are at present.
(The value of A is provided in the question generally)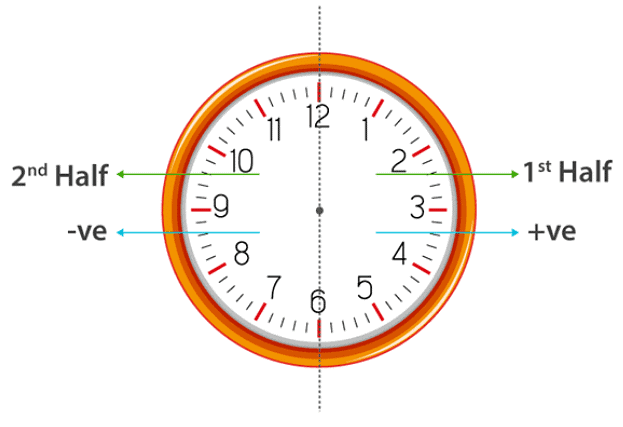 The clock is divided into two parts: 1st and 2nd half as shown above
The clock is divided into two parts: 1st and 2nd half as shown above
If the time given in the question lies in the first half, then the positive sign is considered while evaluating the time else, then the negative sign is used.
Example 2: At what time between 3 and 4 o’clock, the hands makes an angle of 10 degrees?
Sol:
Given: H = 3 , A = 10
Since both three and four lies in the first half considered a positive sign.
Calculations:
T = 2/11 [H*30±A]
T = 2/11 [3*30+10]
T = 2/11 [90+10]
T = 2/11 [100]
T = 200/11
T =18 2/11
The answer indicates that the hands of a clock will make an angle of 10 between 3 and 4 o’clock at exactly 3:18:2/11 ( 3’ o clock 18 minutes and 2/11 of minutes = 2/11*60 = 10.9 seconds)
Correct clock v/s Wrong clock
This section involves the comparison of time in the accurate clock with the wrong watch. The wrong time indicates that a clock is either slow or fast compared to the correct time. The wrong clock can either be fast or delayed by a few seconds/minutes/ hours or sometimes by a few days and weeks.
Example 3: A clock gains 5 seconds for every 3 minutes. If the clock started working at 7 a.m. in the morning, then what will be the time in the wrong clock at 4 p.m. on the same day?
Sol:
A clock gains 5 seconds for every 3 minutes, then it will gain 50 seconds in 30 minutes, or it will acquire 100 seconds in 60 minutes. i.e. it will gain 100 seconds in 1 hour. Since the clock was started at 7 a.m. in the morning and right now the correct time is 4 p.m. the total time the clock has worked is 9 hours. We know that in 1 hour it gains 100 seconds then in 9 hours it increases 900 seconds. The conversion of 900 seconds to minutes will be 15 minutes. This increase indicates that a clock is faster by 15 minutes as the clock is gaining. Hence, the time in the watch would be 4:15 p.m.
|
167 videos|238 docs|95 tests
|




















