Overview: Inequalities | Quantitative Aptitude (Quant) - CAT PDF Download
What is Inequality?
- Inequalities are mathematical expressions in which both sides are not equal.
- In inequality, unlike in equations, we compare two values.
- The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
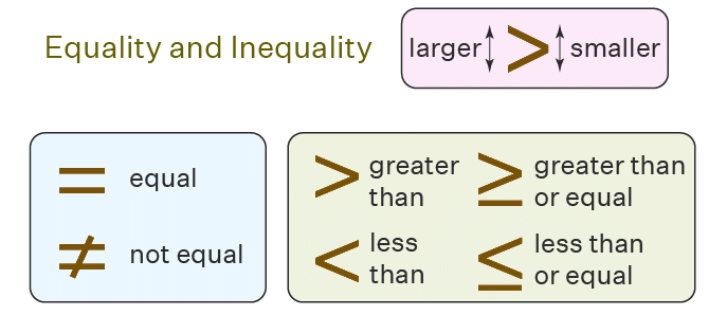
- The meaning of inequality is to say that two things are NOT equal. One of the things may be less than, greater than, less than or equal to, or greater than or equal to the other things.
- p ≠ q means that p is not equal to q
- p < q means that p is less than q
- p > q means that p is greater than q
- p ≤ q means that p is less than or equal to q
- p ≥ q means that p is greater than or equal to q
Properties of Inequalities
There is a certain set of properties that stand true for any symbol of inequality that is used in an expression. Sona of those properties are as follows;
1. Transitivity: this is the relation that is established in the hm three values.
If a ≥ b, and b ≥ c, then a ≥ c
2. Addition or subtraction property: If the same value is added to or subtracted from both sides of an inequality expression, the symbol of inequality will remain the same.
If a < b, then a + x < b + x
3. Multiplication or division property: If a positive quantity is used to multiply or divide the expression on both sides, then the symbol of inequality remains the same. If the value is negative, then the symbol changes.
If a < b, m < 0, then a × m > b × m
If a < b, m > 0, then a × m < b × m
Some Important Inequalities

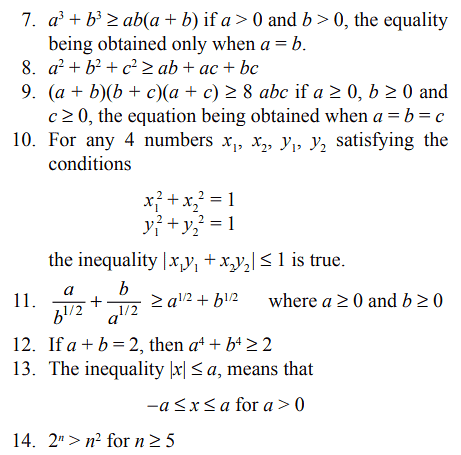
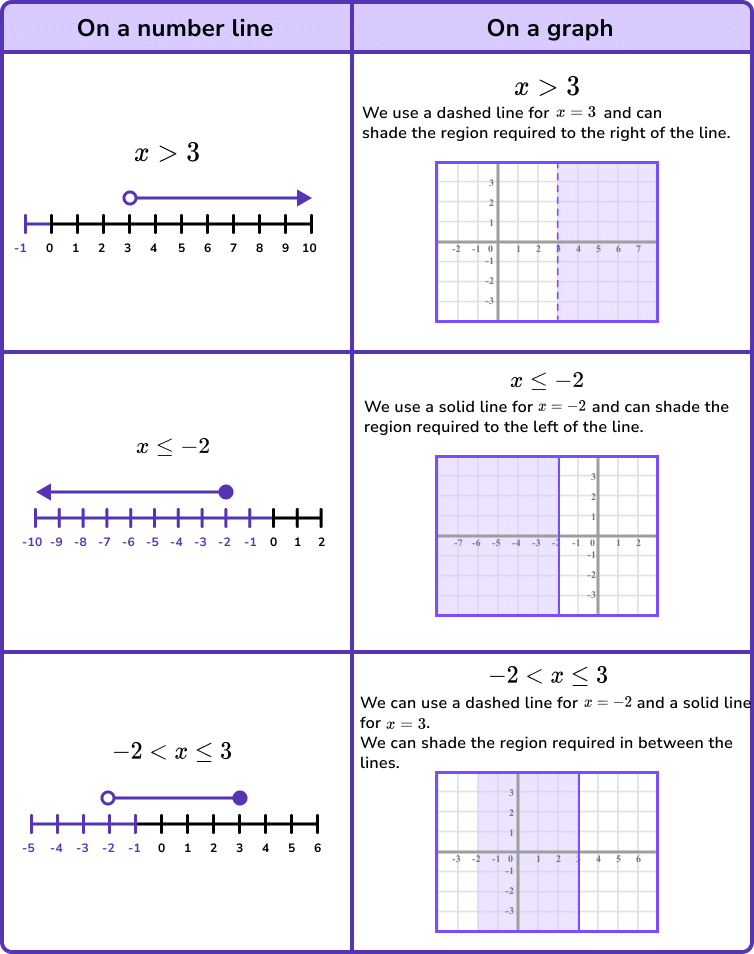
Graphing Inequalities
While graphing inequalities, we have to keep the following things in mind.
- If the endpoint is included (i.e., in case of ≤ or ≥) use a closed circle.
- If the endpoint is NOT included (i.e., in case of < or >), use an open circle. Use open circle at either ∞ or -∞.
- Draw a line from the endpoint that extends to the right side if the variable is greater than the number.
- Draw a line from the endpoint that extends to the left side if the variable is lesser than the number.
Writing Inequalities in Interval Notation
While writing the solution of an inequality in the interval notation, we have to keep the following things in mind.
- If the endpoint is included (i.e., in case of ≤ or ≥) use the closed brackets '[' or ']'
- If the endpoint is not included (i.e., in case of < or >), use the open brackets '(' or ')'
- Use always open bracket at either ∞ or -∞.
Solving Linear Inequalities in One Unknown
A linear inequality is defined as an inequality of the form  where the symbol ‘I’ represents any of the inequalities < , >, ≥ ,
where the symbol ‘I’ represents any of the inequalities < , >, ≥ , 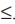 .
.
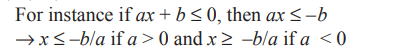
Example: Solve the inequality 2(x – 3) –1 > 3(x – 2)– 4(x + 1)
>>> 2x – 7 > 3x – 6 – 4x – 4
>>> 3x > –3.
Hence, x > –1
This can be represented in mathematical terms as (–1,+∞)
Solving Quadratic Inequalities
A quadratic inequality is defined as an inequality of the form:
ax2 + bx + c I 0 (a 0) where the symbol I represents any of the inequalities <, >, ≥,
0) where the symbol I represents any of the inequalities <, >, ≥, 
For a quadratic expression of the form ax2 + bx + c,
(b2– 4ac) is defined as the discriminant of the expression and is often denoted as D. i.e. D = b2– 4ac
The following cases are possible for the value of the quadratic expression: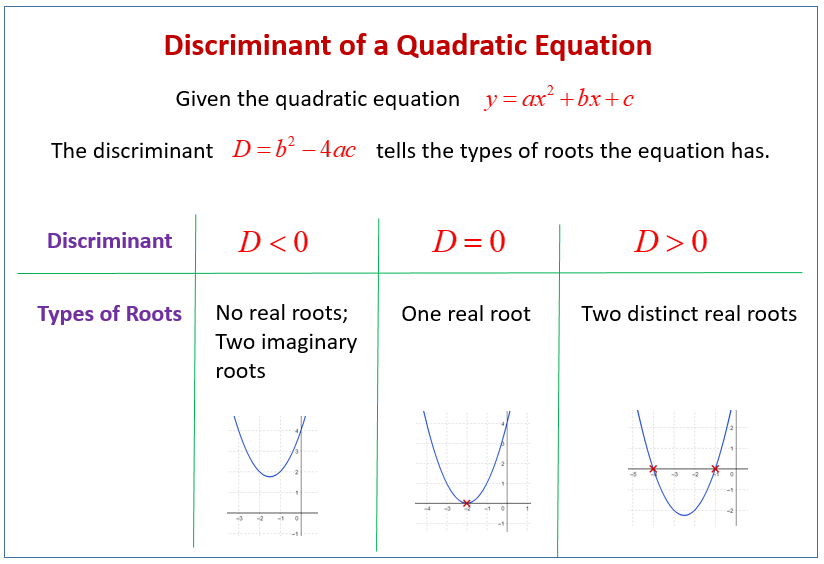
Case 1: If D < 0

In other words, we can say that if D is negative then the values of the quadratic expression takes the same sign as the coefficient of x2.
This can also be said as
If D < 0 then all real values of x are solutions of the inequalities ax2 + bx + c > 0 and ax2+ bx + c ≥ 0 for a > 0 and have no solution in case a < 0.
Also, for D < 0, all real values of x are solutions of the inequalities ax2+ bx + c < 0 and ax2 + bx + c  0 if a < 0 and these inequalities will not give any solution for a > 0.
0 if a < 0 and these inequalities will not give any solution for a > 0.
Case 2: D = 0
If the discriminant of a quadratic expression is equal to zero, then the value of the quadratic expression takes the same sign as that of the coefficient of x2 (except when x = –b/2a at which point the value of the quadratic expression becomes 0).
We can also say the following for D = 0:
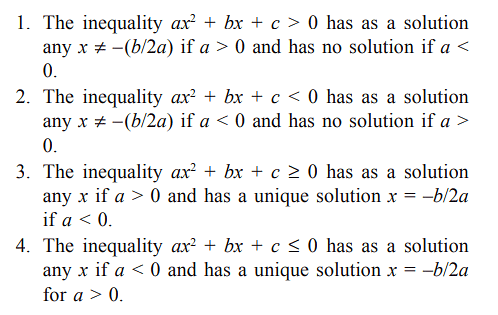
Case 3: D > 0
If x1 and x2 are the roots of the quadratic expression then it can be said that:
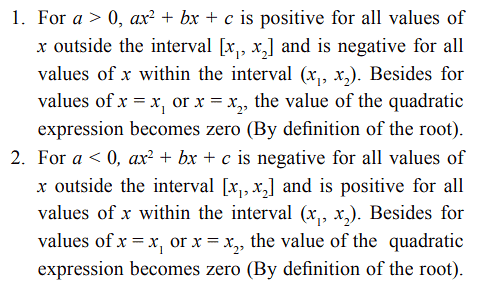
Example: x2 – 5x + 6 > 0
Solution: (a) The discriminant D = 25 – 4 x 6 > 0 and a is positive (+1); the roots of the quadratic expression are real and distinct: x1
= 2 and x2= 3. By the property of quadratic inequalities, we get that the expression is positive outside the interval [2, 3]. Hence, the solution is x < 2 and x > 3.
We can also see it as x2– 5x + 6 = (x – 2) (x – 3) and the given inequality takes the form (x – 2) (x – 3) > 0.
The solutions of the inequality are the numbers x < 2 (when both factors are negative and their product is positive) and also the numbers x > 3 (when both factors are positive and, hence, their product is also positive).
Answer: x < 2 and x > 3.
System of Inequalities in One Unknown
- Let there be given several inequalities in one unknown. If it is required to find the number that will be the solution of all the given equalities, then the set of these inequalities is called a system of inequalities. The solution of a system of inequalities in one unknown is defined as the value of the unknown for which all the inequalities of the system reduce to true numerical inequalities.
- To solve a system of inequalities means to find all the solutions of the system or to establish that there is none.
- Two systems of inequalities are said to be equivalent if any solution of one of them is a solution of the other, and vice versa. If both the systems of inequalities have no solution, then they are also regarded to be equivalent.
Example: Solve the system of inequalities:
3x – 4 < 8x + 6
2x – 1 > 5x – 4
11x – 9  15x + 3
15x + 3
Solution: We solve the first inequality:
3x – 4 < 8x + 6
–5x < 10
x > –2
It is fulfilled for x > –2.
Then we solve the second inequality
2x – 1 > 5x – 4
–3x > – 3
x < 1
It is fulfilled for x < 1.
And, finally, we solve the third inequality:
11x – 9 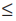 15x + 3
15x + 3
–4x 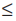 12
12
x ≥ – 3
It is fulfilled for x ≥ – 3. All the given inequalities are true for – 2 < x < 1.
Inequalities Containing a Modulus
| x | 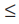 a, where a > 0 means the same as the double inequality
a, where a > 0 means the same as the double inequality
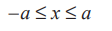
This result is used in solving inequalities containing a modulus.
Example: | 2x – 3 |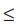 5
5
This is equivalent to –5 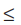 2x – 3
2x – 3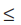 5
5
i.e. 2x – 3 ≥ –5 and 2x – 3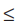 5
5
2x ≥ –2 x 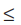 4
4
x ≥ –1
The solution is
–1 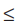 x
x 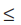 4.
4.
|
167 videos|229 docs|95 tests
|
FAQs on Overview: Inequalities - Quantitative Aptitude (Quant) - CAT
| 1. What is the significance of graphing inequalities in mathematics? |  |
| 2. How is writing inequalities in interval notation beneficial in solving mathematical problems? |  |
| 3. How can one effectively solve linear inequalities in one unknown? |  |
| 4. What is the approach to solving quadratic inequalities in mathematics? |  |
| 5. How are inequalities containing a modulus addressed in mathematical problems? |  |
















