Overview: Functions | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Domain and Range of a Function |

|
| Composition of functions |

|
| (i) Odd and Even Functions |

|
| (ii) Identical Functions |

|
| (iii) Greatest Integer Function |

|
Introduction
In mathematics, a function is a relation between a set of inputs (the domain) and a set of possible outputs (the codomain), such that each input is related to exactly one output. More formally, a function f from a set X to a set Y assigns to every element x in X exactly one element y in Y.
Let A and B be two non-empty subsets. A relation f from A to B i.e. a sub set of A x B is called a function from A to B, If
- For each, a ϵ A there exists b ϵ B such that (a, b) ϵ f.
- (a, b) ϵ f and (a, c) ϵ f => b = c.
And that was the mathematical definition of Function now let’s learn what it means. In simple terms, if we have two set supposedly, for example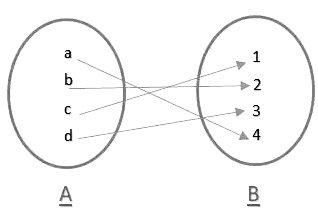 As given in above figure let there’s set A = {a, b, c, d} and set B = {1, 2, 3, 4} and let us call the set A be domain and B be codomain. Then, for each element present in A i.e. a, b, c, d there is a unique element corresponding to each of them in B. As you can see in the figure a goes to 4, b goes to 2, c goes to 1, and d goes to 3 i.e. for every element in domain there exist a unique element in codomain.
As given in above figure let there’s set A = {a, b, c, d} and set B = {1, 2, 3, 4} and let us call the set A be domain and B be codomain. Then, for each element present in A i.e. a, b, c, d there is a unique element corresponding to each of them in B. As you can see in the figure a goes to 4, b goes to 2, c goes to 1, and d goes to 3 i.e. for every element in domain there exist a unique element in codomain.
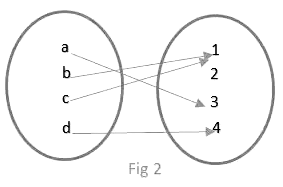
Now which of the above is a Function?
Fig 1 and Fig 3 are not functions (Why?). The answer lies in its definition. Therefore, Fig 1 is not a function reason being that in its Domain a has two images 2 and 4 which is not possible because as given in definition every element in its domain should have a unique image but here this is not the case. Similarly, Fig 2 is not a function with the same reason that here c in domain has got no image in codomain.
And, Fig 2 is a function as it satisfies the criteria of being a function that every element here in Fig 2 has got a unique image in its codomain.
Now that we have understood what conditions are necessary for functions. We can move to the basic properties and nature of functions.
Firstly, the basic notation of functions is Y = f(x)
Therefore, for any quadratic equation such as Y= x2+x+5 can be re-written as f(x)= x2+x+5 or g(x)= x2+x+5.
Now, what is f (2) in the above function?
We will just replace x from above function by 2 and we will get the values. f(2) = 22+ 2+ 5 =4+ 2+ 5 =11
Domain and Range of a Function
The set of all the inputs for a given function is called the domain of a function or if f: R→Z, here f is defined from real numbers to integer values. Then here the set of real numbers is a domain of a function. Here the set of integers Z is known as codomain. Similarly, all the set of outputs (dependent variable) we get by plugging into the set of all inputs ( domain) in a given function is known as range of a function.
Before moving on to questions that determine the domain and range of a function. Look at this table given below.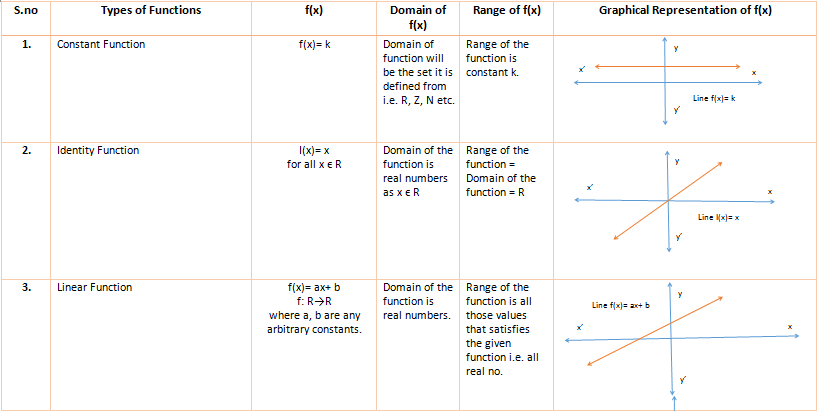


Now we are in a position to solve a few questions on domain and range of function. Let’s start with a basic example:
Example: Find range and domain of f(x)= x/ (x²+1).
Ans: Clearly, the domain of f(x)= R.
Let y= f(x). Then,
Y= f(x) => y= x/(x²+1)
x²y- x+ y= 0
x= (1±√1-4y²)/ 2y
Clearly, x will assume real values, if
1-4y²≥0 and y≠0 => 4y²-1≤0 and y≠0
⇒ y²-¼≤0 and y≠0
⇒ (y-½) (y+½) ≤0 and y≠0
⇒ -½≤y≤½and y≠0
⇒ y ϵ [-½, ½]- {0}
Example: Find the domain of f(x)= (√x-|x|)⁻¹
Ans: Since, |x|= {x, if x≥0
-x, if x<0}
⇒ x- |x|= {x-x= 0, if x≥0
x+ x= 2x, if x<0}
⇒ x- |x|≤0 for all x
⇒ 1/(√x-|x|) does not take any real values for any x ϵ R
⇒ f(x) is not defined for any x ϵ R
Hence, Domain (f)= φ.
Now that we have learned about domain and range of function we can move to another topic in function of importance which is Composition of Functions. But before directly hoping onto that we need to learn something about properties of functions given in following points.
- Injective Functions(Into Functions): A function is called injective (or one-to-one) if for any a, b ϵ domain such that a ≠ b then, f(a) ≠ f(b).
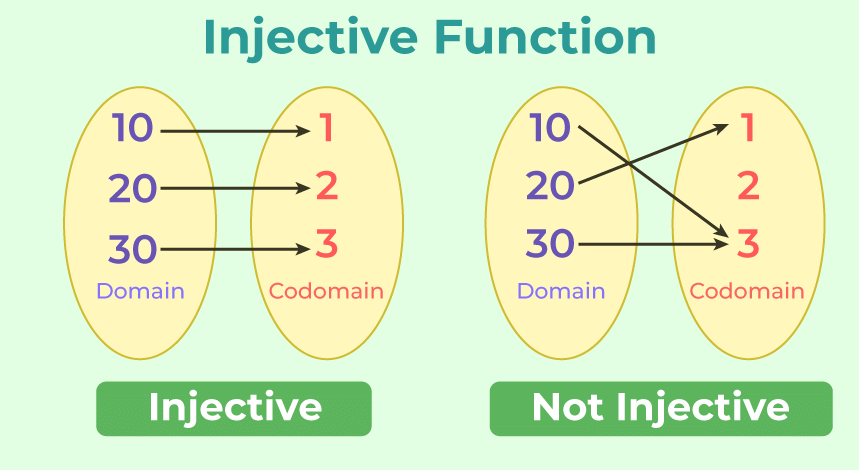
- Surjective Functions(Onto Functions) : A function is called surjective (or onto) if Range of the function = Codomain of the function.
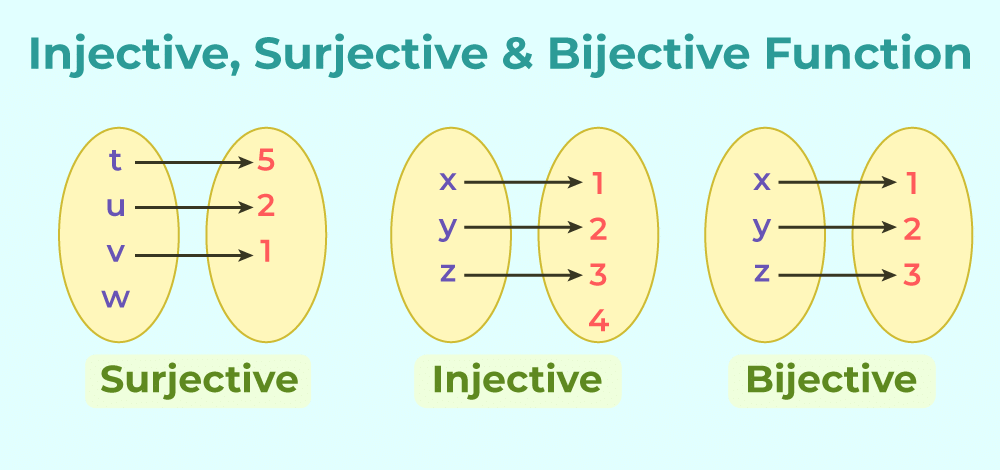
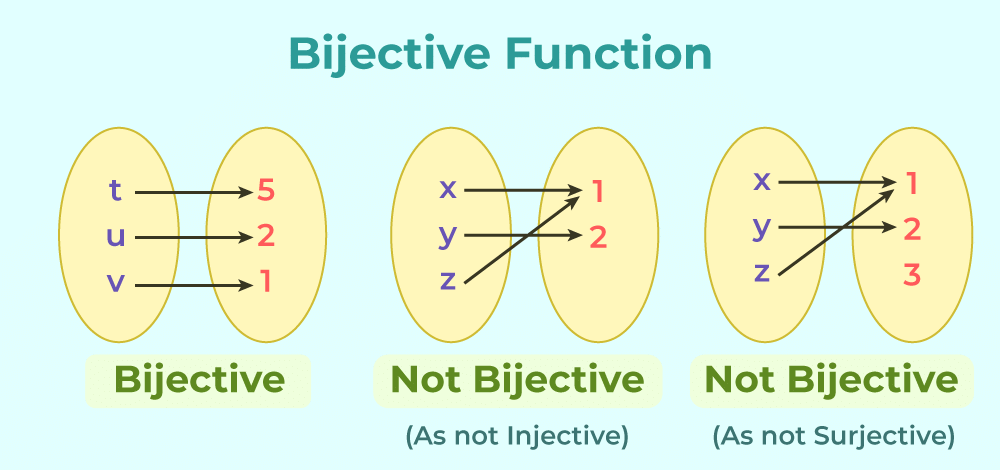
- Bijective Functions: A function is called bijective if it is both one-to-one and onto and is, therefore, invertible or the function has an inverse.
Composition of functions
Suppose we have two functions f(x) and g(x), such that f: R→ R and G: R→ R the ꓱ a function fog(x) such that fog: R→ R or a function gof(x) such that gof: R→ R known as composition of function. In simple terms if output of one function becomes input of another it is known as composition.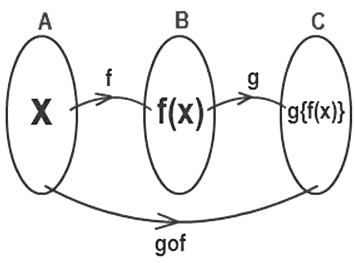
Condition Necessary for composition of functions
- fog(x) exists, if Range of f = Domain of g.
- Similarly, gof(x) exists, if range of g= Domain of f.
- If fog(x) = gof(x) = x then g is inverse of f and vice versa.
Let’s do one example now to understand the use of this concept.
Example: If f(x)= 2x+5 and g(x)= x² then what is gof(x) and fog(x)?
Ans: gof(x)= g(f(x))= g(2x+5)= (2x+5)²= 4x²+20x+25.
Similarly, fog(x)= f(g(x))= f(x²)= 2x²+5.
You can solve any question on composition on similar lines as given above.
(i) Odd and Even Functions
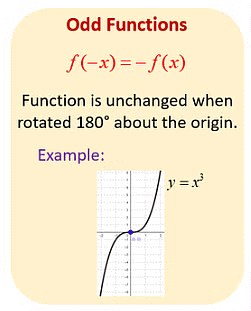
- Odd Function: A function is said to be odd if, f(-x)= -f(x) i.e. the graph of odd function is symmetric about origin. Examples of odd functions are x⁻¹, sin(x) etc.
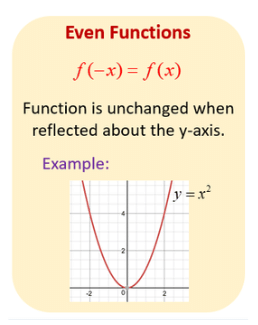
- Even Functions: A function is called even function if, f(-x) = f(x) i.e. the graph of even is symmetric about the y-axis. Examples of even functions are x², cos(x) etc.
- Neither odd nor even Functions: There is a third category of functions called neither odd nor even that exists if the graph of function does not exhibit symmetry. Example of such type are f(x)= 2x.
Note: f(x)= 0 is both odd and even function.
Example: If f(x) is a polynomial of degree 8 and f(x)f(1/x) = f(x) + f (1/x), then f(x) is odd, even or neither odd or even function?
Ans: Let f(x)= a₀x⁸ + a₁x⁷+….+a₇x + a₈
⇒ f(1/x)= a₀/x⁸ + a₁/x⁷+….+a₇/x + a₈
Now f(x)f(1/x) = f(x) + f(1/x)
⇒ (a₀x⁸ + a₁x⁷+….+a₇x + a₈) (a₀/x⁸ + a₁/x⁷+….+a₇/x + a₈)= (a₀x⁸ + a₁x⁷+….+a₇x + a₈) +( a₀/x⁸ + a₁/x⁷+….+a₇/x + a₈)
Comparing the coefficients of like powers on both the sides, we get
a₀ = ±1, a₈=1, a₁ = a₂ =… = a₇ = 0
Therefore, f(x)= ±x⁸ + 1
⇒ f(-x) = ±x⁸ + 1
Hence, it is an even function.
Example: If f(x − 1) + f(x + 1) = f(x) and f(2) = 6, f(0) = 1, then what is the value of f(50)?
1) −7
2) 6
3) 1
4) 7
Ans: Since we know both f(0)=1 and f(2)=6, we can find f(1).
By plugging the value of x=1f(1) = f(0) + f(2) = 7
f(2) = f(1) + f(3)
f(3) = f(2) – f(1)
= 6 – 7
= −1
Also, f(3) = f(2) + f(4)
f(4) = f(3) – f(2) = −7
Continuing in a similar way, we can find out
f(0) = 1
f(1) = 7
f(2) = 6
f(3) = −1
f(4) = −7
f(5) = −6
f(6) = 1
f(7) = 7 and so on
After every 6 integral values of x, f(x) repeats itself.
f(6) = f(12) = f(18 ) = f(24) = f(30) = f(36) = f(42) = f(48 ) = 1
f(49) = 7
f(50) = 6
Example: If f(x) = 4x / (4x + 2)
Then find the value of f(1/100)+f(2/100)+ …+ f(99/100).
Ans : In these type of questions , an important observation has to be made regarding the pattern involved in the “required part”
(1/100 +99/100) = 1 and 99/100 = (1 -1/100) so f(x) and f(1-x) has a certain relation.
f (x) = 4x/4x + 2………(1)
f (1 – x) = 4(1 – x) / 4(1 – x) + 2. ……..(2)
= 4/4 + 2.4x
= 2/2 + 4x.
On adding both the equations (1)and (2), we get
f(x) + f(1 – x) = [4x/4x + 2] + [2/4x + 2 ]= 1.
Hence a generalisation is obtained,
f(1 / 100) + f(1 – 1/100) = f(1) + f(99/100) = 1.
f (2/100) + f( 1 – 2/100) = f(2) + f(98/100) = 1.
Similarly f(49/100) + f(50/100) = 1.
Hence f(1/100) + f(2/100) + f(3/100)………………………..f(99/100)
= 49.
(ii) Identical Functions
In mathematics, two functions are said to be identical if they have the same domain, the same codomain, and assign the same output to every input in their common domain.
Formally, let's say we have two functions f and g. We denote them as f(x) and g(x). These functions are identical if:
- They have the same domain, meaning they accept the same inputs.
- They have the same codomain, meaning they produce outputs from the same set.
- For every input value x in their common domain, f(x) = g(x).
Example: Check whether two functions f(x)= root(x2) and g(x) = |x| are identical or not.
Ans: In f(x) for every real value of x , there is a value of f(x), which means x belongs to R
In G(x) for every real value of x, there is a value of g(x), which also means x belongs to R.
In both the cases, the domain is same. Hence, The Functions are “IDENTICAL”
Example 2: Now again we have two functions f(x)= ln (x2 -5x +6) and g(x)= ln(x-2) + ln(x-3) are identical or not.
Ans: The ln values cannot be negative or zero . So we will analyse both cases.
x2 -5x +6x >0 ⇒ (x-2)(x-3)>0 ⇒ x belongs (-infinity,2)U(3,infinity)=> (x-2)>0 and (x-3)>0 ⇒ x>2 and x>3 ⇒ x belongs to (2, infinity)
In both cases there are different domains ,so the functions are “NOT IDENTICAL”.
(iii) Greatest Integer Function
The greatest integer function, often denoted as ⌊x⌋ or sometimes as "floor" function, is a mathematical function that gives the greatest integer less than or equal to a given real number. In other words, it rounds down to the nearest integer.

Greatest Integer Function, [x] indicated the integral part of x is nearest and smallest integer to x. It is also known as floor of x.
e.g. [9.638] = 9, [7] = 7, [0.286] = 0, [-3.432] = -4, [-0.432] = -1
In general, n = x < n+1 , where n is an integer, [x] = n
Now, we can say that for any real number x, x = I + f
where,
I = Integral Part denoted by [x]
f = Fractional Part denoted by {x}
Thus, {x} = x – [x]
Example: Find the value of [3/4] + [3/4 + 1/100] + [3/4+ 2/100] +……..+ [3/4 + 99/100].
Ans: [3/4] + [3/4+ 1/100] + [3/4+ 2/100] +… [3/4+25/100]+[3/4+26/100]+ ? + [3/4+ 99/100]
First of all the number of terms in the series is 100.
[3/4]=[0.75]=0
[3/4 + 1/100]= [0.75 + 0.01]=[0.76]=0
similarly the frist 25 terms will be equal to 0 (as 25th term is [3/4 + 25/100]=[3/4 +1/4]=1)
and from the 26th term each term will be equal to 1.
First 25 terms are 0 and the next 75 terms are 1.
So, sum of all the terms = (25 × 0) + (75 × 1) = 75
|
167 videos|238 docs|95 tests
|
FAQs on Overview: Functions - Quantitative Aptitude (Quant) - CAT
| 1. What is the domain and range of a function? |  |
| 2. How do you find the composition of functions? |  |
| 3. What are odd functions and even functions? |  |
| 4. How can you determine if a function is odd, even, or neither? |  |
| 5. Can a function be both odd and even at the same time? |  |















