| Table of contents |

|
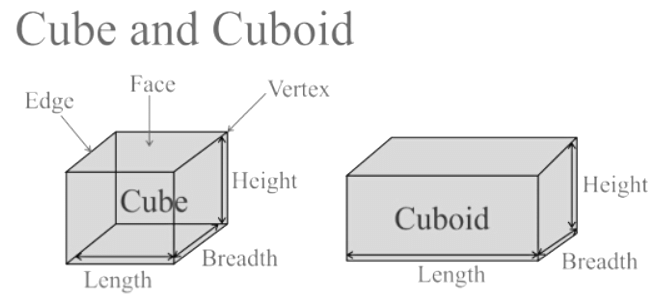
| Cube and Cuboid |

|
| Net of a Cube |

|
| Formulas of a Cube |

|
| Total Surface of a Cube |

|
| Volume of a Cube |

|
| Cuboid |

|
| Net of a Cuboid |

|
| Formulas of a Cuboid |

|
| Solved Examples – Cube and Cuboid Formula |

|
Cube and Cuboid
In our daily life, we see many objects like notebooks, matchboxes, instrumental geometry boxes, cones, cricket balls, cylinders, etc. These are all three-dimensional objects (solid shapes). All these objects occupy some shape and have three dimensions Length, Breadth, Height, or Depth.
Moreover, we often find some shapes with two or more identical (congruent) faces. For example, the Cube has squared faces on each side, and the Cuboid has rectangular faces on each side. A Cube and Cuboid is a three-dimensional shape with six faces, eight vertices, and twelve edges. The main distinction is that a cube has the same length, width, and height on all sides, whereas a cuboid has varied length, breadth, and height. Both shapes appear to be nearly the same, however, they have different properties.
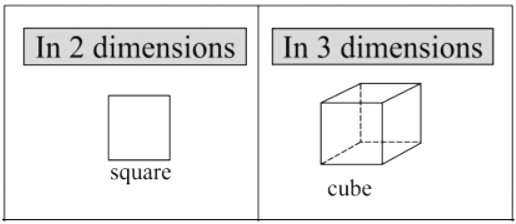
A square is a two-dimensional figure with two dimensions length and breadth, while a cube is a three-dimensional figure with three dimensions length, breadth, and height. The side faces of a cube are formed by squares. Also knowing the cube and cuboid formula will enable students to know the difference between cube and cuboid easily.
Common examples of Cube in real life are square ice cubes, dice, sugar cubes, Rubik’s cube etc.
A cube shape is like that of perfect square. Cube is a three-dimensional box-like figure represented in the three-dimensional plane. Cube has 6 square-shaped equal faces. Each face meets another face at 90o each. Three sides of the cube meet at the same vertex.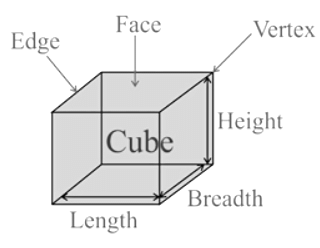
In the given figure, faces, edges and vertices of a cube have been shown. 8 corners of the cube are its vertices. The line segments forming the cube are its 12 edges. The six square faces forming the cube are its 6 faces.
- Faces of a Cube: Polygon regions forming a solid are called its faces.
- Edges of a Cube: Line segments where the faces meet are called its edges.
- Vertices of a Cube: Points of intersection of three faces of a solid are called its vertices.
Net of a Cube
The net of a solid is a diagram drawn on paper which when cut and folded along the lines can be used to construct a solid shape. Net of a Cube is a two-dimensional shape that can be folded into a three dimensional figure is a Cube.
A Cube consists of 6 square faces, 12 edges, and 8 vertices. When the square faces of a cube are separated at the edges and laid out flat, they make a two-dimensional figure called a net.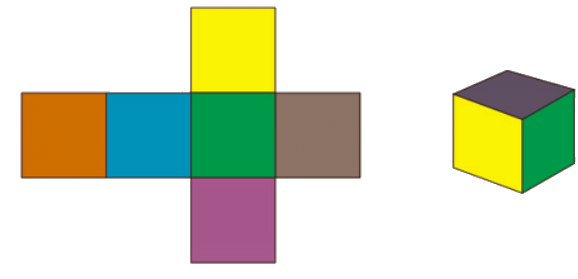
Formulas of a Cube
Lateral Surface Area of a Cube:
Consider a Cube of edge length ‘a′ , then, the area of each face of a square = a2
So, the Lateral Surface Area of a Cube = Sum of the area of all 4 side faces Lateral Surface Area(LSA) = 4a2 square units
Total Surface of a Cube
We know the cube consists of 6 square faces. Let us consider if each side of a cube is a , then the total surface area of the Cube is = 6a2.
Total Surface Area (TSA) = 6a2 square units
Volume of a Cube
The volume of a cube can be found by multiplying the edge length three times. If each edge length is “a” , then the Volume of a Cube is a3.
V = a3 cubic units
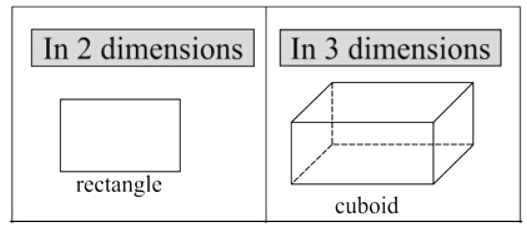
Cuboid
A rectangle is a two-dimensional figure with two dimensions length and breadth, while a cuboid is a three-dimensional figure with three dimensions length, breadth, and height. The side faces of a cuboid are formed by rectangles.
 Common examples of cuboid in real life are bricks, the lunch box, notebook, and Geometry instrumental box.
Common examples of cuboid in real life are bricks, the lunch box, notebook, and Geometry instrumental box. Cuboid is a three-dimensional box-like figure represented in the three-dimensional plane. Cuboid has 6 rectangular-shaped equal faces. Each face meets another face at 90o each. Three sides of the cuboid meet at the same vertex.
Cuboid is a three-dimensional box-like figure represented in the three-dimensional plane. Cuboid has 6 rectangular-shaped equal faces. Each face meets another face at 90o each. Three sides of the cuboid meet at the same vertex.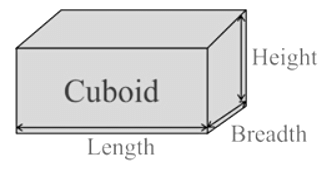
Net of a Cuboid
A cuboid consists of 6 rectangular faces, 12 edges, and 8 vertices. When the rectangular faces of a cuboid are separated at the edges and laid out flat, they make a two-dimensional figure called a net of a Cuboid. A cuboid shape is like that of a rectangular shoe box.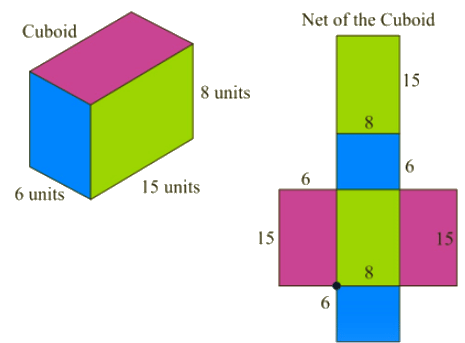
Formulas of a Cuboid
Lateral Surface Area of a Cuboid
- Lateral Surface Area of a cuboid = Sum of four vertical sides
- Lateral Surface Area (LSA) = 2h(l + b) square units
Total Surface of a Cuboid
We know the cuboid consists of 6 rectangular faces.
Total Surface Area (TSA) =2(lb+bh+hl) square units
Where, l= length, b= breadth, h= height
Volume of a Cuboid
Volume of a cuboid is V = length × breadth × height
V = (l × b × h) Cubic units
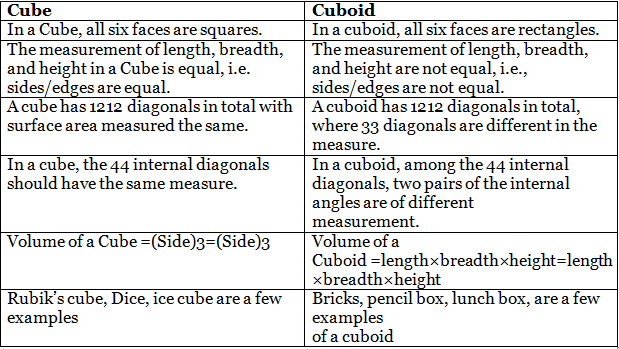
Difference Between Cube and Cuboid
Solved Examples – Cube and Cuboid Formula
Q1: Find the volume of the cube whose each edge is 5cm.
Ans: From the given edge a = 5cm
Volume of a Cube is a3.
V = a3 cubic units
⇒ V = 53
⇒ V = 125cm3
Hence, the volume of a Cube is 125cm3.
Q2: Find the volume of the cuboid whose dimensions are length = 6m , breadth = 6m , height = 6m.
Ans: Given: = 6m,breadth = 4m, height = 3m
Volume of a Cuboid =length × breadth × height
⇒ Volume of a Cuboid = 6 × 4 × 3
⇒ V = 72m3
Hence, the volume of a Cuboid is 72m3.
Q3: Find the surface area of a cube whose edge is 6cm.
Ans: From the given = 6cm
The total surface area of the Cube is 6a2.
Total Surface Area (TSA)=6×(6)2 square units
= 6 × 36 = 216cm2
Hence, the surface area of a Cube is 216cm2.
Q4: What is the lateral surface area of a cube of edge 10cm
Ans: From the given = 10cm
The Lateral Surface Area of a Cube = Sum of area of all 4 side faces
Lateral Surface Area(LSA) =4a2 square units
⇒ LSA = 4 × 102
⇒ LSA = 4 × 100
⇒ LSA = 400cm2
Hence, the obtained lateral surface area of a cube is 400cm2.
Q5: A cuboid-shaped wooden block has 5cm length, 4cm breadth and 5cm height. Find the total surface area of a Cuboid.
Ans: Given: Length 5cm , Breadth 4cm , Height 5cm
Total Surface Area (TSA) = 2(lb+bh+hl) square units
⇒ TSA = 2(5×4+4×1+1×5)
⇒ TSA = 2(20+4+5)
⇒ TSA = 2(29)
⇒ TSA = 58cm2
Hence, the obtained total surface area of a Cuboid is 58cm2.
FAQs on Overview: Cubes & Cuboids - CAT
| 1. What is the net of a cube? |  |
| 2. What are the formulas for a cube? |  |
| 3. What is the net of a cuboid? |  |
| 4. What are the formulas for a cuboid? |  |
| 5. Can you provide an example of how to use the cube and cuboid formulas? |  |














