NCERT Solutions Class 11 Maths Chapter 7 - Binomial Theorem

Question 1: If a and b are distinct integers, prove that a – b is a factor of aⁿ – bⁿ, whenever n is a positive integer.

[Hint: write aⁿ = (a – b  + b)ⁿ and expand]

ANSWER : - In order to prove that (a – b) is a factor of (aⁿ – bⁿ), it has to be proved that

aⁿ – bⁿ = k (a – b), where k is some natural number

It can be written that, a = a – b +  b

This shows that (a – b) is a factor of (aⁿ – bⁿ), where n is a positive integer.

Question 2: Evaluate .

ANSWER : - Firstly, the expression (a  + b)⁶ – (a – b)⁶ is simplified by using Binomial Theorem.

This can be done as

Question 3: Find the value of .

ANSWER : - Firstly, the expression (x  + y)⁴  (x – y)⁴ is simplified by using Binomial Theorem.

This can be done as

 Question 4: Find an approximation of (0.99)⁵ using the first three terms of its expansion.

ANSWER : - 0.99 = 1 – 0.01

Thus, the value of (0.99)⁵ is approximately 0.951.

Question 5: Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of 

ANSWER : - In the expansion,  ,

Fifth term from the beginning

Fifth term from the end

Therefore, it is evident that in the expansion of , the fifth term from the beginning is  and the fifth term from the end is .

It is given that the ratio of the fifth term from the beginning to the fifth term from the end is . Therefore, from (1) and (2), we obtain

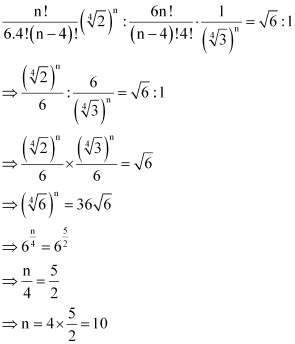
Thus, the value of n is 10.

Question 6: Expand using Binomial Theorem .

 ANSWER : - Using Binomial Theorem, the given expression   can be expanded as

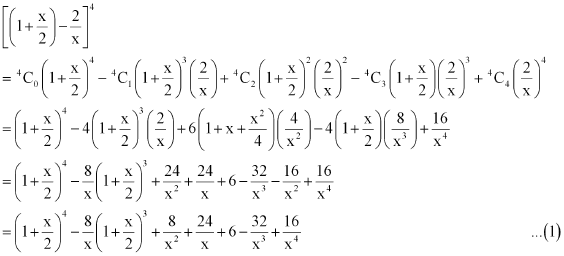
Again by using Binomial Theorem, we obtain

From (1), (2), and (3), we obtain

Question 7: Find the expansion of  using binomial theorem.

 ANSWER : - Using Binomial Theorem, the given expression   can be expanded as

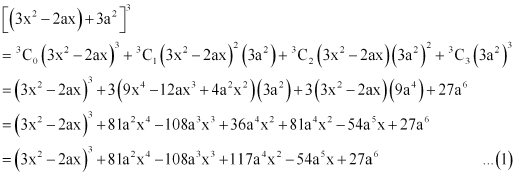
Again by using Binomial Theorem, we obtain

From (1) and (2), we obtain