JEE Exam > JEE Notes > Mathematics (Maths) Class 12 > NCERT Solutions - Exercise Miscellaneous : Application of Integral
NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
Question 1: Find the area under the given curves and given lines:
(i) y = x2, x = 1, x = 2 and x-axis
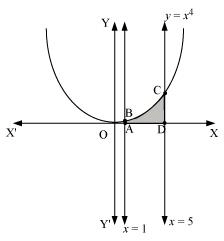
(ii) y = x4, x = 1, x = 5 and x –axis
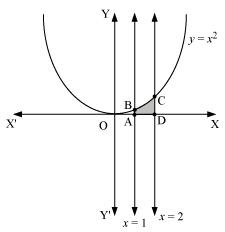
ANSWER : - (i) The required area is represented by the shaded area ADCBA as
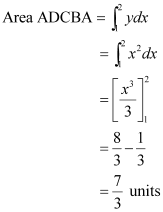
- The required area is represented by the shaded area ADCBA as
Question 2: Sketch the graph of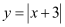 
and evaluate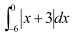
ANSWER : -The given equation is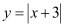 
The corresponding values of x and y are given in the following table.
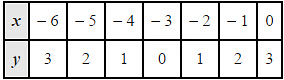
On plotting these points, we obtain the graph of 
as follows.
It is known that,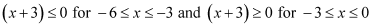 
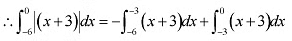
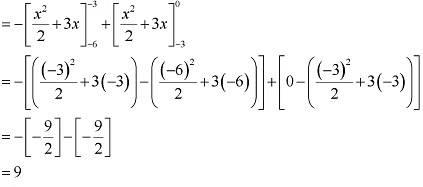
Question 3: Find the area bounded by the curve y = sin x between x = 0 and x = 2π
ANSWER : -The graph of y = sin x can be drawn as
∴ Required area = Area OABO Area BCDB
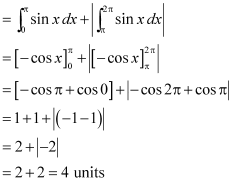
Question 4: Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is
A. – 9
B.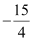 
C.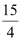 
D.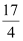 
ANSWER : -
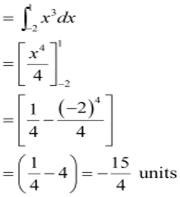
Thus, the correct answer is B.
Question 5:The area bounded by the curve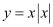
, x-axis and the ordinates x = –1 & x = 1 is given by [Hint: y = x2 if x > 0 and y = –x2 if x < 0]
A. 0
B.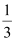 
C.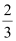 
D.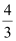 
ANSWER : -
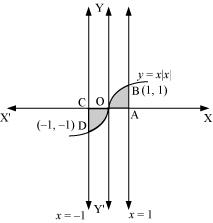
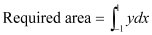
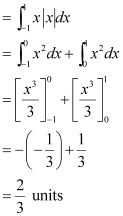
Thus, the correct answer is C.
The document NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral is a part of the JEE Course Mathematics (Maths) Class 12.
All you need of JEE at this link: JEE
|
204 videos|290 docs|139 tests
|
FAQs on NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
| 1. What are the different applications of integrals? |  |
Ans. Integrals have various applications in real-life scenarios. Some common applications include finding areas and volumes, calculating work done, determining the center of mass, analyzing population growth, and solving differential equations.
| 2. How can integrals be used to find areas and volumes? | |
Ans. Integrals can be used to find the area under a curve, which represents the area between the curve and the x-axis. Similarly, integrals can also be used to find the volume of a solid obtained by rotating a curve around an axis, using the method of disks or washers.
| 3. What is the significance of integrals in calculating work done? | |
Ans. Integrals are used to calculate work done in physics. By integrating a force function over a given displacement, the integral gives the work done by the force. This is particularly useful in situations where the force varies along the path.
| 4. How can integrals be applied to determine the center of mass? | |
Ans. Integrals are used to calculate the center of mass of an object. By considering the mass distribution and integrating over the object's volume or area, the integral gives the coordinates of the center of mass.
| 5. Can integrals be used to solve differential equations? | |
Ans. Yes, integrals play a crucial role in solving differential equations. By integrating both sides of a differential equation, it is possible to obtain a general solution. Integrating further with appropriate initial or boundary conditions can yield specific solutions.
Related Exams
About this Document
|
Nov 22, 2024 Last updated |
Document Description: NCERT Solutions - Exercise Miscellaneous : Application of Integral for JEE 2024 is part of Mathematics (Maths) Class 12 preparation.
The notes and questions for NCERT Solutions - Exercise Miscellaneous : Application of Integral have been prepared according to the JEE exam syllabus. Information about NCERT Solutions - Exercise Miscellaneous : Application of Integral covers topics
like and NCERT Solutions - Exercise Miscellaneous : Application of Integral Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions - Exercise Miscellaneous : Application of Integral.
Introduction of NCERT Solutions - Exercise Miscellaneous : Application of Integral in English is available as part of our Mathematics (Maths) Class 12
for JEE & NCERT Solutions - Exercise Miscellaneous : Application of Integral in Hindi for Mathematics (Maths) Class 12 course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
Description
Full syllabus notes, lecture & questions for NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral - JEE | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 12 | Best notes, free PDF download
Information about NCERT Solutions - Exercise Miscellaneous : Application of Integral
In this doc you can find the meaning of NCERT Solutions - Exercise Miscellaneous : Application of Integral defined & explained in the simplest way possible. Besides explaining types of
NCERT Solutions - Exercise Miscellaneous : Application of Integral theory, EduRev gives you an ample number of questions to practice NCERT Solutions - Exercise Miscellaneous : Application of Integral tests, examples and also practice JEE
tests
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
practice quizzes
,video lectures
,mock tests for examination
,past year papers
,Free
,Previous Year Questions with Solutions
,Objective type Questions
,NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
,NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
,shortcuts and tricks
,Summary
,Viva Questions
,Semester Notes
,Exam
,NCERT Solutions Class 12 Maths Chapter 8 - Application of Integral
,study material
,Important questions
,Sample Paper
,Extra Questions
,ppt
,MCQs
;
Additional Information about NCERT Solutions - Exercise Miscellaneous : Application of Integral for JEE Preparation
NCERT Solutions - Exercise Miscellaneous : Application of Integral Free PDF Download
The NCERT Solutions - Exercise Miscellaneous : Application of Integral is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the NCERT Solutions - Exercise Miscellaneous : Application of Integral now and kickstart your journey towards success in the JEE exam.
Importance of NCERT Solutions - Exercise Miscellaneous : Application of Integral
The importance of NCERT Solutions - Exercise Miscellaneous : Application of Integral cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
NCERT Solutions - Exercise Miscellaneous : Application of Integral Notes
NCERT Solutions - Exercise Miscellaneous : Application of Integral Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to NCERT Solutions - Exercise Miscellaneous : Application of Integral.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions - Exercise Miscellaneous : Application of Integral Notes on EduRev are your ultimate resource for success.
NCERT Solutions - Exercise Miscellaneous : Application of Integral JEE Questions
The "NCERT Solutions - Exercise Miscellaneous : Application of Integral JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study NCERT Solutions - Exercise Miscellaneous : Application of Integral on the App
Students of JEE can study NCERT Solutions - Exercise Miscellaneous : Application of Integral alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the NCERT Solutions - Exercise Miscellaneous : Application of Integral,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of NCERT Solutions - Exercise Miscellaneous : Application of Integral is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup