Q1: For each of the differential equations given below, indicate its order and degree (if defined).
(i) 
(ii) 
(iii) 
Ans: (i) The differential equation is given as:

The highest order derivative present in the differential equation is . Thus, its order is two. The highest power raised to
. Thus, its order is two. The highest power raised to  is one. Hence, its degree is one.
is one. Hence, its degree is one.
(ii) The differential equation is given as:

The highest order derivative present in the differential equation is . Thus, its order is one. The highest power raised to
. Thus, its order is one. The highest power raised to  is three. Hence, its degree is three.
is three. Hence, its degree is three.
(iii) The differential equation is given as:

The highest order derivative present in the differential equation is . Thus, its order is four.
. Thus, its order is four.
However, the given differential equation is not a polynomial equation. Hence, its degree is not defined.
Q2: For each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) 
(ii) 
(iii) 
(iv) 
Ans: (i) 
Differentiating both sides with respect to x, we get:

Again, differentiating both sides with respect to x, we get:

Now, on substituting the values of  and
and  in the differential equation, we get:
in the differential equation, we get:

⇒ L.H.S. ≠ R.H.S.
Hence, the given function is not a solution of the corresponding differential equation.
(ii) 
Differentiating both sides with respect to x, we get:

Again, differentiating both sides with respect to x, we get:

Now, on substituting the values of  and
and  in the L.H.S. of the given differential equation, we get:
in the L.H.S. of the given differential equation, we get:

Hence, the given function is a solution of the corresponding differential equation.
(iii) 
Differentiating both sides with respect to x, we get:

Again, differentiating both sides with respect to x, we get:

Substituting the value of  in the L.H.S. of the given differential equation, we get:
in the L.H.S. of the given differential equation, we get:

Hence, the given function is a solution of the corresponding differential equation.
(iv) 
Differentiating both sides with respect to x, we get:

Substituting the value of  in the L.H.S. of the given differential equation, we get:
in the L.H.S. of the given differential equation, we get:

Hence, the given function is a solution of the corresponding differential equation.
Q3: Form the differential equation representing the family of curves given by  where a is an arbitrary constant.
where a is an arbitrary constant.
Ans:

Differentiating with respect to x, we get:

From equation (1), we get:

On substituting this value in equation (3), we get:

Hence, the differential equation of the family of curves is given as 
Q4: Prove that  is the general solution of differential equation
is the general solution of differential equation , where c is a parameter.
, where c is a parameter.
Ans:

This is a homogeneous equation. To simplify it, we need to make the substitution as:

Substituting the values of y and  in equation (1), we get:
in equation (1), we get:

Integrating both sides, we get:


Substituting the values of I1 and I2 in equation (3), we get:

Therefore, equation (2) becomes:

Hence, the given result is proved.
Q5: Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
Ans: The equation of a circle in the first quadrant with centre (a, a) and radius (a) which touches the coordinate axes is:

Differentiating equation (1) with respect to x, we get:

Substituting the value of a in equation (1), we get:

Hence, the required differential equation of the family of circles is 
Q6: Find the general solution of the differential equation 
Ans:

Integrating both sides, we get:

Q7: Show that the general solution of the differential equation  is given by (x y 1) = A (1 – x – y – 2xy), where A is parameter
is given by (x y 1) = A (1 – x – y – 2xy), where A is parameter
Ans:

Integrating both sides, we get:



Hence, the given result is proved.
Q8: Find the equation of the curve passing through the point  whose differential equation is,
whose differential equation is, 
Ans: The differential equation of the given curve is:

Integrating both sides, we get:

The curve passes through point 

On substituting  in equation (1), we get:
in equation (1), we get:

Hence, the required equation of the curve is 
Q9: Find the particular solution of the differential equation  , given that y = 1 when x = 0
, given that y = 1 when x = 0
Ans:

Integrating both sides, we get:

Substituting these values in equation (1), we get:

Now, y = 1 at x = 0.
Therefore, equation (2) becomes:

Substituting  in equation (2), we get:
in equation (2), we get:

This is the required particular solution of the given differential equation.
Q10: Solve the differential equation 
Ans:

Differentiating it with respect to y, we get:

From equation (1) and equation (2), we get:

Integrating both sides, we get:

Q11: Find a particular solution of the differential equation , given that y = – 1, when x = 0 (Hint: put x – y = t)
, given that y = – 1, when x = 0 (Hint: put x – y = t)
Ans:

Substituting the values of x – y and  in equation (1), we get:
in equation (1), we get:

Integrating both sides, we get:

Now, y = –1 at x = 0.
Therefore, equation (3) becomes:
log 1 = 0 – 1 C
⇒ C = 1
Substituting C = 1 in equation (3) we get:

This is the required particular solution of the given differential equation.
Q12: Solve the differential equation 
Ans:

This equation is a linear differential equation of the form

The general solution of the given differential equation is given by,

Q13: Find a particular solution of the differential equation  , given that y = 0 when
, given that y = 0 when 
Ans: The given differential equation is:

This equation is a linear differential equation of the form

The general solution of the given differential equation is given by,

Now,
Therefore, equation (1) becomes:

Substituting  in equation (1), we get:
in equation (1), we get:

This is the required particular solution of the given differential equation.
Q14: Find a particular solution of the differential equation , given that y = 0 when x = 0
, given that y = 0 when x = 0
Ans:

Integrating both sides, we get:

Substituting this value in equation (1), we get:

Now, at x = 0 and y = 0, equation (2) becomes:

Substituting C = 1 in equation (2), we get:

This is the required particular solution of the given differential equation.
Q15: The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009
Ans: Let the population at any instant (t) be y.
It is given that the rate of increase of population is proportional to the number of inhabitants at any instant.

Integrating both sides, we get:
log y = kt + C … (1)
In the year 1999, t = 0 and y = 20000.
Therefore, we get:
log 20000 = C … (2)
In the year 2004, t = 5 and y = 25000.
Therefore, we get:

In the year 2009, t = 10 years.
Now, on substituting the values of t, k, and C in equation (1), we get:

Hence, the population of the village in 2009 will be 31250.
Q16: The general solution of the differential equation  is
is
A. xy = C
B. x = Cy2
C. y = Cx
D. y = Cx2
Ans: The given differential equation is:

Integrating both sides, we get:

Hence, the correct answer is C.
Q17: The general solution of a differential equation of the type  is
is
A. 
B. 
C. 
D. 
Ans: The integrating factor of the given differential equation
The general solution of the differential equation is given by,

Hence, the correct answer is C.
Q18: The general solution of the differential equation  is
is
A. xey + x2 = C
B. xey + y2 = C
C. yex + x2 = C
D. yey + x2 = C
Ans: The given differential equation is:

This is a linear differential equation of the form

The general solution of the given differential equation is given by,

Hence, the correct answer is C.




 . Thus, its order is two. The highest power raised to
. Thus, its order is two. The highest power raised to  is one. Hence, its degree is one.
is one. Hence, its degree is one.
 . Thus, its order is one. The highest power raised to
. Thus, its order is one. The highest power raised to  is three. Hence, its degree is three.
is three. Hence, its degree is three.
 . Thus, its order is four.
. Thus, its order is four.






 and
and  in the differential equation, we get:
in the differential equation, we get:



 and
and  in the L.H.S. of the given differential equation, we get:
in the L.H.S. of the given differential equation, we get:



 in the L.H.S. of the given differential equation, we get:
in the L.H.S. of the given differential equation, we get:


 in the L.H.S. of the given differential equation, we get:
in the L.H.S. of the given differential equation, we get:
 where a is an arbitrary constant.
where a is an arbitrary constant.




 is the general solution of differential equation
is the general solution of differential equation , where c is a parameter.
, where c is a parameter.

 in equation (1), we get:
in equation (1), we get:
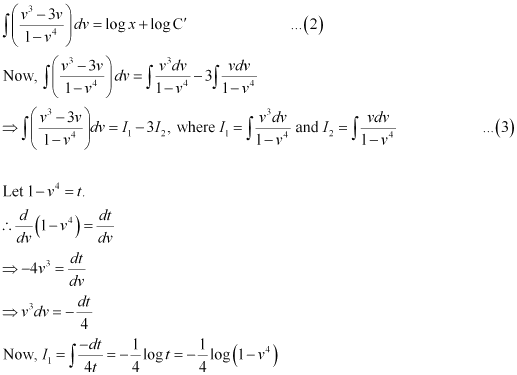










 is given by (x y 1) = A (1 – x – y – 2xy), where A is parameter
is given by (x y 1) = A (1 – x – y – 2xy), where A is parameter



 whose differential equation is,
whose differential equation is, 




 in equation (1), we get:
in equation (1), we get:

 , given that y = 1 when x = 0
, given that y = 1 when x = 0



 in equation (2), we get:
in equation (2), we get:





 , given that y = – 1, when x = 0 (Hint: put x – y = t)
, given that y = – 1, when x = 0 (Hint: put x – y = t)
 in equation (1), we get:
in equation (1), we get:






 , given that y = 0 when
, given that y = 0 when 





 in equation (1), we get:
in equation (1), we get:
 , given that y = 0 when x = 0
, given that y = 0 when x = 0







 is
is

 is
is





 is
is

























