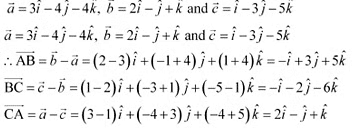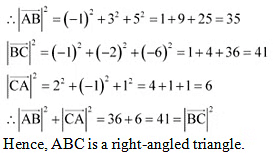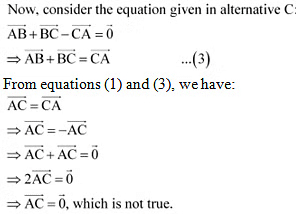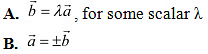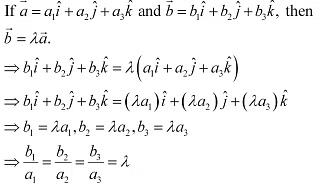Q6: Compute the magnitude of the following vectors:

Ans: The given vectors are:

Q7: Write two different vectors having same magnitude.
Ans:

Q8: Write two different vectors having same direction.
Ans:

Q9: Find the values of x and y so that the vectors  are equal.
are equal.
Ans: The two vectors will be equal if their corresponding components are equal.
Hence, the required values of x and y are 2 and 3 respectively.
Q10: Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
Ans: The vector with the initial point P (2, 1) and terminal point Q (–5, 7) can be given by,

Hence, the required scalar components are –7 and 6 while the vector components are
Q11: Find the sum of the vectors 

Q12: Find the unit vector in the direction of the vector 
Ans: The unit vector in the direction of vector is given by .

Q13: Find the unit vector in the direction of vector , where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
Ans: The given points are P (1, 2, 3) and Q (4, 5, 6).

Q14: For given vectors, and , find the unit vector in the direction of the vector
Ans:

Q15: Find a vector in the direction of vector 
Ans:

Q16: Show that the vectors are collinear.
are collinear.
Ans:

Q17: Find the direction cosines of the vector 
Ans:

Q18: Find the direction cosines of the vector joining the points A (1, 2, –3) and B (–1, –2, 1) directed from A to B.
Ans: The given points are A (1, 2, –3) and B (–1, –2, 1).

Q19: Show that the vector is equally inclined to the axes OX, OY, and OZ.
Ans:

Therefore, the direction cosines of
Now, let α, β, and γbe the angles formed by with the positive directions of x, y, and z axes.
Then, we have
Hence, the given vector is equally inclined to axes OX, OY, and OZ.
Q20: Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are  respectively, in the ration 2:1
respectively, in the ration 2:1
Ans: The position vector of point R dividing the line segment joining two points
P and Q in the ratio m: n is given by:
i. Internally:

(i) The position vector of point R which divides the line joining two points P and Q internally in the ratio 2:1 is given by,

(ii) The position vector of point R which divides the line joining two points P and Q externally in the ratio 2:1 is given by

Q21: Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Ans: The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, – 2) is given by,

Q22: Show that the points A, B and C with position vectors  ,
,  respectively form the vertices of a right angled triangle.
respectively form the vertices of a right angled triangle.
Ans: Position vectors of points A, B, and C are respectively given as


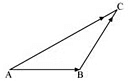
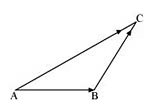
Q23: In triangle ABC which of the following is not true:



Ans: On applying the triangle law of addition in the given triangle, we have:



Hence, the equation given in alternative C is incorrect.
The correct answer is C.
Q24: If are two collinear vectors, then which of the following are incorrect

C. the respective components of are proportional
D. both the vectors have same direction, but different magnitudes
Ans: If are two collinear vectors, then they are parallel.

Thus, the respective components of are proportional.
However, vectors can have different directions.
Hence, the statement given in D is incorrect.
The correct answer is D.
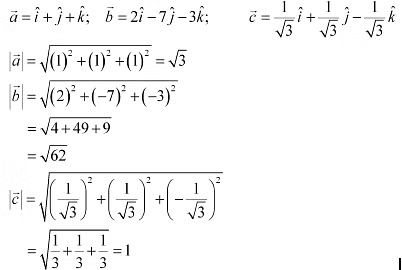
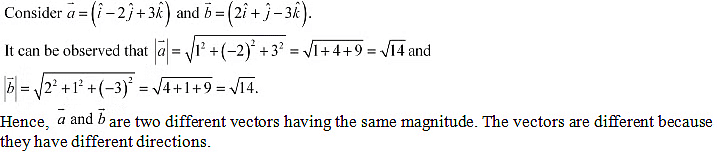
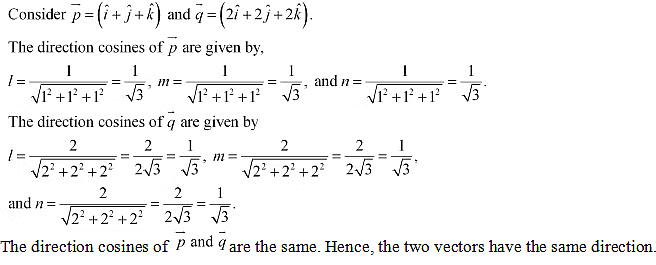
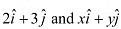 are equal.
are equal.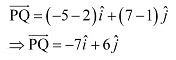
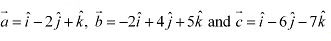
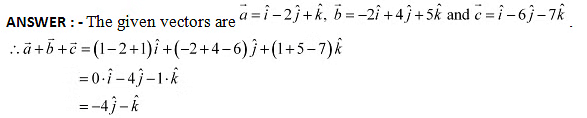
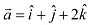
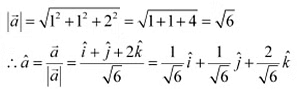
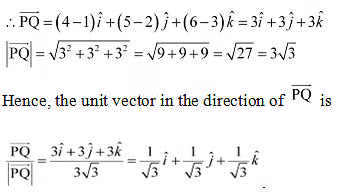
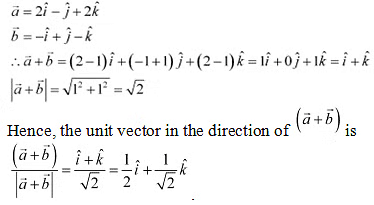
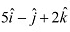
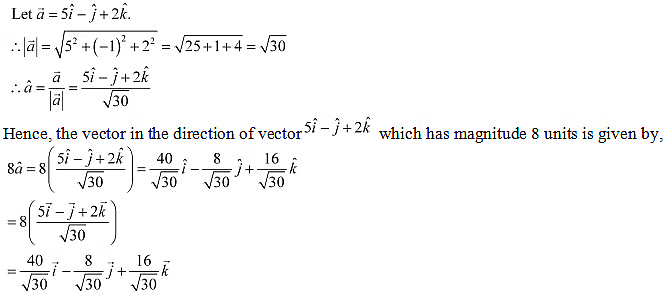
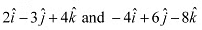 are collinear.
are collinear.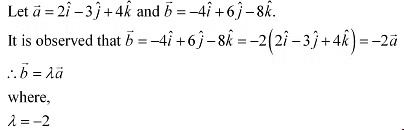
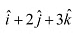
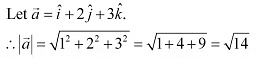
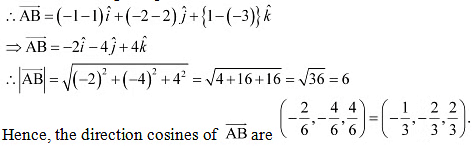
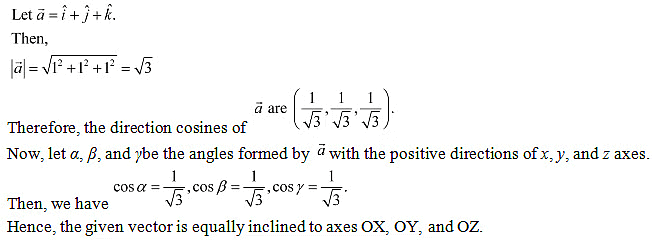
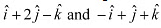 respectively, in the ration 2:1
respectively, in the ration 2:1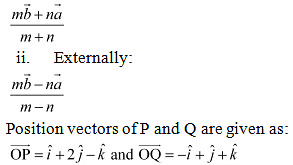
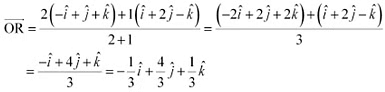
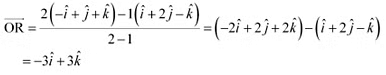
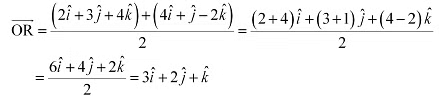
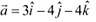 ,
, 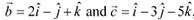 respectively form the vertices of a right angled triangle.
respectively form the vertices of a right angled triangle.