Important Solved Questions for CAT: Venn Diagrams | Logical Reasoning (LR) and Data Interpretation (DI) PDF Download
Q1: Sonu started a new business with accounts in two different banks (i.e. Axis and SBI).He deposited the earnings of each day in either of the two banks. However he does not deposit his earnings in both the banks simultaneously on any given day. However somehow he could not carry the business for long and had to shut it down. Find the total no of days Sonu carried on the business if…
1) He did not deposited in axis bank on 20 days and in SBI on 24 days.
2) He deposited on either axis bank or SBI on 28 days.
(a) 36
(b) 18
(c) 13
(d) 24
Ans: (a)
Sol:
Let the total No. of days Sonu deposited the earnings in Axis bank be ‘n(a)’ and that in SBI be ‘n(b)’
Now,
Total no of days he carried on the business = n(a) + n(b) – n(a∩b) + Neither (Days he didn’t earned)
Since on any given day he does not deposit in both the bank accounts
n(a∩b) = 0
Hence,
Total no of days he carried on the business = n(a) + n(b) + Neither (Days he didn’t earned)
Now,
A/Q
Total – n(a) = 20……………………………(1)
Total – n(b) = 24……………………………(2)
n(a) + n(b) = 28………………………………(3)
Solving the 3 equations we get,
n(a) = 16
n(b) = 12
Total = 36
Hence the total number of days he carried on the business = 36
The question is "Find the total no of days Sonu carried on the business if…"
Hence, the answer is "36".
Q2: During the placement season of a class, 21 students got shortlisted for company A, 26 got shortlisted for Company B and 29 got shortlisted for company C and 14 students got shortlisted for both A and B, 12 students got shortlisted for A and C and 15 for both B and C. All the companies shortlisted 8 students from the class. Then what is the ratio of number of students who got shortlisted for only B and number of students who got shortlisted for only C?
(a) 1:1
(b) 1:2
(c) 2:3
(d) 3:2
Ans: (b)
Sol: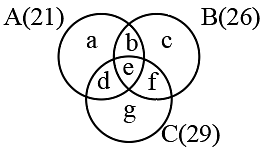
Given e = 8
Number of students shortlisted for A and B is 14
e + b = 14
b = 6
Number of students shortlisted for A and C is 12
e + d = 12
d = 4
Number of students shortlisted for B and C is 15
e + f = 15
f = 7
Given
Number of students shortlisted for B is 26
b + f + e + c = 26
6 + 7 + 8 + c = 26
c = 5
Number of students shortlisted for C is 29
d + e + f + g = 29
g = 10
Number of students shortlisted for A is 21
b + e + d + a = 21
a = 3
Number of students shortlisted for only B = c = 5
Number of students shortlisted for only C = g = 10
Ratio = 5:10 = 1:2
Answer is option B
Q3: Set A comprises all three digit numbers that are multiples of 5, Set B comprises all three–digit even numbers that are multiples of 3 and Set C comprises all three–digit numbers that are multiples of 4. How many elements are present in {A ∪ B ∪ C}?
(a) 420
(b) 405
(c) 555
(d) 480
Ans: (a)
Sol: This question is more of a Number Systems question than a Set Theory one!!
Set A = {100, 105, 110, ….995} ↦ {5 * 20, 5 * 21, ….. 5 * 199} ↦ 180 elements.
Set B = {102, 108, 114, ……996} ↦ {6 * 17, 6 * 18, 6 * 19, ….. 6 * 166} ↦ 150 elements.
Set C = {100, 104, 108, …..996} ↦ {4 * 25, 4 * 26, ….. 4 * 249} ↦ 225 elements.
A ∩ B = {120, 150, 180, …..990} ↦ All 3-digit multiples of 30 ↦ 30 elements.
B ∩ C = {108, 120, 132, …..996} ↦ All 3-digit multiples of 12 ↦ 75 elements.
C ∩ A = {120, 140, 160, …..980} ↦ All 3-digit multiples of 20 ↦ 45 elements.
A ∩ B ∩ C = {120, 180, …..960} ↦ All 3-digit multiples of 60 ↦ 15 elements.
A ∪ B ∪ C = A + B + C – A ∩ B – B ∩ C – C ∩ A + A ∩ B ∩ C
= 180 + 150 + 225 – 30 – 75 – 45 + 15 = 420
Hence, the answer is "420".
Q4: The number of people (in lakhs) who read only one newspaper is
(a) 4.7
(b) 11.9
(c) 17.4
(d) 23.4
Ans: (b)
Sol: Given Readership of newspaper X = 8.7
only X + 2.5 + 0.5 + 1 = 8.7
only X = 4.7
Given Readership of newspaper Y = 9.1
only Y + 2.5 + 1.5 + 0.5 = 9.1
only Y = 4.6
Given Readership of newspaper Z = 5.6
only Z + 0.5 + 1 + 1.5 = 5.6
only Z = 2.6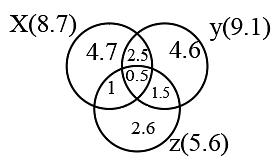
Number of people who read only one newspaper = 4.7 + 4.6 + 2.6 = 11.9 lakhs
Q5: Set P comprises all multiples of 4 less than 500. Set Q comprises all odd multiples of 7 less than 500, Set R comprises all multiples of 6 less than 500. How many elements are present in {P ∪ Q ∪ R}?
(a) 202
(b) 243
(c) 228
(d) 186
Ans: (a)
Sol: This question involves both Number Systems and Set Theory.
Set P = {4, 8, 12, ….496} ↦ 124 elements {all elements from 1 * 4 to 124 * 4}
Set Q = {7, 21, 35, 49,……497} ↦ {7 * 1, 7 * 3, 7 * 5, ….. 7 * 71} ↦ 36 elements.
Set R = {6, 12, 18, 24, …..498} ↦ {6 * 1, 6 * 2, 6 * 3, ….. 6 * 83} ↦ 83 elements.
Sets P and R have only even numbers; set Q has only odd numbers. So,
P ∩ Q = Null set
Q ∩ R = Null set
P ∩ Q ∩ R = Null set
So, If we find P ∩ R , we can plug into the formula and get P ∪ Q ∪ R
P ∩ R = Set of all multiples of 12 less than 500 = {12, 24, 36,…..492}
= {12 * 1, 12 * 2 , 12 * 3, …12 * 41} ↦ This has 41 elements
P ∪ Q ∪ R = P + Q + R – (P ∩ Q) – ( Q ∩ R) – (R ∩ P) + (P ∩ Q ∩ R)
P ∪ Q ∪ R = 124 + 36 + 83 – 0 – 0 – 41 + 0 = 202
The question is "How many elements are present in P ∪ Q ∪ R?"
Hence, the answer is "202".
Q6: In addition to the given information, which of the following information is NECESSARY and SUFFICIENT to compute the number of students choosing only E1, only E2 and only E3?
(a) Number of students choosing only E2, and number of students choosing both E2 and E3
(b) Number of students choosing both E1 and E2, number of students choosing both E2 and E3, and number of students choosing both E3 and E1
(c) Number of students choosing only E1, and number of students choosing both E2 and E3
(d) No extra information is necessary
Ans: (a)
Sol: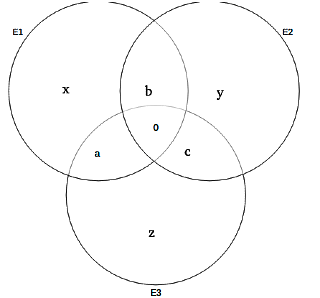
Given, a+b+c=50 and a+b+c+x+y+z=190 => x+y+z=140.
Also, let E1=k => E2=2k and E3=3k
E1+E2+E3= 6k=190+50=240 => k=40.
Option A: If the number of students choosing only E2, the number of students
choosing both E2 and E3, are given then the number of students who choose E2 and E1, E1 and E3 can be found. From this only E1, only E3 can be calculated.
Option B: knowing the number of students choosing both E1 and E2, the number of students
choosing both E2 and E3, and a number of students choosing both E3 and E1 is insufficient. This information is not enough to calculate the number of students who choose only E1, only E2, and only E3.
Option C: If x and c are known, we can’t find y and z.
Q7: John was born on Feb 29th of 2012 which happened to be a Wednesday. If he lives to be 101 years old, how many birthdays would he celebrate on a Wednesday?
(a) 3
(b) 4
(c) 5
(d) 1
Ans: (b)
Sol: Let us do this iteratively. Feb 29th 2012 = Wednesday => Feb 28th 2012 = Tuesday
Feb 28th 2013 = Thursday (because 2012 is a leap year, there will be 2 odd days)
Feb 28th 2014 = Friday, Feb 28th 2015 = Saturday, Feb 28th 2016 = Sunday, Feb 29th 2016 = Monday
Or, Feb 29th to Feb 29th after 4 years, we have 5 odd days.
So, every subsequent birthday, would come after 5 odd days.
2016 birthday – 5 odd days
2020 birthday – 10 odd days = 3 odd days
2024 birthday – 8 odd days = 1 odd day
2028 birthday – 6 odd days
2032 birthday – 11 odd days = 4 odd days
2036 birthday – 9 odd days = 2 odd days
2040 birthday – 7 odd days = 0 odd days. So, after 28 years he would have a birthday on Wednesday
The next birthday on Wednesday would be on 2068 (further 28 years later), the one after that would be on 2096. His 84th birthday would again be a leap year.
Now, there is a twist again, as 2100 is not a leap year. So, he does not have a birthday in 2100. His next birthday in 2104 would be after 9 odd days since 2096, or 2 odd days since 2096, or on a Thursday.
From now on the same pattern continues. 2108 would be 2 + 5 odd days later = 7 odd days later. Or, 2108 Feb 29th would be a Wednesday.
So, there are 4 occurrences of birthday falling on Wednesday – 2040, 2068, 2096 and 2108.
The question is "How many birthdays would he celebrate on a Wednesday?"
Hence, the answer is "4".
Q8: For a set S, we denote by S’, the complement of the set S. Let X, Y, Z be Sets such that 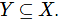 Which of the following is always true?
Which of the following is always true?
(a) 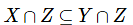
(b) 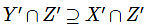
(c) 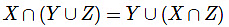
(d) 
Ans: (b)
Sol: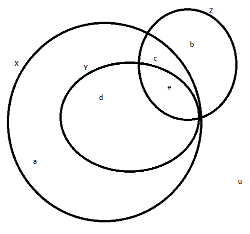
Consider the above Diagram
For option A 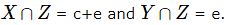 Hence option A is False
Hence option A is False
For option B 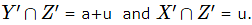 Option B is True
Option B is True
For option C 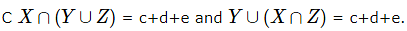 Option C is True
Option C is True
For option D  Option D is False.
Option D is False.
Q9: A´ is defined as the complement of A, as in, set of all elements that are part of the universal set but not in A. How many of the following have to be true?
i. n(A ∪ B)' = n(A' ∩ B')
ii. If A ∩ B=0}, then A' ∪ B'} is equal to the universal set
iii. If A ∪ B = universal set, then A' ∩ B' should be the null set.
iv. If A ⊂ B then A' ∪ B'=(A ∩ B)'
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (d)
Sol: Let's look at these statements one at a time:
i. n(A ∪ B)' =n(A' ∩ B')
This is a direct statement of De Morgan´s law. This is definitely true. Just to recap, De Morgan´s laws are as follows:
1. (A ∪ B)' =(A' ∩ B')
2. (A ∩ B)' =(A' ∪ B')
ii. A ∩ B=0, then A' ∪ B' is equal to the universal set
(A ∩ B)' =(A' ∪ B')
If A and B are disjoint sets, A ∩ B=0 and (A ∩ B)' is the universal set. This statement is correct.
iii. If A ∪ B = Universal Set, then A' ∩ B' should be the null set. This means (A ∪ B)' is the null set.
iv. If A ⊂ B, then A' ∪ B'= (A ∩ B)'
If A ⊂ B then A ∩ B=A.
This implies that (A ∩ B)'=A'
If A ⊂ B, then B' ⊂ A' and A' ∪ B'=A'
Thus A' ∪ B'= (A ∩ B)'. This statement is true.
The question is "How many of the following have to be true?"
Hence, the answer is all four statements are true.
Choice D is the correct answer.
Q10: Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
(a) 22
(b) 21
(c) 20
(d) 19
Ans: (c)
Sol: Now 23 students choose maths as one of their subject.
This means (MPC)+ (MC) + (PC)=23 where MPC denotes students who choose all the three subjects maths, physics and chemistry and so on.
So MC + PM =5 Similarly we have PC+ MP =7
We have to find the smallest number of students choosing chemistry
For that in the first equation let PM=5 and MC=0. In the second equation this PC=2
Hence minimum number of students choosing chemistry will be (18+2)=20 Since 18 students chose all the three subjects.
Q11: In class of 280 students, each student needs to choose between the three extra subject (i.e IT, Hindi and Sanskrit) offered along with the course. The students that choose each of these subjects are 160, 130, 110. The number of students who choose more than one of the three is 40% more than the number of students who choose all the three subjects If there are no students who choose none of the 3 subjects, how many students study all the three subjects?
(a) 40
(b) 50
(c) 80
(d) 100
Ans: (b)
Sol: In this question there are 260 students who are counted 160 + 130 + 110 = 400 times
This means there is an extra count of 400 – 280 = 120 students
Now, let the no. of students who choose all the three Subject be ‘n’
Then as per the question, the no. of students who choose more than 1 subject = 1.4 n
Thus, the no of students who study exactly 2 subjects = 1.4 n – n = 0.4 n
Extra count can occur from exactly 2 areas i.e from the ‘exactly two areas’ or ‘all three area’. We also know that a student placed in in all the three area will be counted 3 times, thus the extra count being 2 while in the case of exactly two students extra count is 1.
Thus the extra count from n students choose 3 subjects would be = 2 * n = 2n
And that of 0.4 student choose exactly 2 subjects = 1 * 0.4 n = 0.4n
Hence extra count = 120 = 2n + 0.4n
=> 120 = 2.4 n
=> 50 = n
Hence the no of students who choose all the three subjects = 50
The question is "How many students study all the three subjects?"
Hence, the answer is "50".
Choice B is the correct answer.
Q12: If 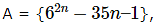 where n = 1,2,3,… and B = {35(n-1)}, where n = 1,2,3,… then which of the following is true?
where n = 1,2,3,… and B = {35(n-1)}, where n = 1,2,3,… then which of the following is true?
(a) Every member of A is in B and at least one member of B is not in A
(b) Neither every member of A is in B nor every member of B is in A
(c) Every member of B is in A.
(d) At least one member of A is not in B
Ans: (a)
Sol: If we carefully observe set A, then we find that 62n-35n - 1 is divisible by 35. So, set A contains multiples of 35. However, not all the multiples of 35 are there in set A, for different values of n.
for n=1. the value is 0, for n=2, the value is 1225 which is the 35th multiple of 3.
If we observe set B, it consists of all the multiples of 35 including 0.
So, we can say that every member of set A will be in B while every member of set B will not necessarily be in set A.
Hence, option A is the correct answer.
Q13: A factory has 80 workers and 3 machines. Each worker knows to operate atleast 1 machine. If there are 65 persons who knows to operate machine 1, 60 who knows to operate machine 2 and 55 who knows to operate machine 3,what can be the minimum number of persons who knows to operate all the three machines?
(a) 15
(b) 20
(c) 30
(d) 40
Ans: (b)
Sol: Let’s start with taking a random value for all three category. So let’s first take 40 for the all three category. Now 65 + 60 + 55 = 180, this means there is an extra count of 180 – 80 = 100.
Now as we know that the extra count occurs in the in the exactly two area and the all three area. So let’s try put the extra count in these area.
Trial 1 - Since 40 is already assumed to be in the all three area, it takes care of extra count of 40 x 2 = 80. Thus we are left with 20 as extra count which we have to place at the exactly two area
Thus in the above case our venn diagram will look as: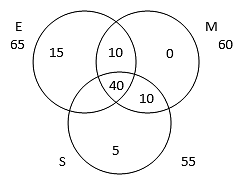 A close look in the figure tells us that we can further decrease the value of all the three area. A bit of logical thinking will bring us to the value 20. No value less than 20 can satisfy the conditions of the question. As there is no scope left for reallocating numbers left from one area to another in this case.
A close look in the figure tells us that we can further decrease the value of all the three area. A bit of logical thinking will bring us to the value 20. No value less than 20 can satisfy the conditions of the question. As there is no scope left for reallocating numbers left from one area to another in this case.
Hence the final venn diagram will look as: The question is "what can be the minimum number of persons who knows to operate all the three machines?"
The question is "what can be the minimum number of persons who knows to operate all the three machines?"
Hence, the answer is "20".
Q14: If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
(a) 23
(b) 26
(c) 96
(d) 93
Ans: (d)
Sol: It has been given that among 200 students, 105 like pizza and 134 like burger.
The question asks us to find out the number of students who can be liking only burgers among the given values.
The least number of students who like only burger will be obtained when everyone who likes pizza likes burger too.
In this case, 105 students will like pizza and burger and 134-105 = 29 students will like only burger. Therefore, the number of students who like only burger cannot be less than 29.
The maximum number of students who like only burger will be obtained when we try to separate the 2 sets as much as possible.
There are 200 students in total. 105 of them like pizza. Therefore, the remaining 95 students can like only burger and 134-95 = 39 students can like both pizza and burger. As we can see, the number of students who like burger cannot exceed 95.
The number of students who like only burger should lie between 29 and 95 (both the values are included).
93 is the only value among the given options that satisfies this condition and hence, option D is the right answer.
Q15: In Grand Oberoi hotel, 1160 guests are present currently. The hotel provides the following extra facilities: Gym, Swimming, Fun park, Food. During a regular survey the management team of Oberoi noticed something quite extraordinary about the extra facilities provided by them. They noticed that for every person who uses ‘F’ no. of facilities, there are exactly 3 persons who uses at least (F-1) no. of facilities, F = 2, 3, 4. They also found that the no. of persons who used no extra facilities is twice the no of person that used all the 4 facilities. Help the management team to find out how many persons used exactly 3 facilities.
(a) 40
(b) 60
(c) 80
(d) 100
Ans: (c)
Sol: Since, for every person who uses ‘F’ no of facilities, there are exactly 3 person who uses atleast (F-1) no. of facilities. If we take the no. of persons who uses all the four facilities to be ‘x’ then the no. of person who uses atleast 3 facilities will be 3x and so on.
The No. of persons who use exactly 3 facilities = 3x – x = 2x
Thus, the no. of persons who opt for various facilities can be summarized as follows: We also know that no of person who uses no facilities = twice of those who uses all the 4 facilities = 2x.
We also know that no of person who uses no facilities = twice of those who uses all the 4 facilities = 2x.
So according the above deductions we can clearly see that the number of person the hotel would be
x + 2x + 6x + 18x + 2x = 29 x = 1160
x = 40
Hence the number of person who uses exactly three science = 2x = 80
The question is "Help the management team to find out how many persons used exactly 3 facilities."
Hence, the answer is "80".
Q16: Referring to the previous question, what percentage of people watched all the three channels?
(a) 3.5%
(b) 0%
(c) 8.5%
(d) Cannot be determined
Ans: (d)
Sol: Applying AUBUC formula
Let x be the number who watch BBC and CNN and y be the number who watch all three channels.
100 = 80+22+15-(10+5+x)+y
x-y = 2
We cannot find the exact value of y.
Hence, the answer is “cannot be determined”.
Q17: In a class of 345 students, the students who took English, Math and Science are equal in number. There are 30 students who took both English and Math only, 26 who took both Math and Science only, 28 who took Science and English only and 14 who took all the 3 subjects.There are 43 students who didn’t take any of the subjects. Answer the following question according to the data given above.
What percent of students did not take Science?
(a) Less than 55%
(b) approx. 59%
(c) 72 %
(d) 79%
Ans: (b)
Sol: Let total no of students who took English be x
Then students who took math, science will also be x
Now let’s draw the Venn diagram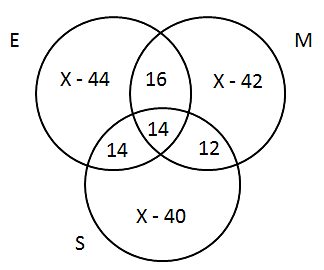 E U M U S = 345 – 43 (Neither of the subjects)
E U M U S = 345 – 43 (Neither of the subjects)
E U M U S = E + M + S – E ∩ M - E ∩ S - S ∩ M + E ∩ M ∩ S
=> 302 = 3x - 84 + 14
=> 302 + 84 – 14 = 3x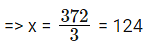
Thus the total no of students who took English as a subject = 124
Consequently the Venn diagram becomes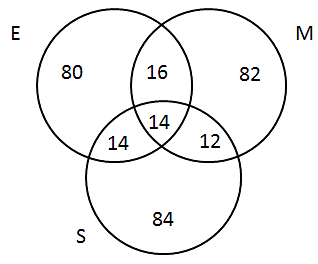
Again,
The students who has taken only one subject = E U M U S - E ∩ M - E ∩ S - S ∩ M - E ∩ M ∩ S
= 302 - 16 - 14 - 14 - 12 = 246
The students who took English and Math but not science = only E + Only M + E ∩ M
= 80 + 82 + 16 = 178
Percent of students who took English and Math but not science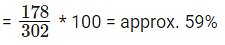
Q18: What is the maximum percentage of people who can watch all the three channels?
(a) 12.5%
(b) 8.5%
(c) 15%
(d) Data insufficient
Ans: (b)
Sol: Let a be the number who watch only one channel, b be the number who watch only 2 channels and c be the number who watch all channels.
a+b+c = 100
a+2b+3c = 80+22+15 =117
Subtracting both equations,
b+2c = 117-100 = 17
Maximum c occurs when b = 0
2c = 17
c = 8.5
Q19: In a class of 345 students, the students who took English, Math and Science are equal in number. There are 30 students who took both English and Math, 26 who took both Math and Science, 28 who took Science and English and 14 who took all the 3 subjects.There are 43 students who didn’t take any of the subjects. Answer the following question according to the data given above.
How many students have taken English as a subject?
(a) 286
(b) 124
(c) 246
(d) 108
Ans: (b)
Sol: Let total no of students who took English be x
Then students who took math, science will also be x
Now let’s draw the Venn diagram
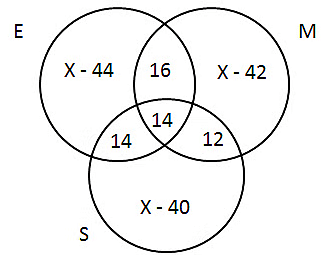
E U M U S = 345 – 43 (Neither of the subjects)
E U M U S = E + M + S – E ∩ M - E ∩ S - S ∩ M + E ∩ M ∩ S
=> 302 = 3x - 84 + 14
=> 302 + 84 – 14 = 3x
Thus the total no of students who took English as a subject = 124
Consequently the Venn diagram becomes Again,
Again,
The students who has taken only one subject = E U M U S - E ∩ M - E ∩ S - S ∩ M - E ∩ M ∩ S
= 302 - 16 - 14 - 14 - 12 = 246
The students who took English and Math but not science = only E + Only M + E ∩ M
= 80 + 82 + 16 = 178
Percent of students who took English and Math but not science
The question is "How many students have taken English as a subject?"
Hence, the answer is "124".
Q20: How many schools had none of the three viz., laboratory, library or play – ground?
(a) 20
(b) 5
(c) 30
(d) 35
Ans: (d)
Sol: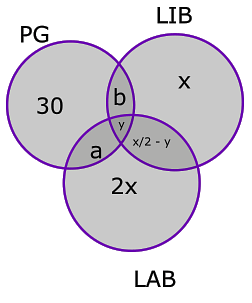 The diagram for this question has been shown:
The diagram for this question has been shown:
Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35
It has been given that the schools having playground don’t have a Library or Laboratory.
Here a = b = y = 0
7x/2 = 35
x = 10
Total number of schools having at least one of PG, LIB or LAB = 30+2x+x+x/2 = 30+3x+x/2 = 30+30+5 = 65
Number of schools having neither of the three = 100-65 = 35
|
88 videos|119 docs|91 tests
|
FAQs on Important Solved Questions for CAT: Venn Diagrams - Logical Reasoning (LR) and Data Interpretation (DI)
| 1. What is a Venn diagram and how is it used in the CAT exam? |  |
| 2. How can Venn diagrams be used to solve CAT exam questions? |  |
| 3. Can Venn diagrams be used to solve questions from other topics in CAT? |  |
| 4. Are there any specific strategies or tips to solve Venn diagram questions in the CAT exam? |  |
| 5. Are there any shortcuts or tricks to solve Venn diagram questions quickly in the CAT exam? |  |
|
88 videos|119 docs|91 tests
|

|
Explore Courses for CAT exam
|

|

















