Important Formulas: Number Series | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| Number Series Formulas |

|
| Formulas for Number Series |

|
| Types of number series |

|
| Square up and Square Add up Series |

|
Number Series Formulas
A number series is a progression of numbers arranged based on a specific system or rule, without adhering to a particular order. The task involves identifying the underlying system or rule governing a given series and using it to determine the subsequent numbers.
For Example : 3, 9, 27, 81 ?
It is Geometric series.
Each term is Multiplied by 3.
So , 81 x 3 = 243

Formulas for Number Series
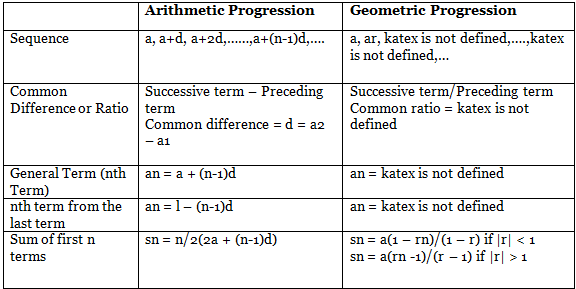
Types of number series
Types of Number Series is given below:
- Arithmetic Sequence: A sequence in which every term is created by adding or subtracting a definite number to the preceding number is an arithmetic sequence.
- Geometric Sequence: A sequence in which every term is obtained by multiplying or dividing a definite number with the preceding number is known as a geometric sequence.
- Harmonic Sequences: A series of numbers is said to be in harmonic sequence if the reciprocals of all the elements of the sequence form an arithmetic sequence.
- Fibonacci Numbers: Fibonacci numbers form an interesting sequence of numbers in which each element is obtained by adding two preceding elements and the sequence starts with 0 and 1.
Add Up Series
Add up Series +
- Probability of asking – Very Low
- Difficulty – Low
- Reason – to Introduce Concept
These problems are never asked they are very easy, we are talking about them to introduce the number series from basic.
- Rule – Just Add a number ‘N’ to the last number.
- E.g. – 5, (5 + 3 = 8), (8 + 3 = 11), ( 11 + 3= 14) ….
- Result – 5, 8, 11, 14, 17 ……..
Add up Series –
- Probability of asking – Very Low
- Difficulty – Low
- Reason – to Introduce Concept
- Rule : Just Add a number ‘N’ to the last number.
- E.g. : 4, (4 – 5 = (-1)), (-1 -5 = -6), ( -6 – 5 = -11) ….
- Result : 4, -1, -6, -11, -16 ……..
Square up and Square Add up Series
Square up and Square Add up Series +
Square up +(Easy to Identify)
- Rule – For a number X and for a number a where a = 1, 2, 3….. do next number = x + a2
- E.g. – 5
- 5 + 22 = 5 + 4 = 9
- 9 + 32 = 9 + 9 = 18
- 18 + 42 = 18 + 16 = 34
- 34 + 52 = 34 + 25 = 59
- Result – 5, 9, 18, 34, 59 …..
Square up Add up +(Hard to Identify)
- Rule – For a number X and for a number a where a = 1, 2, 3….. do next number = x + a2 + b for b some pattern.
- E.g. – 5
- 5 + 22 + 3 = 5 + 4 + 3 = 12
- 12 + 32 + 3 = 12 + 9 + 3 = 24
- 24 + 42 + 3 = 24 + 16 + 3 = 43
- 43 + 52 + 3 = 43 + 25 + 3 = 71
- Result – 5, 12, 24, 43, 71 …..
Square up Step up +(Very hard to identify not asked mostly unless paper is very tough)
- Rule – For a number X and for a number a where a = 1, 2, 3….. do next number = x + katex is not defined + b for b some pattern.
- E.g. – 5
- 5 + katex is not defined + 3 = 5 + 4 + 3 = 12
- 12 + katex is not defined + 8(3+5) = 12 + 9 + 8 = 29
- 29 + katex is not defined +13(8+5) = 29 + 16 + 13 = 58
- 58 + katex is not defined + 18(13+5) = 58 + 25 + 18 = 101
- Result – 5, 12, 29, 58, 101 ..
Square up and Square Add Up Series -
Same for Step up Series +, but instead of adding, Subtract.
Examples of Number Series
Example 1: Find the missing number? 99, 121, 143, ___, 187, 199 .
(a) 170
(b) 165
(c) 158
(d) 172
Ans: (b)
The given series is an AP with first term as 99 and common difference as 22.
Example 2: Find the next term in the series : 51,52,53,55,58,63,____.
(a) 69
(b) 77
(c) 81
(d) 71
Ans: (d)
Fibonacci series is added to each term.
51 + 0 =51
51 + 1=52
52 + 1=53
53 + 2=55
55 + 3=58
58 + 5=63
63 + 8=71
Example 3: Find the missing terms? 97,122,107,132,__,__.
(a) 117,142
(b) 122,112
(c) 141,131
(d) 121,131
Ans: (a)
This series is a result of alternate +25 and -15.
97 + 25=122
122 – 15=107
107 + 25=132
132 – 15=117
117 + 25=142
So, the next two terms are 117 and 142.
Example 4: Fill the missing term in the series
100, 92, 86 ,82, 74, 68, 64, 56, 50, __, ___.
(a) 44, 36
(b) 40, 34
(c) 46, 38
(d) 44, 32
Ans: (c)
The number series are in successive subtraction series of – 8, -6, -4 and then again -8,-6,-4.
So, the next terms after 50 will be 50-4=46 and 46-8=38.
Example 5: Select the missing number from the given responses.
19, 35, 67, 131, 259, 515, ?
(a) 1281
(b) 1291
(c) 1071
(d) 1027
Ans: (d)
11 × 2 – 3 = 19
19 × 2 – 3 = 35
35 × 2 – 3 = 67
67 × 2 – 3 = 131
131 × 2 – 3 = 259
259 × 2 – 3 = 515
515× 2 – 3 = 1027
|
342 videos|310 docs|185 tests
|




















