Important Formulas: Boats and Streams | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
The boat and stream concept is one of the most common topics based on which questions are asked in the various Government exams conducted in the country.
The boat and stream questions are asked in the quantitative aptitude section of the Government exams and the weightage of questions mostly varies between 1-3 marks.
Boat and Stream – Concept
There are a variety of subconcepts that are related to answering questions based on boat and streams concept. Given below are the four terms which are important for a candidate to know to understand the concept of streams.
- Stream: Refers to the moving water within a river.
- Upstream: When a boat moves against the stream's direction, it's considered to be going upstream. The boat's effective speed in this situation is termed as the upstream speed.
- Downstream: When a boat moves with the stream's direction, it's considered to be going downstream. The boat's effective speed here is referred to as the downstream speed.
- Still Water: This scenario describes water that is not moving. The speed of the water in this case is assumed to be zero.
Formula for Upstream
(U - V) km/hr, where U represents the speed of the boat in still water, and V represents the speed of the stream.
Formula for Downstream
(U + V) km/hr, where U stands for the speed of the boat in still water, and V stands for the speed of the stream.
Formulas for Boats and Streams Questions with Basic Concepts
What is Downstream?
Downstream refers to the direction of water flow in relation to an object. When the object or body is moving in the same direction as the stream, it is termed as downstream.
What is Upstream?
Upstream is also associated with the direction of water flow in relation to an object. When the object or body is moving in the opposite direction to the stream, it is designated as upstream. Problems involving boats and streams are rooted in the principles of time, speed, and distance, but certain modifications are required for such scenarios. These problems can manifest in two variations.
Below are the best formulas of boats and Streams problems in seconds.
Basic Formulas for Upstream and Downstream
Basic Formula 1
If the speed of a boat in still water is u km/hr and the speed of the stream is v km/hr, then
Speed downstream = (u + v) km/hr
Speed upstream = (u – v) km/hr.
Basic Formula 2
If the speed downstream is a km/hr and the speed upstream is b km/hr, then
Speed in still water
Rate of stream
Additional Formula 1
Lets Assume that a man can row at the speed of x km/hr in still water and he rows the same distance up and down in a stream which flows at a rate of y km/hr. Then his average speed throughout the journey is :
Additional Formula 2
Let the speed of a man in still water be x km/hr and the speed of a stream be y km/hr. If he takes t hours more in upstream than to go downstream for the same distance, the distance travelled is
Additional Formula 3
A man rows a certain distance downstream in t1 hours and returns the same distance upstream in t2 hours. If the speed of the stream is y km/hr, then the speed of the man in still water
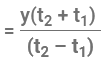
Additional Formula 4
A man can row a boat in still water at x km/hr in a stream flowing at y km/hr. If it takes him t hours to row a place and come back, then the distance between the two places is
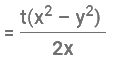
Miscellaneous Examples
Example 1: A person can swim in water with a speed of 13 km/hr in still water. If the speed of the stream is 4 km/hr, what will be the time taken by the person to go 68 km downstream?
Solution:
Downstream Speed = (13+4) km/hr = 17 km/hr
To travel 68 km downstream.
Time taken = 68/17 = 4 hours
Example 2: A woman can row upstream at 16 km/hr and downstream at 26 km/hr. What is the speed of the stream?
Solution:
According to the formula,
Speed of the stream = ½ (Downstream Speed – Upstream Speed)
Speed of the stream = ½ (26-16) = ½ × 10 = 5 km/hr
Example 3: A boat is moving 2 km against the current of the stream in 1 hour and moves 1 km in the direction of the current in 10 minutes. How long will it take the boat to go 5 km in stationary water?
Solution:
Downstream = (1/10 × 60) = 6 km/hr
Upstream = 2 km/hr
Speed in still water = ½ (6+2) = 4 km/hr
So, the time is taken by the boat to go 5km in stationary water = 5/4 hrs = 1 ¼ hrs = 1 hr 15 minutes
Example 4: The speed of a swimmer in still water is 12 km/hr. It takes 6 hrs to swim to a certain distance and return to the starting point. The speed of current is 4km/hr. Find the distance between the two points.
Solution:
Let distance = D
Downstream time = t1; Downstream Speed = 1/2*(12+4) = 8 km/hr
Upstream Time = t2; Upstream Speed = 1/2*(12-4) = 4 km/hr
Total time = t1 + t2
6 = (D/Upstream speed) + (D/Downstream speed)
6 = D/8 + D/4
D = 16 km
Example 5: A woman can swim in water with a speed of 15 km/hr in still water. If the speed of the stream is 4 km/hr, what will be the time taken by the person to go 76 km downstream?
Solution:
Downstream Speed = (15+4) km/hr = 19 km/hr
To travel 76 km downstream.
Time taken = 76/19 = 4 hours
|
1365 videos|1312 docs|1010 tests
|
FAQs on Important Formulas: Boats and Streams - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is the formula for calculating the speed of a boat in upstream? |  |
| 2. How do you calculate the speed of a boat in downstream? |  |
| 3. What are the basic formulas for solving boats and streams problems? |  |
| 4. What is the additional formula for calculating the time taken to travel a certain distance in still water? |  |
| 5. How can the concept of boats and streams be applied in real-life situations? |  |
|
1365 videos|1312 docs|1010 tests
|

|
Explore Courses for SSC CGL exam
|

|





















