Important Formulas: Coordinate Geometry | Quantitative Aptitude for SSC CGL PDF Download
What is Coordinate Geometry?
Coordinate geometry is a branch of geometry that defines the position of points on the plane using an ordered pair of numbers, commonly known as coordinates.

Coordinate Geometry Formulas and Basic Concept
- The origin is the point where the x and y-axes intersect, with both x and y coordinates being 0 at this point.
- Positive values are found on the right side of the x-axis, while negative values are on the left side.
- Similarly, on the y-axis, values above the origin are positive, and values below the origin are negative.
Formulas Required for Solving Coordinate Geometry Questions.
- Distance between two points A(x1, y1) and B(x2, y2)
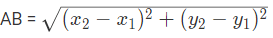
- Slope of line when two points are given (x1, y1) and (x2, y2)
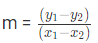
- Slope of line when linear equation is given ax + by = c =>
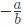
- Midpoint
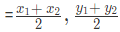
- The co-ordinates of a point R(x,y) that divides a line segment joining two points A(x1, y1) and B(x2, y2) internally in the ratio m:n is given by

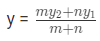
- The co-ordinates of a point R(x, y) that divides a line segment joining two points A(x1, y1) and B(x2, y2) externally in the ratio m:n is given by
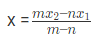
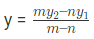
- Centroid of a triangle with its vertices (x1,y1), (x2,y2), (x3,y3)
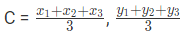
- Area of a Triangle with its vertices A(x1,y1), B(x2,y2), C(x3,y3)
- Division of a line segment by a point
If a point p(x, y) divides the join of A(x1, y1) and B(x2, y2), in the ratio m: n, then
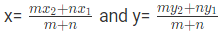
The equation of a line in slope intercept form is Y= mx+ c, where m is its slope.
The equation of a line which has gradient m and which passes through the point (x1, y1) is = y – y1 = m(x – x1).
Some Examples Using Above Formulas
Q1: Given two points A(2, 5) and B(6, 9), find the Distance between points A(2, 5) and B(6, 9)
Ans: Distance between points A(2, 5) and B(6, 9):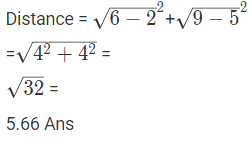

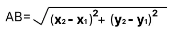
Q2: If the slope of a line is -2/3 and it passes through the point (2, 5), find the equation of the line in point-slope form.
Ans: Equation of the line passing through points P(3, 8) and Q(5, -2):
Using the point-slope form: y – y1 = m(x – x1)
y – 8 = -5(x – 3)
y – 8 = -5x + 15
y = -5x + 23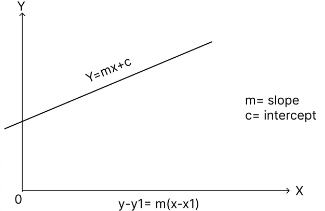
Q3: A rectangle has vertices at points A(1, 1), B(5, 1), C(5, 3), and D(1, 3). Determine its area and perimeter.
Ans: Rectangle with vertices at points A(1, 1), B(5, 1), C(5, 3), and D(1, 3):
Area = Length * Width Length =
Distance between points B and C:
Length = √((5 – 5)2 + (3 – 1)2) = √(0 + 4) = √4 = 2
Width = Distance between points A and B:
Width = √((5 – 1)2 + (1 – 1)2) = √(16 + 0) = √16 = 4 Area = 2 * 4 = 8 square units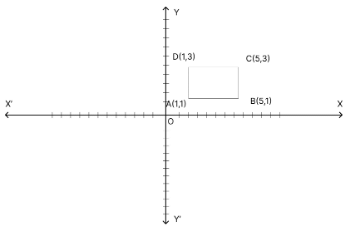
Q4: Determine the equation of the circle with center C(2, -1) and a radius of 5.
Ans: Equation of the circle with center C(2, -1) and radius 5:
The equation of a circle with center (h, k) and radius r is (x − h)2 + (y − k)2 = r2
For this circle: = (x − h)2 + (y−(−1)2 = r2 = 52 (x – 2)2 + (y + 1)2 = 25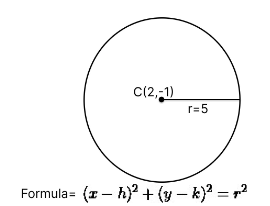
Q5: Given the points A(3, 6), B(8, 6), and C(5, 2), find the area of the triangle ABC.
Ans: Area of triangle ABC with vertices A(3, 6), B(8, 6), and C(5, 2):
Area = 1/2 |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
Area = 1/2 |3(6 – 2) + 8(2 – 6) + 5(6 – 6)|
Area = 1/2 |12 – 24 + 0|
Area = 1/2 |-12|
Area = 6 square units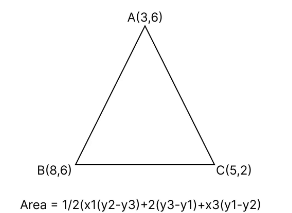
|
317 videos|299 docs|156 tests
|
















