Solved Examples: Time & Work | Quantitative Aptitude for SSC CGL PDF Download

Time

Time, within the framework of work, is the quantification of duration and advancement that dictates the order of events and tasks.

Work

Work, within the context of work and time, pertains to the physical or mental exertion applied to complete a task or attain a goal within a designated timeframe.

The essential questions that may be posed in the examination concerning the topic of Time and Work are outlined below:

• Acquaint yourself with the fundamental concepts of time and work, including the calculation of work done and time taken.
• Comprehend the basic formula: Work = Rate × Time.
• Reciprocal Work Rate: Familiarize yourself with addressing situations where an individual's work rate is expressed in terms of the time taken to complete the work (e.g., "Raj can do a job in 10 days," indicating Raj's work rate is 1/10 of the job per day).
• Practice problems involving multiple individuals collaborating or working at different rates to accomplish a task.
• Fractional Work: Learn how to handle scenarios where a fraction of the work is completed (e.g., "A completes half the work").
• Work Efficiency: Grasp the concept of efficiency and its connection to work rates.

Rules on Time and Work

• Let’s consider  M1 number of individuals are able to complete W1 amount of work within D1 days whereas M2 number of individuals  are able to complete W2 amount of work in D2 days, then the formula used will be:
  
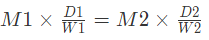
• If the individuals are having productivity of E1 and E2 individually, then the formula used to calculate the same will be:
  
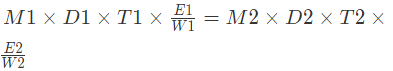
• If person A is able to do a part of work in ‘n’ number of days, then the work done by A in a single day is equals to 1/n
• If person X might complete an amount of work in D1 number of days as well as person Y is able to complete the similar amount of work in D2 number of days then person X and person Y together can do the similar type of work in:
  
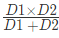
• Considering that person X is twice efficient worker as person Y, then person X would be taking half of the time occupied by person Y to do a similar amount of work.
• If person X along with person Y can together complete a part of work in D1 number of days as well as person X unaccompanied is able to complete it in D2 number of days, then person Y can alone complete the work in:
  

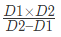
Examples 

Example 1: Sam can finish a task is 12 days, and Adam can finish it in 15 days. Calculate how much time together they will take to complete the same job?
(a) 20 / 3
(b) 16 / 3
(c) 9 / 2
(d) 18 / 7
Ans: (a)
Sam’s 1 day effort = 1/12
Adam’s 1-day effort = 1/15
1 day effort of both of them = 1/12 + 1/15 = 3/20
Therefore, together they can finish the task in = 20/3 days
Hence Option A is the correct one.

Example 2: George and Victor can finish making a painting in 12 hours, Victor and Sam in 15 hours, Sam and George in 20 hours. Find in how many hours will they together finish the painting?
(a) 21
(b) 10
(c) 21/2
(d) 11
Ans: (b)
George and Victor, one hour work, = 1/12
Victor and Sam one hour work = 1/15
Sam and George one hour work = 1/20
George, Victor, and Sam’s one hour work = (1/2)(1/12 + 1/15 + 1/20) = 1/10
Therefore, George, Victor, and Sam can finish the painting in 10 hours.

Example 3: M can do a task in 25 days, and S can finish a similar job in 20 days. They work as one for five days and M goes away. Calculate the days required by S to do the work then?
(a) 12
(b) 11
(c) 17
(d) 21.5
Ans: (b)
M and S 5 days’ work = 5(1/25 + 1/20) = 9/20
Work left= 1 – 9/20 = 11/20
Now, 1/20 work is finished by S in 1 day.
Therefore, 11/20 work will be finished by S in 11 days

Example 4: Jack is three times as good as Rose. Jack can finish a task in 60 days less than Rose. Calculate the time in which they can complete the job together.
(a) 43/3
(b) 45/2
(c) 47/2
(d) 49/2
Ans: (b)
Let us assume that Rose can do the job in x days.
Then, Jack can do the job in (x -60) days.
Therefore, time taken by Jack = times of Rose/3
Therefore, x-60 =x/3
⇒ 3x – 180 = x
⇒ x = 90 days
Time taken by Rose = 90 days
Time taken by Jack = 30 days
Therefore, Rose and Jack’s one day work =(30 + 90)/(30 x 90) = 2/45
Hence, they can complete the same work together in  45/2 days.
Therefore option B is the correct one.

Example 5: Jack and Vinny can finish their target in 12 days. Vinny and Sid together can complete the goal in 15 days. If Jack is twice as good as Sid, calculate the number of days required by Vinny alone to finish the target?
(a) 21
(b) 22
(c) 25/2
(d) 20
Ans: (d)
Let the one day work by jack is “x” ,sid is '2x’ and that of vinay be’v’
2x+v = 1/12……………..(1)
v+x = 1/15…………….(2)
Now, from (1) - (2) we get
X = 1/60
There for
v=1/12 – 1/30
= 1/20
The no of days = 20

Example 6: Max and Samantha can together finish the project in 12 days. If Samantha alone takes 30 days to complete, then calculate the days in which Max will finish the project alone?
(a) 25
(b) 20
(c) 16
(d) 19
Ans: (b)
Max and Samantha together work time = 12
Max and Samantha one-day effort = 1/12
Samantha’s one-day effort = 1/30
Max one day effort = 1/12 – 1/30 = 1/20
Therefore, Max will take 20 days to finish the project.
Hence Option B is the correct one.

Example 7: Mary is three times as good as Jonny. If they finish a task together in 15 days, calculate the days taken by Mary alone to complete the work.
(a) 20
(b) 25
(c) 30
(d) 17
Ans: (a)
One day work by Mary: One day work by Jonny = 3:1
(Mary + Jonny)it's one-day work = 1/15
Now, when we divide 1/15 in the ratio of 3:1
Therefore, Mary’s one day work = (1/15) x (3/4) = 1/20
Hence, Mary can alone finish it in 20 days.

Example 8: Max can finish writing one chapter in 2 days. While Alex can do the same chapter in 5 days, calculate the number of days taken them together to complete the chapter?
(a) 5/9
(b) 1/2
(c) 10/7
(d) 8/11
Ans: (c)
Time taken by Max = 2 days
The effort did by Max in one day = 1/2
Days have taken by Alex = 5 days
The effort did by Alex in one day = 1/5
Thus, together they can complete work = (1/2) + (1/5) =7/10
Therefore, time required 10/7 days

Example 9: Mike and Nik can finish a project in 45 days and 40 days individually. Both of them started the project together, but Mike quits subsequently by some days, and Nik finishes the outstanding in 23 days. Find in how many days Mike quits?
(a) 8/3
(b) 7/2
(c) 9
(d) 9/5
Ans: (c)
Nik’s work after Mike quits = 23 * 1/40 = 23/40
Outstanding work = 1 – 23/40 = 17/40
Mike and Nik’s one day effort = 1/45 + 1/40 = 17/360
Therefore, 17/360 work done by Mike and Nik is one day
Thus, 17/40 work is done by Mike and Nik in = (360/17) * (17/40) = 9 days
Hence Option C is the correct one.

Example 10: Ross and Sam can finish an assignment in 15 days together. Ross can complete this Assignment alone in 20 days. Calculate the days taken by Sam to do the same assignment alone?
(a) 25
(b) 60
(c) 30
(d) 33
Ans: (b)
Ross and Sam’s one day’s effort =1/15
Ross’s one day’s effort =1/20
Therefore, Sam’s one day’s effort = (Ross and Sam)’s one day’s effort- Ross’s one day’s effort
=1/15 - 1/20 = 1/60
Hence, Sam can finish the Assignment in 60 days
Therefore option B is the correct one.