Practice Questions: Geometry - SSC CGL PDF Download
Definition
At its most basic level, geometry is the mathematical exploration of shapes and space. It encompasses the study of flat, two-dimensional shapes like squares and circles, as well as three-dimensional shapes with depth, such as cubes and spheres.
Concept
Before delving into two-dimensional and three-dimensional shapes, it's crucial to understand the fundamental geometric elements that contribute to these shapes: points, lines, line segments, rays, and planes.
- A point is symbolized by a dot, denoting a specific location in space.
- A line comprises straight points that extend infinitely in both directions, marked by arrows on either end.
- Rays are lines with one endpoint, while line segments have endpoints on both sides. Planes are surfaces that extend infinitely in all directions.
The concept of geometry revolves around two types of shapes: 3D and 2D shapes. Let's briefly explore them:
- Two-dimensional objects possess only two dimensions: length and width.
- In contrast, three-dimensional objects have a third dimension, depth, making them not flat. Examples of three-dimensional objects include cubes, spheres, and pyramids. A cube, for instance, consists of six square sides.
Q1: If angles P and Q are complementary to one another, and angle P is two times of angle Q. Calculate the measures of angles P and Q.
(a) 60°
(b) 90°
(c) 120°
(d) None
Ans: (a)
Let the measure of angle P be P, and the measure of angle Q be Q.
P = 2Q
Given that angles P and Q are complementary. Therefore,
P + Q = 90°
But, P = 2Q. Therefore,
2Q + Q = 90
3Q = 90
Q= 90/3 = 30°
P =2Q = 60°
Q2: The given triangle ABC is a right triangle. Angle ABC is 600. Find the measure of triangle APC.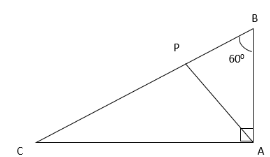 (a) 56°
(a) 56°
(b) 40°
(c) 75°
(d) 80°
Ans: (c)
The sum of all the angles in the given triangle ABC is 180°
180 = 60 + 90 + BCA
Therefore, angle BCA = 180-150= 30°
Angle APC = 60 + 45- 180
180-105 = 75°
Q3: What is the measure of angle A in the given figure?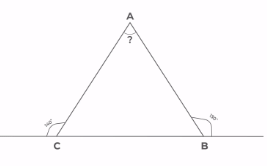 (a) 66°
(a) 66°
(b) 90°
(c) 85°
(d) 30°
Ans: (b)
The internal angle B in the given triangle = 180-130 = 50°
The internal angle C in the given triangle = 180-140 = 40°
Therefore, in the given triangle, measure of angle A = 180 – (40 + 50)
180 – 90 = 90°
Q4: In the given figure, determine the value of angle RPB.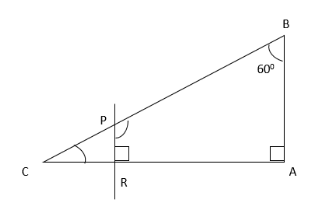 (a) 60°
(a) 60°
(b) 120°
(c) 80°
(d) 70°
Ans: (b)
In the given triangle ABC, value of angle C = 180 – (60+90)
180 – 150 = 30°
Now, in the given triangle PCR, value of angle R = 900
Value of angle CPR = 180 – (90+30)
180 – 120 = 60°
Now, value of angle RPB = (180 - 60) = 120°
Q5: What will be the area of the presented figure when all its sides are given?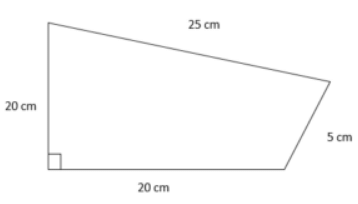 (a) 11 cm²
(a) 11 cm²
(b) 13 cm²
(c) 10.72 cm²
(d) None of the above
Ans: (c)
The presented figure can be divided into two triangles to calculate the area.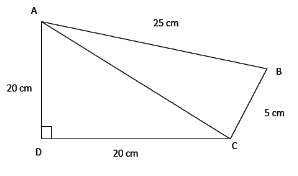 We can also label the given figure to identify and mark the 2 triangles.
We can also label the given figure to identify and mark the 2 triangles.
Now the figure consists of triangles: ADC and triangle ACB.
The area of the given triangle can be calculated when we know the measure of length AC.
For this, in the given triangle, ADC,
AC2 = AD2 + DC2
AC2 = 202 + 202
AC =√400+400
AC = √800
AC = 28.28
Area of triangle ADC = ½*20*20
= 200 cm²
We also need the area of the triangle ABC
Area of the triangle when its three sides are given = √p(p-a)(p-b)(p-c)
Where p = (a+b+c)/2
P = (25+5+28.28)/2 = 29.14
Therefore, area of triangle = √29.14(29.14-25)(29.14-5)(29.14-28.28)
= √115.08
= 10.72 cm²
Q6: What is the value of angle A in the given figure?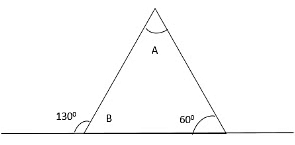 (a) 30°
(a) 30°
(b) 70°
(c) 80°
(d) 90°
Ans: (b)
To calculate the measure of angle A, we have to calculate the value of angle B.
Angle B = 180-130= 50°
Therefore, the measure of angle A = 180 – (50+60)
A = 180-110
A =70°
Q7: In the given figure, angle CEB = 1200. Calculate the measure of angle AED.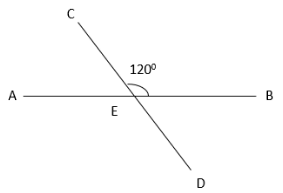 (a) 56°
(a) 56°
(b) 40°
(c) 120°
(d) 80°
Ans: (c)
From the given figure, angle DEB = 180-120 = 60°
Therefore, angle AED = 180-60 = 120°
Q8: Calculate the value of angle EDB when the remaining angles are given. (a) 50°
(a) 50°
(b) 40°
(c) 75°
(d) 90°
Ans: (a)
In the given triangle ACE, vale of angle AEC = 180- (60+40)
= 180 – 100
= 800
Also, the given angle DEB = 800 as it is directly opposite to angle AEC.
= In triangle DEB, value of angle EDB = 180 – (80+50)
=180 – 130
50°
Q9: Calculate the area enclosed by ABDEF.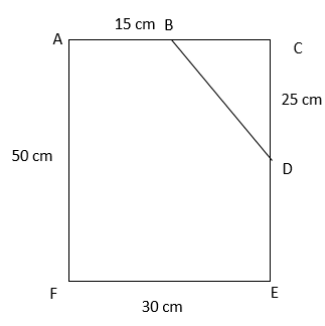
(a) 1312.5 cm2
(b) 200 cm2
(c) 350 cm2
(d) None of the above
Ans: (a)
Area of ABDEF = area of ACEF – area of triangle BCD
= 50 x 30 – ((1/2)*15*25)
= 50 x 30 – 187.5
= 1500 – 187.5
= 1312.5 cm2
Q10: Determine the area of the given triangle.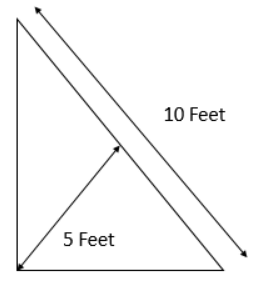 (a) 25cm²
(a) 25cm²
(b) 15cm²
(c) 10 cm²
(d) 55cm²
Ans: (a)
The solution is to rotate the triangle to bring the 10 feet side at the bottom.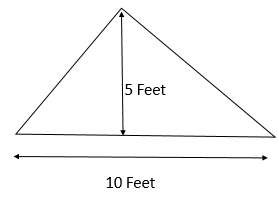 Therefore, the area of the triangle = Area = 25cm²
Therefore, the area of the triangle = Area = 25cm²
FAQs on Practice Questions: Geometry - SSC CGL
| 1. What is the definition of geometry? |  |
| 2. What are some common geometric shapes? |  |
| 3. How is geometry used in everyday life? |  |
| 4. What are the different types of angles in geometry? |  |
| 5. What is the Pythagorean theorem in geometry? |  |


















