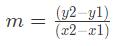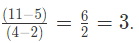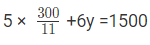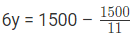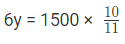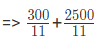Tips and Tricks: Linear Equations | Quantitative Aptitude for SSC CGL PDF Download

Definition of Linear Equation

A linear equation is a mathematical expression that corresponds to a straight line within a two-dimensional Cartesian coordinate system. It takes the form y=mx+b, where x and y represent variables, m denotes the slope of the line, and b signifies the y-intercept.

Linear Equation Tips and Tricks and Shortcuts

• In this guide, we present swift and straightforward tips and tricks for tackling Linear Equation questions efficiently in competitive exams and various recruitment assessments, aiming to enhance your performance.
• Eliminating incorrect options is a practical approach to solve these problems. This involves substituting the provided values into the equation and identifying the option that satisfies it.
• Linear equations typically follow the standard form y= mx+b. Exams often feature two types of questions related to this form, as explained below.

Shortcuts for solving Linear Equation

There are several shortcuts and techniques to solve linear equations quickly and efficiently. Here are some useful shortcuts:

• Combine Similar Terms: Prior to solving, simplify the equation by combining like terms on both sides.
• Isolate the Variable: Work towards placing the variable (typically x) on one side of the equation by employing inverse operations (addition, subtraction, multiplication, division) to move all other terms to the opposite side.
• Utilize Fractional Form: When the equation involves fractions, working with the equation in fractional form is often more manageable, helping to avoid dealing with large numbers.
• Cancellation: If there are terms with the same factor on both sides of the equation, you can cancel them out to streamline the equation.
• Multiply to Eliminate Fractions: To remove fractions, multiply the entire equation by the least common multiple (LCM) of the denominators.
• Cross-Multiplication: In equations involving proportions or fractions, employ cross-multiplication as a method to simplify and solve for the variable.

Employing these quick methods and strategies not only saves time but also enhances your proficiency in solving linear equations. Nevertheless, it's crucial to retain an understanding of the principles behind each shortcut to maintain accuracy in your solutions.

Type 1: Linear Equations Shortcuts. To Find the value of x or y.

Example 1: If 3a + 6 = 4a − 2, then find the value of a?
(a) 3
(b) 8
(c) 6
(d) 7
Ans: (b)
We can use the trick of eliminating the option
Option 1, put a = 3
3 * 3 + 6 = 15
4 * 3 -2 = 10
This means option 1 is incorrect.
Now, check for option 2, put a = 8
3 * 8 + 6 = 30
4 * 8 – 2 = 30
This means option 2 satisfies the equation. Therefore, it is the correct option.

Example 2: Which of the following is the correct equation of the line passing through the points (2, 5) and (4, 11)?
(a) y = 3x + 1
(b) y = 2x + 1
(c) y = 2x + 3
(d) y = 3x + 5
Ans: (a)
To find the equation of a line passing through two given points, we first calculate the slope (m) using the formula:

For the points (2, 5) and (4, 11), the slope is
Next, we use the point-slope form of the linear equation:
y – y₁ = m(x – x₁)
Plugging in the values (2, 5) and m = 3, we get the equation y – 5 = 3(x – 2). Solving for y, we find y = 3x + 1.

Type 2: Tips And Tricks for Linear Questions Word problems

Example 1: The cost of 5 blankets and 6 bedsheets is Rs.1500. The cost of 6 blankets and 5 bedsheets is Rs.1300. Find out the total cost of one blanket and one bedsheet.
(a) Rs. 255
(b) Rs. 250
(c) Rs. 81.81
(d) Rs. 254.545
Ans: (d)
Let the cost of blankets be x and the cost of bedsheets be y.
According to the question:
5x+ 6y= 1500…(1)
6x+ 5y=1300…(2)
Multiply Eq 1 by 5 and Eq 2 by 6,
we get.
25x+30y = 7500…(3)
36x+30y = 7800…(4)
Subtract equation (3) from equation (4)
11x = 300
x = 300/11




 y = 2500/11
Total cost = x+y

 = 2800/11 = 254.545

Example 2: What is the x-intercept of the line represented by the equation 2x + 3y = 12?
(a) 4
(b) 6
(c) 8
(d) 12
Ans: (b)
To find the x-intercept, we set y = 0 and solve for x.
Substituting y = 0 into the equation 2x + 3y = 12, we get 2x + 3(0) = 12. Simplifying, we find 2x = 12, and then x = 6.

Example 3: If the line 3x – y = 5 is parallel to the line 2x + ky = 8, what is the value of k?
(a) -3
(b) -2
(c) 2
(d) 3
Ans: (b)
 Two lines are parallel if their slopes are equal.
The slope of the line 3x – y = 5 can be found by rearranging the equation in slope-intercept form (y = mx + b), where m is the slope.
So, 3x – y = 5 becomes y = 3x – 5, and the slope is 3.
The line 2x + ky = 8 can also be rearranged as y = -(2/k)x + 8/k, where the slope is -2/k. To make both slopes equal (3 and -2/k), we need -2/k = 3. Solving for k, we find k = -2/3.