Solved Examples: Quadratic Equations | Quantitative Aptitude for SSC CGL PDF Download
Definition of Quadratic Equation
A quadratic equation takes the form ax2 + bx + c = 0, representing a second-degree polynomial equation, where 'a', 'b', and 'c' are constants, and 'x' is the variable. It is essential for 'a' to be nonzero to validate it as a genuine quadratic equation.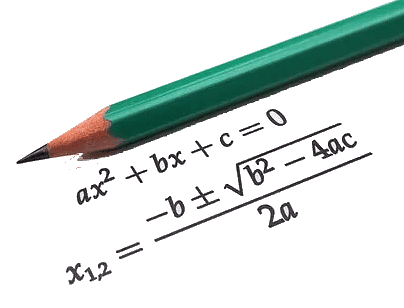
Methods for finding roots of Quadratic Equation
The roots or solutions of a quadratic equation are the values of ‘x’ that satisfy the equation, making it true. A quadratic equation can have two real roots, two complex roots, or one real root (in case of a perfect square). The number of roots is determined by the value of the discriminant (Δ) given by:
Δ = b2 −4ac
- If Δ > 0, the quadratic equation has two distinct real roots.
- If Δ = 0, the quadratic equation has one real root (repeated or equal roots).
- If Δ < 0, the quadratic equation has two complex roots (conjugate pairs).
To find the roots of a quadratic equation, several methods can be used:
- Factoring: If the equation can be factored, the roots can be directly determined from the factors.
- Quadratic Formula: The quadratic formula is a general method to find the roots of any quadratic equation and is given by:
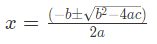 where the ± sign accounts for the two possible solutions.
where the ± sign accounts for the two possible solutions. - Completing the Square: This method involves transforming the quadratic equation into a perfect square form, from which the roots can be easily obtained.
Rules for Quadratic Equations
- If p+ √q is a root of a quadratic equation, then its other root is p-√q.
- When D ≥ 0, then rx2+ dx + z can be expressed as a product of two linear factors.
- If α and β are the roots of rx2+ dx + z, then we can write it as: x2 – (α + β)x + α β = 0.
Examples
Example1: If x2 - 3x + 1 = 0, find the value of x + 1/x,
(a) 0
(b) 3
(c) 2
(d) 1
Ans: (b)
Given equation is
x2 - 3x + 1 = 0 ⇒ x2 + 1 = 3x
⇒ x2 + 1/x = 3
⇒ x2/x + 1/x = 3
∴ x + 1/x = 3
Example 2: For what value of k, the equation x2 + 2(k - 4) x + 2k = 0 has equal roots ?
(a) 6 and 4
(b) 8 and 2
(c) 10 and 4
(d) 12 and 2
Ans: (b)
Given equation is
x2 + 2(k - 4)x + 2k = 0
On comparing with ax2 + bx + c = 0
Here, a = 1, b = 2(k -4), c = 2k
Since, the root are equal, we have D = 0.
b2 - 4ac = 0
∴ 4(k - 4)2 - 8k = 0
4(k2 + 16 - 8k) - 8k = 0
⇒ 4k2 + 64 - 32k - 8k = 0
⇒ 4k2 - 40k + 64 = 0
⇒ k2 - 10k + 16 = 0
⇒ k2 - 8k - 2k + 16 = 0
⇒ k(k - 8) -2 (k - 8) = 0
⇒ (k - 8) (k - 2) = 0
Hence, the value of k 8 or 2.
Example 3: If α and β are the roots of the equation 4x2 - 19x + 12 = 0, find the equation having the roots 1/α and 1/β
(a) 4x2 + 19 + 12 = 0
(b) 12x2 - 19x + 4 = 0
(c) 12x2 + 19x + 4 = 0
(d) 4x2 + 19x - 12 = 0
Ans: (b)
Given equation is 4x2 - 19x + 12 = 0
Let given equation having the roots 1/α and 1/β,
Then required equuation is
12x2 - 19x + 4 = 0
Example 4: If one of the roots of quadratic equation 7y2 - 50y + k = 0 is 7, then what is the value of k ?
(a) 7
(b) 1
(c) 50/7
(d) 7/50
Ans: (a)
Given quadratic equation is
7y2 - 50y + k = 0
If one root is 7, then it will satisfy the equation i.e putting y = 7 in equation
7 x (7)2 - 50 x 7 + k = 0
⇒ 7 x 49 - 350 + k = 0
⇒ 343 - 350 + k = 0
∴ k = 7
Example 5: The quadrictic equation whose roots are 3 and -1, is
(a) x2 - 4x + 3 = 0
(b) x2 - 2x - 3 = 0
(c) x2 + 2x - 3 = 0
(d) x2 + 4x + 3 = 0
Ans: (b)
Given that, the roots of the quadrictic equation are 3 and -1.
Let α = 3 and β = -1
Sum of roots = α + β = 3 - 1 = 2
Products of roots = α . β = (3) (-1) = -3
∴ Required quadric equation is
x2 - (α + β)x + α β = 0
⇒ x2 - (2)x + (-3) = 0
⇒ x2 - 2x - 3 = 0
|
315 videos|182 docs|185 tests
|
FAQs on Solved Examples: Quadratic Equations - Quantitative Aptitude for SSC CGL
| 1. What is a quadratic equation? |  |
| 2. How do you solve a quadratic equation by factoring? |  |
| 3. Can a quadratic equation have more than two solutions? |  |
| 4. What is the quadratic formula and how is it used to solve quadratic equations? |  |
| 5. Are there any real-life applications of quadratic equations? |  |
















