Types of Games and Tournaments | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Introduction
- Games and tournament-based reasoning scenarios have become a prevalent element in aptitude exams, particularly in management entrance tests such as CAT, XAT, and other prominent examinations.
- Solving these questions requires a clear understanding of the situations given. It helps to know common strategies used to solve different types of problems in the games and tournaments chapter.
Analysis Tools for a Tennis/Badminton or a Knockout Tournament
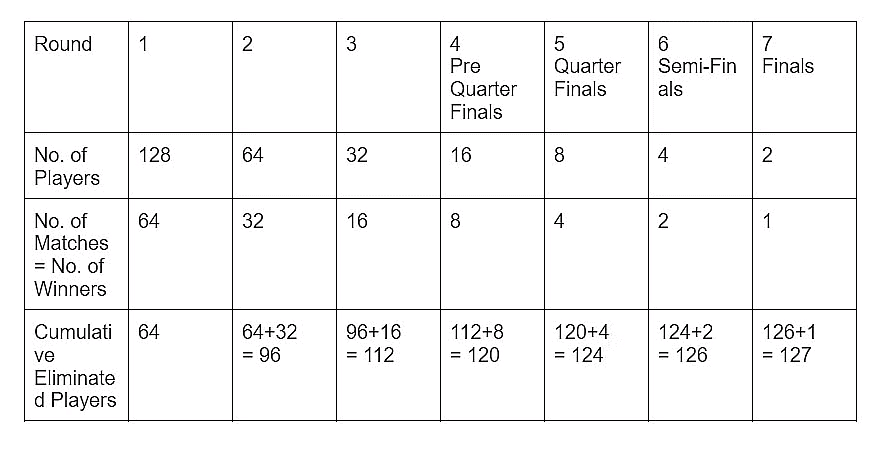
(i) The tournament, as indicated in the table, encompasses a total of 127 matches, calculated as the sum of 64 + 32 + 16 + 8 + 4 + 2 + 1.
(ii) Each round results in the elimination of half the remaining players, with the other half, the winners, advancing to the subsequent round. (iii) The ultimate victor in the tournament is determined after the completion of the 127th match.
(iii) The ultimate victor in the tournament is determined after the completion of the 127th match.
Consider a 64-player tournament, which spans 6 rounds and requires 63 matches to determine the winner. Similarly, a 32-player tournament involves 5 rounds and 31 matches for a conclusive outcome.
An interesting aspect is the introduction of byes in tournaments when the number of players in any round is not even. Take, for instance, a tournament with 121 players, where the structure unfolds as follows:
- Round 1: 60 matches and 1 bye – a total of 61 players progress to the second round.
- Round 2: 30 matches and 1 bye – resulting in 31 players advancing to the third round.
- Round 3: 15 matches and 1 bye – leading to a total of 16 players progressing to the fourth round.
Subsequently, the tournament proceeds without further byes.
To calculate the total number of matches in such a tournament,
- The count is determined as follows: 60 + 30 + 15 + 8 + 4 + 2 + 1 = 120 (one less than the number of players.)
- In general, the total number of matches in a knockout tournament of n players = (n - 1).
- This can be understood as needing to identify 122 losers to determine the winner in a 123-player tournament, and since each match determines one loser, 122 matches are required.
- For a knockout tournament with 13 players, a total of 12 matches will play. It is recommended to construct tournament structures for various player counts and explore the rounds required for each tournament.
- Another noteworthy observation concerns the number of rounds. For a 128-player tournament, it necessitates 7 rounds, while a 64-player tournament requires 6 rounds, and a 32-player tournament requires 5 rounds. This pattern continues, and if we examine a 65-player tournament:
- Round 1: 32 matches and 1 bye – 33 players progress to round 2.
- Round 2: 16 matches and 1 bye – resulting in 17 players advancing to round 3.
- Round 3: 8 matches and 1 bye – leading to 9 players progressing to round 4.
- Round 4: 4 matches and 1 bye – 5 players progress to round 5.
- Round 5: 2 matches and 1 bye – 3 players advance to round 6.
- Round 6: 1 match and 1 bye – 2 players move on to round 7.
- Round 7: 1 match – deciding the tournament winner.
Thus, a crucial logic emerges regarding the number of rounds: for tournaments with 65 to 128 players, the number of rounds is always 7. For 33 to 64 players, 6 rounds are required, and so forth, following a pattern related to powers of 2.
Seeding And Logic Around Seeding
In knockout tournaments such as tennis and badminton, top players are often assigned seedings based on their anticipated chances of winning.
Seed number 1 is commonly known as the top seed, and tournament draws are structured according to these seedings.
For instance, in a 32-player tournament, the initial round comprises 16 matches, with matchups determined by the assigned seed numbers. The subsequent points highlight key aspects of this seeding system: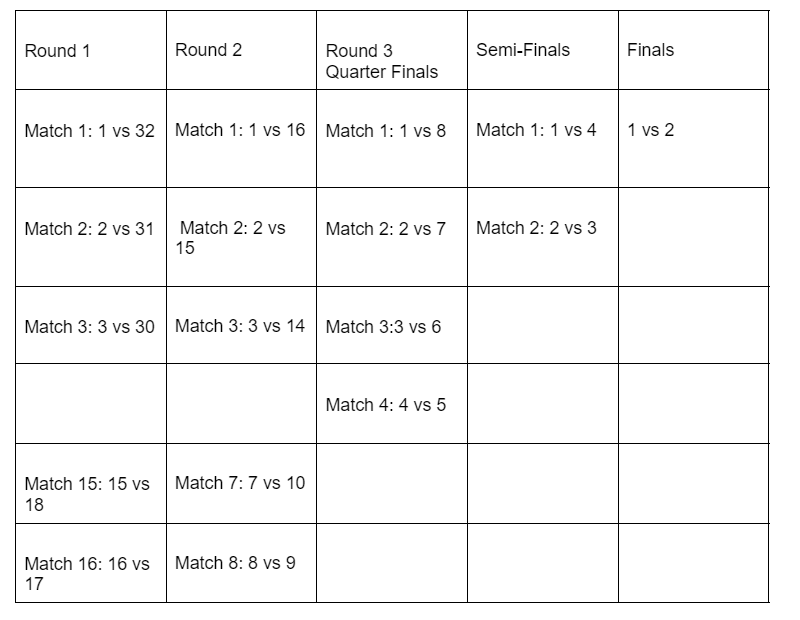
- Higher Seed vs. Lower Seed Matches: Every match features a higher seed playing against a lower seed. The expectation is that the higher seed will emerge victorious and progress to the next round. Subsequent round pairings are based on the assumption that the higher seed wins.
- Potential Upsets: The smooth progression of matchups can be disrupted in the event of an upset, where a lower seed defeats the higher seed. This unexpected outcome is termed an upset and can lead to different matchups than initially anticipated.
- Variability in Match Pairings: Visualizing the scenarios, consider match 1 of round 2. The expected matchup is seed 1 vs. seed 16. However, potential upsets in round 1 could result in alternative pairings such as 1 vs. 17, 32 vs. 16, or 32 vs. 17, depending on the winners of the first-round matches involving seeds 1 and 16.
- Multiple Possibilities in Subsequent Rounds: Extending this variability to match 1 of round 3, winners from matches 1 and 8 of round 2 influence the potential matchups. With various outcomes in match 1 of round 2, involving players like 1, 16, 17, or 32, and similar variability in match 8 of round 1, there can be 16 different possible matchups for match 1 of round 3.
Solved Examples: Knockout Tournament
Direction for Questions 1 to 4:In the following table is the listing of players, seeded from the highest (#1) to the lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round, quarterfinals and semi-finals. In the first round, the highest seeded player plays the low-est seeded player (seed #32) which is designated match no. 1 of the first round; the 2nd seeded player plays the 31" seeded player which is designated match no. 2 of the first round and so on. Thus, for instance, match no. 16 of the first round is to be played between 16" seeded player and the 17 seeded player. In the second round, the winner of match no. 1 of the first round plays the winner of match no. 16 of first round and is designated match no. 1 of the second round. Similarly, the winner of match no. 2 of first round plays the winner of match no. 15 of the first round and is designated match no. 2 of the second round. Thus, for instance, match no. 8 of the second round is to be played between the winner of match no. 8 of the first round and the winner of match no. 9 of the first round. The same pattern is followed for later rounds as well.
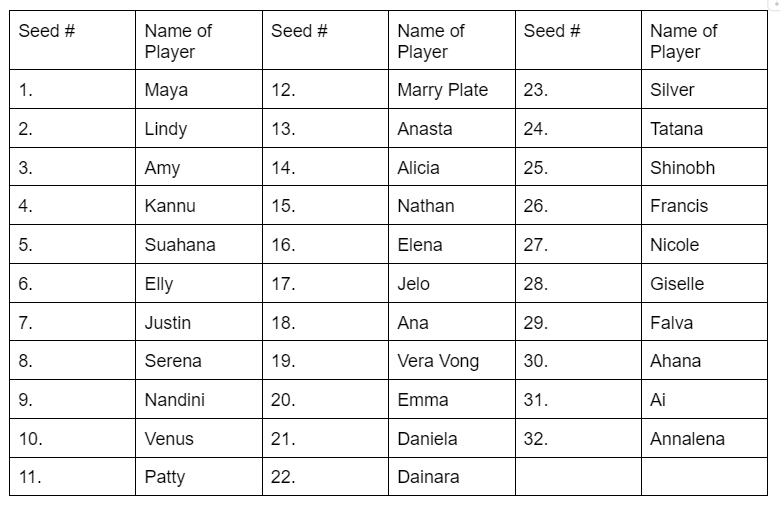
Que 1: If Elly and Serena lose in the second round, while Justin and Nandini make it to the semi-finals, then who would play Maya in the quarterfinals, in the event Maya reaches quarterfinals?
(a) Dainara
(b) Justin
(c) Nandini
(d) Patty
Que 2: If the top eight seeds make it to the quarterfinals, then who, amongst the players listed below would definitely not play against Maya in the final, in case Maya reaches the final?
(a) Amy
(b) Elly
(c) Kannu
(d) Lindy
Que 3: If there are no upsets a lower seeded player beating a higher seeded player) in the first round, and only match numbers 6, 7 and 8 of the second round result in upsets, then who would meet Lindy in quarterfinals, in case Lindy reaches quarter finals?
(a) Justin
(b) Nandini
(c) Patty
(d) Venus
Que 4: If, in the first round, all even numbered matches (and none of the odd numbered ones) result in upsets, and there are no upsets in the second round, then who could be the lowest seeded player facing Maya in semi-finals?
(a) Anasta
(b) Falva
(c) Nandini
(d) Suahana
Solution: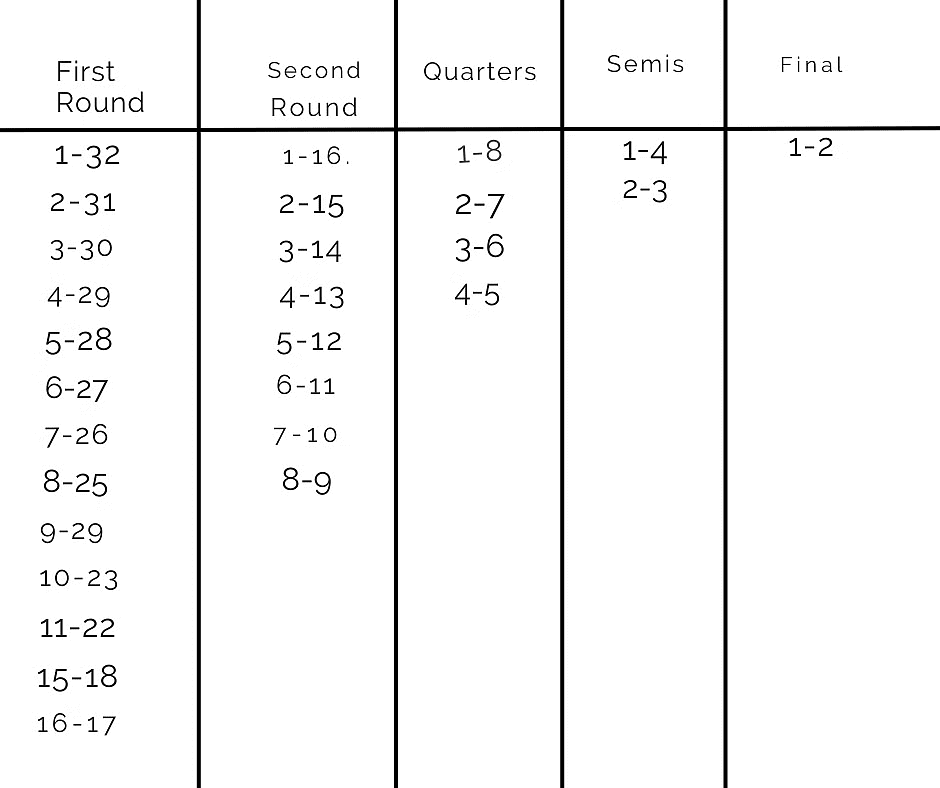
Sol 1: Option (c) is correct.
Explanation : In the quarters, Maya is seeded to play the 8th seed (Serena ). But Serena loses in the second round (where she must have played either the 9th or the 24th seed). But, it can be seen that the 9th seed Nandini reaches the semis.
Hence, Maya must play Nandini in the quarterfinals.Sol 2: Option(c) is correct.
Explanation : Maya is seeded to meet the 8th seed in the quarters and the 4th/5th seed in the semis. Neither of them can play her in the final, since they have to meet in the earlier rounds. Amongst these, only Kannu' name figures in the options.Sol 3: Option (d) is correct.
Explanation : Lindy being the 2d seed is scheduled to play the winner of the match 7 of the second round in the quarters. As per the question, match 7 has resulted in an upset in the second round. This means that Venus won the match 7 and will play Lindy in the quarters.Sol 4: Option (a) is correct.
Explanation: According to this question, seeds 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29 and 31 will reach the second round. In such a case, 4" seed is replaced by 29" seed. In the second round Seed 29 will play seed 13 and 13 will win, because there is no upset in the second round. In the third round the winner of 5 and 13 play each other. The result of round 3 is not known. Hence, the lowest seeded player who could play Maya in the Semis would be seed 13 - Anasta.
Analysis Tools for a Hockey/Football Tournament (Round Robin)
Hockey and football tournaments organized in a round-robin format offer intriguing scenarios for constructing reasoning questions. After two rounds of a round-robin tournament, the standings table may display results such as A vs F 5-0, A vs E 6-2, B vs C 2-1, B vs D 1-1, C vs D 4-1, and E vs F 0-0. A typical table reflecting these results could look like this:
Note: Wins are awarded 3 points, and draws earn 1 point.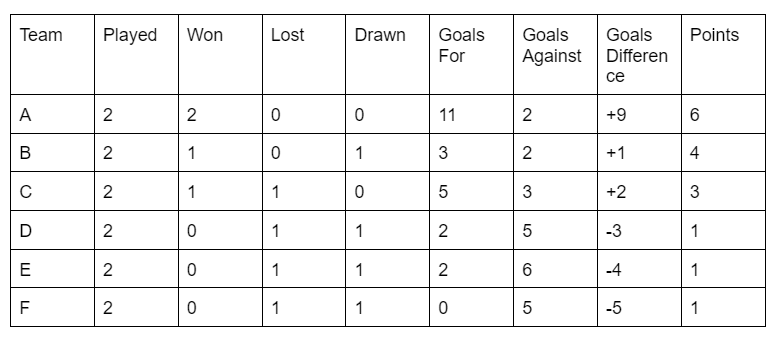 In scenarios where individual match results are omitted, deductions can be made based on certain observations and rules that consistently apply:
In scenarios where individual match results are omitted, deductions can be made based on certain observations and rules that consistently apply:
- Total Matches Played: The total number of matches played equals half of the total matches in the "Played" column. Each match contributes +1 to the "Played" column for both teams involved. In this table, the sum of matches played is 12, indicating 6 matches have taken place in the tournament.
- Number of Wins: The number of wins is equivalent to the number of losses in the "Losses" column. This balance results from the increment of +1 in both columns for each decisive match.
- Number of Decisive Matches: The number of decisive matches equals the sum in either the "Wins" or the "Losses" column. In this case, with a total of 4 wins, it indicates that 4 out of the 6 matches played were decisive.
- Number of Draws: The number of drawn matches is derived by dividing the sum of the "Drawn" column by 2. In this example, the number of drawn matches is 4/2 = 2.
- Goals For - Goals Against = Goal Difference: The "Goals For" column represents goals scored by the team, and the "Goals Against" column indicates goals scored against the team. The sum of the "Goal Difference" column is always zero.
- Sum of Goals For Column = Sum of Goals Against Column: This equality holds because every goal scored results in an increment of +1 in both the "Goals For" and "Goals Against" columns.
Additionally, specific deductions can be made based on score patterns, such as a team winning both matches with a goals for of 2 and goals against of 0 indicating 1-0 victories.
These observations and rules provide a systematic approach to deducing match results from standings tables in round-robin tournaments. Further examples and regular exposure to such scenarios will enhance the ability to interpret and analyze similar tables effectively.
Solved Example: Round Robin
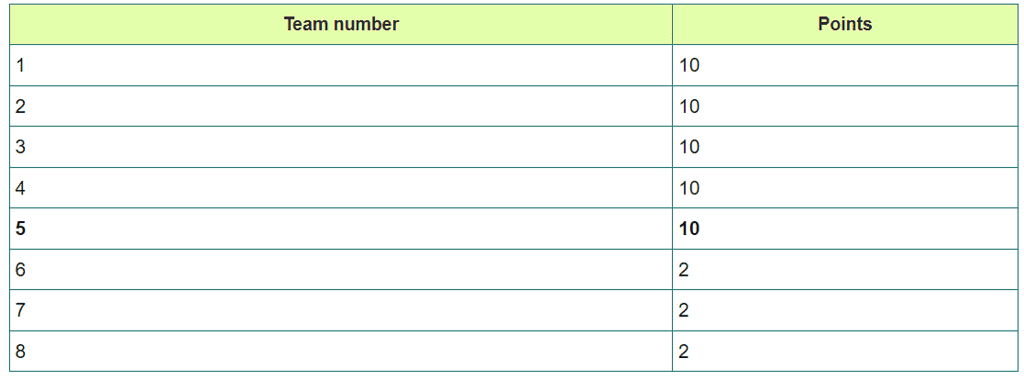
Example: There are 16 teams and they are divided into 2 groups of 8 each. Each team in a group plays against one another on a round-robin basis. Two points are awarded for a win, one point for a tie and zero for a loss. The top four teams from each group will qualify for the next round i.e. round 2. In Round 2, each team of one group will play with each team of group two. At the end of the second round, the top four teams in terms of the points scored advance to the semi finals and the winners of the semi finals play the finals. In case of teams having the same number of wins, the team with better run-rate would be ranked ahead.
Total 16 teams
Two group - Each group having 8 teams.
Points - Win: 2, Tie / Draw: 1, Loss: 0
Top four from each group will go to the next round.
(4 Matches)Semi Finals (2 Matches), Final.
i) What is the total number of matches played in the tournament?
a) 50
b) 56
c) 28
d) 75
Sol: Option 'd' is correct.
Explanation:
Total matches = Number of group A matches + Number of group B matches + Round 2 + Semi-Finals + Final
= 82 + 8C2 + 4C1 x 4C1 + 2 + 1
= 28 + 28 + 16 + 2 + 1 = 75 matches
ii) What is the least number of points with which a team can advance to the round 2?
a) 5
b) 4
c) 10
d) 8
Sol: Option 'b' is correct.
Explanation: As we have seen in key points that if we are looking for minimum points then we will have to go from Top to Bottom.
In given question we have to find out "Least number of points" which means minimum number of points. SO we will have to start point distribution from Top to Bottom.
Now, let assume that top #1 team won all its 7 matches. (14 Points)
Top #2 team won all its matches except against #1 team. (12 Points)
Top #3 team won all its matches except against #1 and #2 matches. (10 Points)
Now we are left with 20 points (i.e. Total points for group one matches 56 - (14 + 12 + 10) = 20).
Now remaining 5 teams have lost 3 matches with top teams. So, they are left with 4 matches with others. We will distribute remaining points equally to them i.e. 20 / 5 = 4.
So, remaining 5 teams will now have 4 - 4 points and here run rate checking scenario occurs.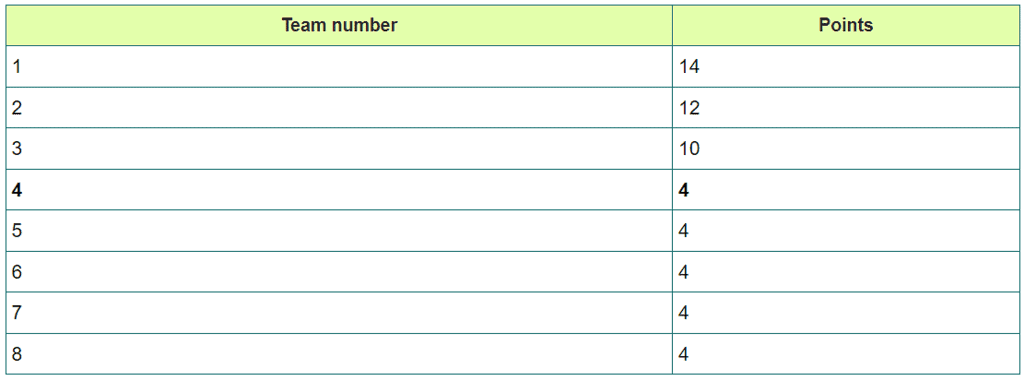
So, minimum or least 4 Points are required for getting into second round.
iii) What is the maximum possible number of points that can be scored by a team that is eliminated at the firstround?
a) 14
b) 12
c) 10
d) 8
Sol: Option 'c' is correct.
Explanation: In this case we have to find out maximum possible number of points that can be scored by a team which is eliminated after first round (Simply, by Low run rate)
As we have mentioned in key points that for finding maximum points we have to start from bottom to top.
We will make a group of Bottom 3 teams and another of Top 5 teams.
Let’s assume that bottom 3 team will lose their matches against top teams. So, they will have total 3 matches left for winning. (Those 3 teams will play against each other) Total 6 points they can have. We will distribute those points equally between them. i.e. 2 points for each team.
Now, we have to give top 5 teams equal points. So that we can have top 4 team in next round and team #5 is eliminated after first round though it can have maximum number of points.
So, remaining 50 points (i.e. Total points 56 - 6 Points distributed amongst bottom 3 teams = 50 Points) will be distributed equally amongst 5 team that is 10.
Now, team #5 will also have 10 Points but it will be out of the league because of low run rate. So, answer is 10.
Analysis Tools for a Cricket Scorecard
- In cricket, a batting scorecard typically presents the names of players alongside their individual runs scored and the overall team score.
- At any point during an innings, there are two batsmen at the crease, forming a partnership. Each such pair is denoted as a partnership, and the runs scored while they bat together contribute to that specific partnership.

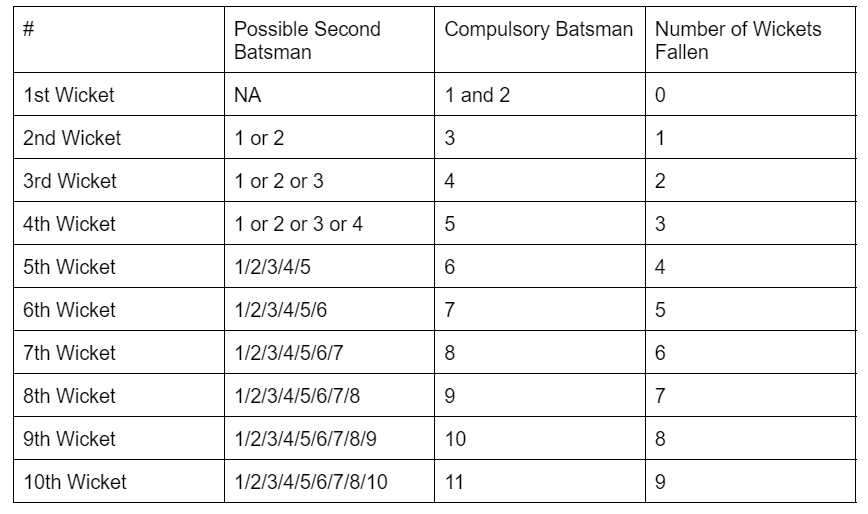
- The batsmen are numbered from 1 to 11, with batsman 1 taking the first strike during an innings. The accompanying batsman is referred to as batsman 2. The sequence continues until batsman 11, the last batsman to come in during an innings.
- The first partnership is between the two opening batsmen. Once one of them gets out, the incoming batsman is numbered as batsman 3 and joins the not-out batsman to form the second wicket partnership.
- Subsequent partnerships follow this pattern, with the incoming batsman taking the next available number. For instance, the third wicket partnership involves three possibilities: batsman 1 and batsman 4, batsman 2 and batsman 4, and batsman 3 and batsman 4.
- The trend continues until the 10th wicket partnership, which is the last partnership of the innings.
- Each partnership has specific batsmen, such as batsman 4, who is a constant in the third wicket partnership. The remaining batsman, whether numbered 1, 2, or 3, depends on who got out and who remains not out.
- The table of possible partnerships can be visualized with batsman numbers and the corresponding partnerships, illustrating the combinations possible for each wicket partnership.
- The innings concluded with the fall of the 10th wicket, marking the termination of the batting team's turn to bat.
- Specific batsmen can be identified to be batting at the fall of a particular wicket. For example, if batsman number 1 scores 100 runs and the first four wickets fall at 22, 38, 47, and 73 runs, then batsman 1 is part of the fifth wicket partnership, in addition to the earlier wicket partnerships.
- A batsman's strike rate is calculated as the number of runs scored per 100 balls faced. For instance, if a batsman has a strike rate of 50 and faces 40 balls before getting out, it implies the batsman scored 20 runs.
- Run rate is defined as the number of runs scored per over. In a 50-over match, a team scoring at 5 runs per over would accumulate a total of 250 runs if they play all 50 overs.
- The bowling scorecard provides information on the bowlers' performance for the bowling side. Key details include the number of overs bowled, maidens (overs with no runs scored), runs conceded, and wickets taken by each bowler.
- Extras refer to runs given to the batting team that were not scored by the batsmen off their own bat. Extras include wides, no balls, byes, and leg byes. These runs contribute to the team's total score, indicating that the overall innings total is the sum of runs scored by the batsmen and the runs in extras awarded to the team.
Round Robin Tournament or Round Robin Cum Knock out Tournament
In a Round-Robin Tournament involving n teams, where each team competes against every other team exactly once, the total number of matches in the tournament can be determined using the combination formula: nC2

For instance, in a round-robin tournament with 6 teams, applying the combination formula (6C2) reveals that there would be a total of 15 matches. [Note: The formula for combinations is used, where nC₂ represents the number of ways to choose 2 items from a set of n items.]
The general application of the combination formula allows for the calculation of the total number of matches in a round-robin tournament with any given number of teams, providing a systematic approach to understanding the tournament structure.
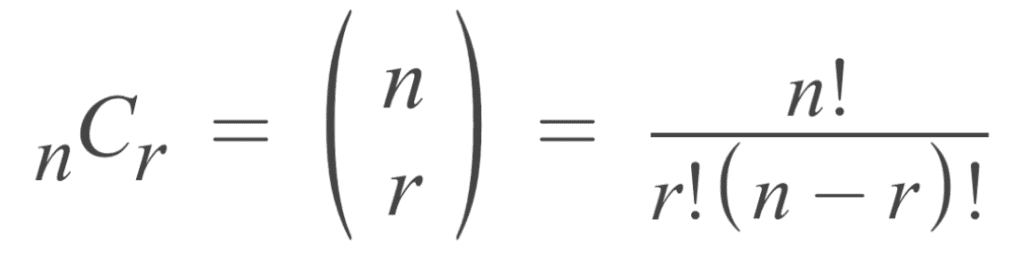 1. Tournaments are often structured as a combination of round-robin and knockout formats, creating a round-robin cum knockout tournament.
1. Tournaments are often structured as a combination of round-robin and knockout formats, creating a round-robin cum knockout tournament.
2. In the initial rounds, teams are divided into multiple groups, and each group operates on a round-robin basis. Within a group, teams face each other once, and based on their performance, the top teams advance to the next stage.
3. The knockout phase follows the round-robin stage and typically begins with either the semi-final, quarter-final or pre-quarterfinal, depending on the tournament's structure.
4. The FIFA World Cup in football serves as a classic example of this format. The tournament starts with 8 groups, each consisting of 4 teams. Teams within a group engage in round-robin matches, and the top two teams from each group progress to the next stage.
5. The subsequent round, whether it be pre-quarterfinals, quarterfinals, or semi-finals, adopts a knockout format, adding an extra layer of intensity and competition to the tournament.
Solved Examples
Instructions: Answer the following questions based on the information given below
Example 1: In a sports event, six teams (A, B, C, D, E and F) are competing against each other Matches are scheduled in two stages. Each team plays three matches in Stage – I and two matches in Stage – II. No team plays against the same team more than once in the event. No ties are permitted in any of the matches. The observations after the completion of Stage – I and Stage – II are as given below.
Stage-I:
• One team won all the three matches.
• Two teams lost all the matches.
• D lost to A but won against C and F.
• E lost to B but won against C and F.
• B lost at least one match.
• F did not play against the top team of Stage-I.
Stage-II:
• The leader of Stage-I lost the next two matches
• Of the two teams at the bottom after Stage-I, one team won both matches, while the other lost both matches.
• One more team lost both matches in Stage-II.
Question 1: The two teams that defeated the leader of Stage-I are:
a. B & F
b. E & F
c. B & D
d. E & D
Sol: Option 'b' is correct.
Explanation: There are a total of 6C2 matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.
From the information given, we can conclude that the following matches were held in first stage:
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)
One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.
From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).
Thus, the stage 1 matches are
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)
Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)
As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:
Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)
Hence, the two teams that won against stage 1 leader A are E and F.
Question 2: The only team(s) that won both matches in Stage-II is (are):
a. B
b. E & F
c. A, E & F
d. B, E & F
Sol: Option 'd' is correct.
Explanation: There are a total of 6C2
matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.
From the information given, we can conclude that the following matches were held in first stage:
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)
One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.
From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).Thus, the stage 1 matches are
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)
Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)
As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:
Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)
Hence, the teams that won both of their stage 2 matches are B, E and F.
Question 3: The teams that won exactly two matches in the event are:\
a. A, D & F
b. D & E
c. E & F
d. D & F
Sol: Option 'd' is correct.
Explanation: There are a total of 6C2 matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.
From the information given, we can conclude that the following matches were held in first stage:
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)
One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.
From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).
Thus, the stage 1 matches are
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)
Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:
Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)Hence, the wins by each team are A (3), B(4), C(0), D(2), E(4), F(2). Hence, D and F won exactly 2 matches.
Question 4: The team(s) with the most wins in the event is (are):
a. B & E
b. A & C
c. F
d. E
Sol: Option 'a' is correct.
Explanation: There are a total of 6C2 matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.
From the information given, we can conclude that the following matches were held in first stage:
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)
One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).
Thus, the stage 1 matches are
Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)
Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)
As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:
Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)
Hence, the wins by each team are A(3), B(4), C(0), D(2), E(4), F(2). Hence, most wins are by B and E.
Instructions: Answer the following questions based on the information given below
Example 2: The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goais scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Que 1: How many goals were scored in Match 7?
a. 3
b. 2
c. 1
d. 5
Sol: Option 'c' is correct.
Explanation: A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
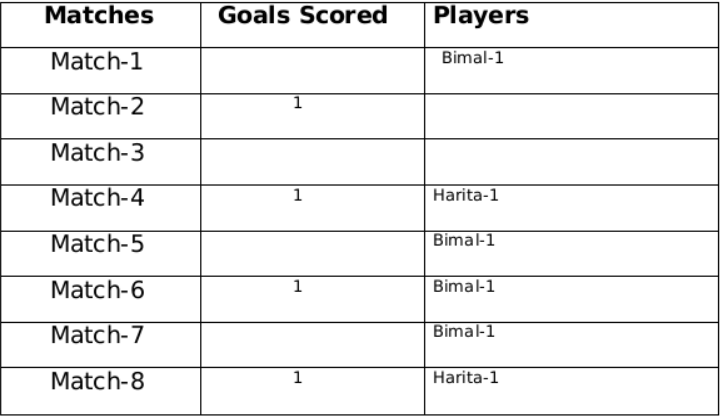
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following table:From statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1 then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2 then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches.
Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a = 1 b = 4 and c = 2
The remaining 3 goals were scored in the match 2, 3, 5 by Amla and Sarita in some order.
Que 2: Which of the following is the correct sequence of goals scored in the match 1,3,5 and 7?
a. 5, 1, 0, 1
b. 3, 1, 2, 1
c. 3, 2, 1, 2
d. 4, 1, 2, 1
Sol: Option 'd' is correct.
Explanation: A total of 12 goals were scored in 8 matches and each player scored atleast one goal and no of goals scored by each one of them is distinct so the possible number of goals scored by the players can be (1,2,3,6) or (1,2,4,5).
From statement 4 we know that Bimal scored 4 goals and since Harita scored more goals than Bimal so we can say that Harita scored 5 goals and the only case possible for total goals scored by each of the players is (1,2,4,5).
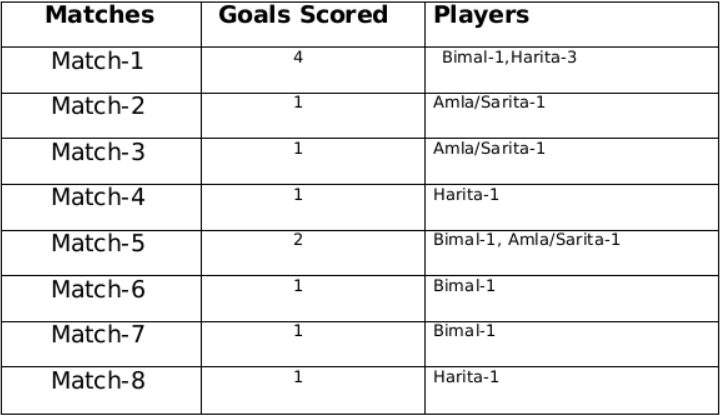
Now using statement 1, statement 3 and statement 4 we can say that the three consecutive matches in which Bimal scored will be 5th, 6th and 7th matches as Harita scored in 4th and 8th matches and we get the following tableFrom statement 5 and 6, we can conclude that the highest number of goals were scored in Match 1.
Let the no. of goals scored in 3rd and 7th match be a each and no. of goals scored in 1st and 5th match be b and c respectively.
Therefore, 2a + b + c = 8
If a = 1 then b + c = 6 therefore possible solutions for b and c will be 2 and 4 only
If a = 2 then b + c = 4 therefore possible solution for b and c will be 1 and 3 only but since highest goals scored is in Match 1 so then no. of goals scored in match 1 must be 3 and Harita must have scored 3 goals in match 1 as Harita scored 5 goals in exactly 3 matches. Therefore, we can see this is not possible because then the no. of goals scored in Match 1 becomes 4.
Therefore the only possible solution is a = 1 ,b = 4 and c = 2The remaining 3 goals were scored by Amla and Sarita in match 2, 3 and 5.
|
87 videos|180 docs|99 tests
|
FAQs on Types of Games and Tournaments - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| $1. What are the key analysis tools used for a tennis or badminton knockout tournament? |  |
| $2. How does a round robin tournament differ from a knockout tournament? |  |
| $3. What analysis tools are effective for a hockey or football round robin tournament? |  |
| $4. How can a cricket scorecard help in analyzing player performance? |  |
| $5. What is the advantage of using a round robin cum knockout tournament format? |  |