Introduction: Generic Puzzles | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Common Characteristics of Generic Puzzle Questions |

|
| Key Skills Required |

|
| How to Approach Generic Puzzles |

|
| Solved Examples |

|
Introduction
Generic puzzles refer to a broad category of logical reasoning problems that do not fall neatly into fixed types like seating arrangements or games & tournaments. They often involve:
- Scheduling: Assigning tasks, events, or people to specific time slots or roles based on constraints.
- Grouping & Selection: Forming teams or selecting individuals/items while adhering to rules (e.g., mutual exclusions or dependencies).
- Sequencing: Determining the correct order of events or items based on given conditions.
- Conditional Logic: Applying "if-then", "either-or", or "neither-nor" statements to deduce outcomes.
- Constraint-Based Problems: Solving scenarios where certain conditions must be satisfied (e.g., “A cannot be with B”, “C must be selected if D is selected”).

Common Characteristics of Generic Puzzle Questions
- Multiple Constraints: You're usually presented with 5–8 conditions that need to be applied simultaneously.
- No Fixed Template: Unlike seating arrangement or Venn diagram problems, there's no one-size-fits-all approach. Each puzzle demands fresh analysis.
- Option-Based Elimination: Most puzzles come with multiple-choice answers, allowing you to use elimination techniques effectively.
- Variable Complexity: Some puzzles are easy to crack with basic logic, while others require deep analysis and careful tracking of all possibilities.
Key Skills Required
To excel in generic puzzles, you need to develop the following abilities:
- Pattern Recognition: Identify recurring structures or rule-based logic within the problem.
- Logical Deduction: Apply deductive reasoning to narrow down valid combinations or sequences.
- Time Management: Learn to quickly assess whether a puzzle is worth investing time in or should be skipped.
- Visualisation: Use diagrams, tables, or grids to represent relationships and constraints clearly.
- Elimination Strategy: Rule out impossible options early to reduce complexity and speed up decision-making.
How to Approach Generic Puzzles
Step-by-Step Strategy
- Read the Entire Question Carefully: Understand all constraints before starting.
- List All Conditions: Write down each condition separately and note any dependencies.
- Start with the Most Restrictive Clue: Begin with clues that limit the number of possible arrangements.
- Build Scenarios: Create separate cases for different possibilities, especially when conditional statements are involved.
- Use Diagrams/Tables: Visualise the setup with placeholders or charts to track possibilities.
- Apply Elimination: As you go through answer choices, reject those that violate any rule.
- Re-evaluate After Each Step: Ensure every new piece of information aligns with previously established facts.
Solved Examples
The following illustrations provide step-by-step solutions to typical puzzle questions.
It is recommended to attempt solving the questions independently before consulting the detailed solutions provided.
Illustration 1
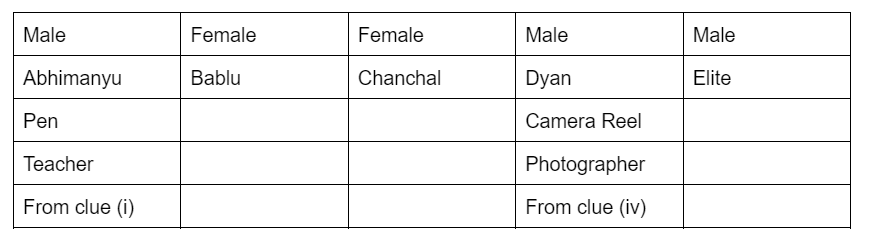
Direction: At a fancy dress party, Mr. Abhimanyu, Mrs. Bablu, Mrs. Chanchal, Mr. Dyan, and Mr. Elite attended. They dressed as specific objects representing their professions: a leaf, a pen, a fork, a camera reel, and a stethoscope. The corresponding professions were photographer, gardener, compounder, teacher, and cook.
Given clues:
(i) Mr. Abhimanyu is a teacher.
(ii) Neither Mrs. Bablu nor Mrs. Chanchal was dressed as a fork.
(iii) None of the men is a compounder.
(iv) Mr. Dyan is dressed as a camera reel.
(v) Mrs. Chanchal is a gardener.
(vi) Each person wore a costume relevant to his profession only. For example, the pen was worn by the teacher, the camera reel by the photographer, etc.
Que 1: Which person is dressed as a stethoscope?
(a) Mr. Abhimanyu
(b) Mrs. Bablu
(c) Mrs. Chanchal
(d) Mr. Dyan
Que 2: What is Mr. Elite's profession?
(a) Cook
(b) Gardener
(c) Compounder
(d) Teacher
Sol: Putting the direct clues (i) and (iv) in the table, we get:
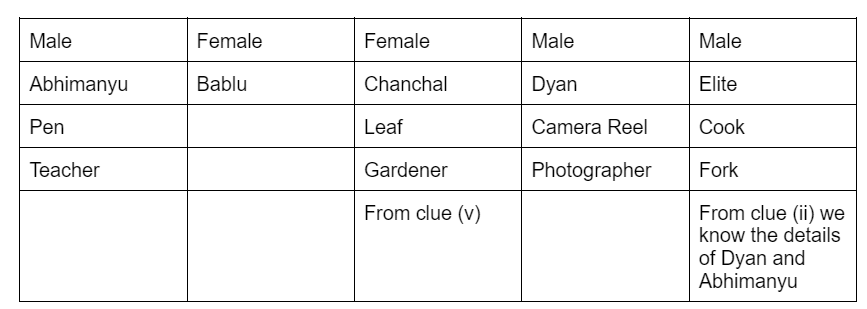
At this point, if we use clue (ii), it is evident that it must be Mr. Elite who is dressed as a fork. Also, using clue (v) Mrs. Chanchal is a gardener completes the solution.
Mrs. Bablu would be the compounder.
The solutions are:
Sol 1: Option (b) is correct.
Mrs. Bablu.
Sol 2: Option (a) is correct.
Elite is the cook.
Illustration 2
Direction: Read the information and answer the question.
Four engineers, designated as CE, SE, EE and AE, read a certain number of newspapers early in the morning.
One of them reads four newspapers, another reads three newspapers, the third reads two newspapers while the fourth one reads one newspaper. Below are some additional facts regarding the names of these officers:
(i) Naina is not the EE.
(ii) Hamleys is the AE.
(iii) Naina is not the CE and he reads more number of newspapers than Lalu.
(iv) The one who is the CE, reads more number of newspapers than Lalu .
(v) The person, who is the SE reads the maximum number of newspapers.
(vi) Bryan does not read two newspapers.
Que: Which of the following statements is necessarily true?
(a) Hamleys is the AE and reads two newspapers.
(b) Lalu is the EE and reads one newspaper.
(c) Bryan is the CE and reads three newspapers.
(d) Naina is the EE and reads four newspapers.
Sol: Hence, option (c) is the correct answer.
Explanation: From statement (ii), Hamleys is AE. From Statements (i) and (iii), Naina is not the CE or the EE.
Hence Naina is the SE and reads 4 newspapers as from Statement (v).
From statement (iv), Lalu is not the CE; this obviously means that Lalu is the EE and Bryan is the CE.
From statement (iv) and (vi),Bryan reads three newspapers.
As he reads more than at least one person, we cannot allocate one newspaper to him. Hence, Bryan must read three newspapers. Hence, the final distribution is as follows:
Engineer Name No. of Newspapers AE Hamleys 2/1 CE Bryan 3 SE Naina 4 EE Lalu 1/2
Solved Examples
Instructions for Questions 1-4
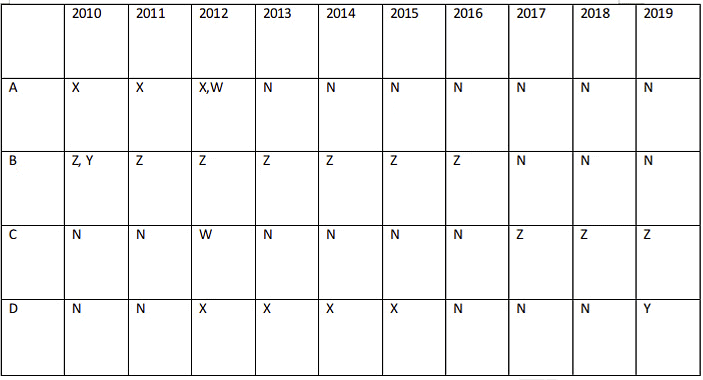
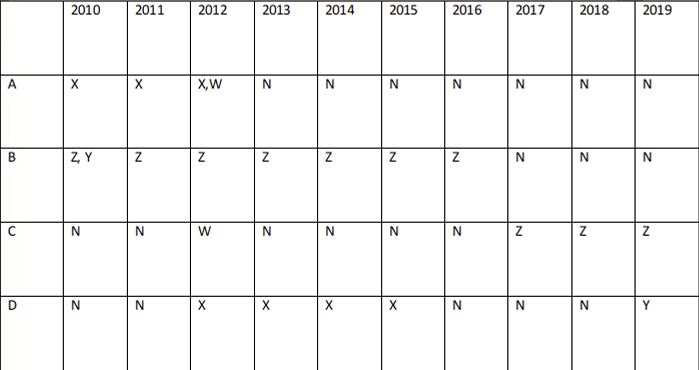
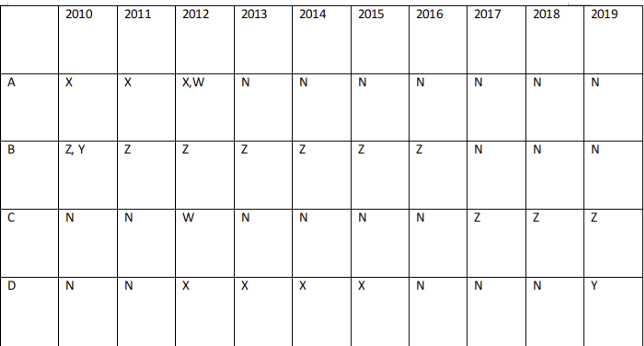
Four institutes, A, B, C, and D had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes. The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were ve contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Que 1: In which of the following years were there two or more contracts?
a. 2017
b. 2016
c. 2015
d. 2018
Sol: Option (c) is correct.
Explanation: From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From I, Z has at least one contract every year, the only possible combination is 7+3 or 7+4 year contract and that 7-year contract must be from B.
From III, Vendor W had contracts only in 2012 and from VII, Institutes B and D each had exactly one contract in 2012 => W has got contracts from A and C.
From II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that and from VI, VII: C and D didn't have any contract in 2011 and 2010 respectively => A should have X as a 3-year contract from 2010-2012. Now, for 2013-2015 X can't have B for the same. So, X must have got contracts from either C or D in that period.Case 1: X has C as a 3-year contract from 2013-2015 but in this case, D can't have any contract in 2012 so, this case is not valid.
Case 2: X has D for a 4-year contract from 2012-2015 and C must have Z for a three-year contract in the period 2017 2019 such that Z has at least one contract every year.
It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes => A hasn't got any contract from 2013-2019 as it has X, W in the period 2010-2012 and similarly, C shouldn't have any contracts in the years 2010, 2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in 2010 and 2019 and in 2010 D and C hasn't got any contract and A has already got 2 different contracts from two different vendors => Y has a contract from B in 2010 => B hasn't got any contracts in 2017, 2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.Now, the table looks like:
'N' represents no contract. Out of the given options, only 2015 has two contracts and rest have only one contract in that particular year
Que 2: Which institutes and vendors had more than one contracts in any year?
a. B, W, X, and Z
b. A, B, W, and X
c. A, D, W, and Z
d. B, D, W, and X
Sol: Option (b) is correct.
Explanation: From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.\
From I, Z has at least one contract every year, the only possible combination is 7+3 or 7+4 year contract and that 7-year contract must be from B.
From III, Vendor W had contracts only in 2012 and from VII, Institutes B and D each had exactly one contract in 2012 => W has got contracts from A and C.
From II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that and from VI, VII: C and D didn't have any contract in 2011 and 2010 respectively => A should have X as a 3-year contract from 2010-2012. Now, for 2013-2015 X can't have B for the same. So, X must have got contracts from either C or D in that period.Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can't have any contract in 2012 so, this case is not valid.Case 2:
X has D for a 4-year contract from 2012-2015 and C must have Z for a three-year contract in the period 2017 2019 such that Z has at least one contract every year.It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes => A hasn't got any contract from 2013-2019 as it has X, W in the period 2010-2012 and similarly, C shouldn't have any contracts in years 2010, 2013, 2014, 2015, 2016
From III, Vendor Y had contracts in 2010 and 2019 and in 2010 D and C hasn't got any contract and A has already got 2 different contracts from two different vendors => Y has a contract from B in 2010 => B hasn't got any contracts in 2017, 2018, 2019.
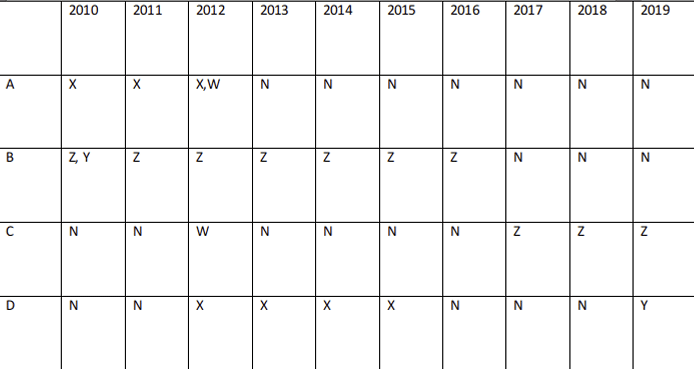
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018. Now, the table looks like:
'N' represents no contract. A, B, W, X had more than one contracts in a single year
Que 3: In how many years during this period was there only one contract?
a. 3
b. 2
c. 4
d. 5
Sol: Option (a) is correct.
Explanation: From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From I, Z has at least one contract every year, the only possible combination is 7+3 or 7+4 year contract and that 7-year contract must be from B.
From III, Vendor W had contracts only in 2012 and from VII, Institutes B and D each had exactly one contract in 2012 => W has got contracts from A and C.
From II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that and from VI, VII: C and D didn't have any contract in 2011 and 2010 respectively => A should have X as a 3-year contract from 2010-2012. Now, for 2013-2015 X can't have B for the same. So, X must have got contracts from either C or D in that period.Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can't have any contract in 2012 so, this case is not valid.Case 2:
X has D for a 4-year contract from 2012-2015 and C must have Z for a three-year contract in the period 2017 2019 such that Z has at least one contract every year.It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes => A hasn't got any contract from 2013-2019 as it has X, W in the period 2010-2012 and similarly, C shouldn't have any contracts in the years 2010, 2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in 2010 and 2019 and in 2010 D and C hasn't got any contract and A has already got 2 different contracts from two different vendors => Y has a contract from B in 2010 => B hasn't got any contracts in 2017, 2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:
'N' represents no contract. Only during 2016, 2017 and 2018, there was only one contract.
Que 4: Which of the following is true?
a. B had a contract with Z in 2017
b. B had a contract with Y in 2019
c. D had a contract with X in 2011
d. D had a contract with Y in 2019
Sol: Option (d) is correct.
Explanation: From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From I, Z has at least one contract every year, the only possible combination is 7+3 or 7+4 year contract and that 7-year contract must be from B.
From III, Vendor W had contracts only in 2012 and from VII, Institutes B and D each had exactly one contract in 2012 => W has got contracts from A and C.
From II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that and from VI, VII: C and D didn't have any contract in 2011 and 2010 respectively => A should have X as a 3-year contract from 2010-2012. Now, for 2013-2015 X can't have B for the same. So, X must have got contracts from either C or D in that period.Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can't have any contract in 2012 so, this case is not valid.Case 2:
X has D for a 4-year contract from 2012-2015 and C must have Z for a three-year contract in the period 2017 2019 such that Z has at least one contract every year.It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes => A hasn't got any contract from 2013-2019 as it has X, W in the period 2010-2012 and similarly, C shouldn't have any contracts in the years 2010, 2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in 2010 and 2019 and in 2010 D and C hasn't got any contract and A has already got 2 different contracts from two different vendors => Y has a contract from B in 2010 => B hasn't got any contracts in 2017, 2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.Now, the table looks like:
'N' represents no contract. Option D is true.
Instructions for Questions 5-8
Sixteen patients in a hospital must undergo a blood test for a disease. It is known that exactly one of them has the disease. The hospital has only eight testing kits and has decided to pool blood samples of patients into eight vials for the tests. The patients are numbered 1 through 16, and the vials are labelled A, B, C, D, E, F, G, and H. The following table shows the vials into which each patient’s blood sample is distributed.
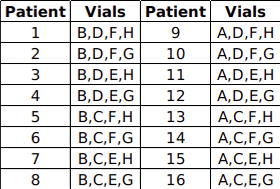
If a patient has the disease, then each vial containing his/her blood sample will test positive. If a vial tests positive, one of the patients whose blood samples were mixed in the vial has the disease. If a vial tests negative, then none of the patients whose blood samples were mixed in the vial has the disease.
Que 5: Suppose one of the lab assistants accidentally mixed two patients' blood samples before they were distributed to the vials. Which of the following correctly represents the set of all possible numbers of positive test results out of the eight vials?
a. {5,6,7,8}
b. {4,5,6,7}
c. {4,5,6,7,8}
d. {4,5}
Sol: Option (c) is correct.
Explanation: Let one of the patients, patient 1 or patient 16 has the disease and his blood is mixed with other them all 8 vials will tests positive.
⇒ 8 has to be one of the answers.
If patient 2 and patients 16’s blood is mixed of one of them has the disease then 7 of the 8 vials will test positive.
So 7 has to be there in the option.
If 1 has the disease and 1, 7 are mixed then 6 out the 8 vials tests positive.
If 1 has the disease and 1,9 are mixed then 5 of the 8 vials tests positive, Now, let us assume that patient 1 has the disease if his blood is not mixed, then 4 vials will definitely show positive. Hence, 3 is the correct answer.
Que 6: Which of the following combinations of test results is NOT possible?
a. Vials A and E positive, vials C and D negative
b. Vial B positive, vials C, F and H negative
c. Vials A and G positive, vials D and E negative
d. Vials B and D positive, vials F and H negative
Sol: Option (a) is correct.
Explanation: The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
If vials C and D negative, then no patient could test negative. Hence A is the correct answer.
Que 7: Suppose vial A tests positive and vials D and G test negative. Which of the following vials should we test next to identify the patient with the disease?
a. Vial B
b. Vial E
c. Vial C
d. Vial H
Sol: Option (b) is correct.
Explanation: The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
Suppose vial A tests positive and vials D and G test negative then the patient who tested positive must be one of patient 13 or 15.
Patient 13 or 15 are not present in vial B. So, A is not the answer.
Both patients present in vial C. Even if tested positive or negative we can't know who has got the disease. So, C is not the answer.
Both patients present in vial H. Even if tested positive or negative we can't know who has got the disease. So, H is not the answer.
Only patient 15 is present in vial E, if tested positive then patient 15 has the disease else patient 13 as disease.
Hence Option 2 is correct.
Que 8: Suppose vial C tests positive and vials A, E and H test negative. Which patient has the disease?
a. Patient 14
b. Patient 8
c. Patient 6
d. Patient 2
Sol: Option (c) is correct.
Explanation: The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
If vial C tests positive and vials A, E and H test negative then Patient 6 must have disease as all other patients in Vial C expect patient 6 are present in at least one of A, E, H. Therefore, option C is correct.
Instruction for Question 9-11:
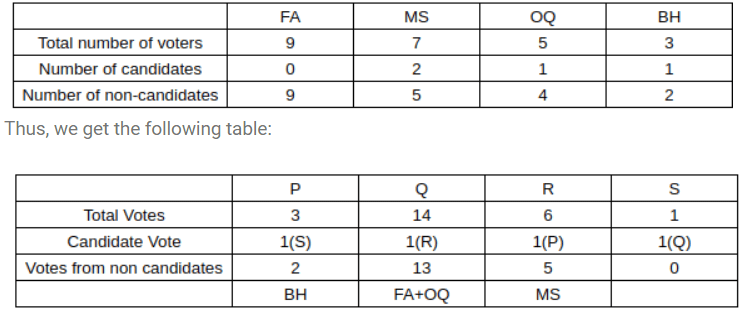
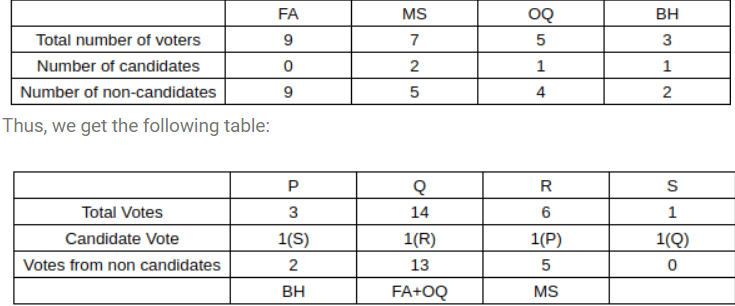
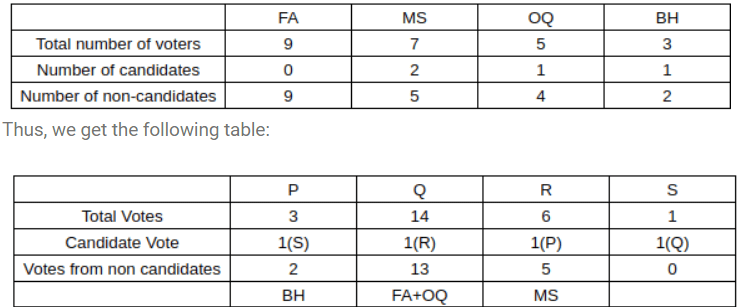
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O & Q
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi
Que 9: Which two candidates can belong to the same department?
a. Prof. Pakrasi & Prof. Qureshi
b. Prof. Pakrasi & Prof. Samuel
c. Prof. Qureshi & Prof. Ramaswamy
d. Prof. Ramaswamy & Prof. Samuel
Sol: Option 'a' is correct
Explanation: Now, we know there is only 1 candidate from 00, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
i. 105
ii. 4+1
iii.3+2
Considering case (1) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH.
This implies that the number of candidates in FA and MQ is 1, Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible
Since the maximum number of non-candidate voters a candidate can get is 13 (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (1), we know that 5+0 will happen only one when there are 5 non-candidates candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R.(1)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1
Now, if we consider Department MS, we know that there are 2 candidates from MS and R can't be one of them as the people in that department voted for him..... (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (P,S) and (Q,S) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.
Que 10: Which of the following can be the number of votes that Prof. Qureshi received from a single department?
a. 7
b. 6
c. 8
d. 9
Sol: Option 'd' is the correct answer.
Explanation: Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4.
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
1)5
ii)4+1
iii)3+2
Considering case (i) 4+1.
This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now, we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ.
Now, considering Case (i), we know that 5+0 will happen only once when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R(1)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1.Now, if we consider Department MS, we know that there are 2 candidates from MS and R can't be one of them as the people in that department voted for him.... (3 rd condition).So, the possible combinations of candidates in MS are (P,Q), (Q,S), (P,S)
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (PS) and (Q.S) as we know that S voted for P and Q voted for S).
So, we can infer that P and Q are from MSNow, we can see that the number of votes that Prof Qureshi received from a single department can be 9 or 5 (if R is from OQ) or 4 (if R is not from OQ).
So, among the options, only Option D can be true.
Que 11: If Prof. Samuel belongs to B&H, which of the following statements is/are true?
Statement A: Prof. Pakrasi belongs to M&S.
Statement B: Prof. Ramaswamy belongs to O&Q
a. Neither statement A nor statement B
b. Only statement B
c. Only statement A
d. Both statements A and B
Sol: Option 'd' is correct
Now, we know there is only 1 candidate from OQ, which means that the number of non-candidate voters in OQ will be 4,
We also know that the non-candidates in a particular department voted as a block, and we also know that the least number of non-candidate voters in a particular department can be 1 (BH, 3-2 faculty).
Now, we also know that R got 5 votes from non-candidates.
Now we can write 5 as
1)5
ii)4+1
iii)3+2
Considering case (i) 4+1. This is only possible when there is 1 candidate from OQ, and there are 2 candidates from BH. This implies that the number of candidates in FA and MQ is 1. Now, if we consider FA and MQ and put only 1 candidate there, it implies that there are 15 non-candidate voters between them. Now we know this is not possible since the maximum number of non-candidate voters a candidate can get is 13. (Please note that non-candidates of a particular department vote as a block).
On similar grounds, we can eliminate Case (iii) as it also implies there is only 1 candidate in FA and MQ
Now, considering Case (1), we know that 5+0 will happen only one when there are 5 non-candidates in a single department. This is only possible in MS (Out of 7, there will be 2 candidates and 5 non-candidates).
So we can conclude that MS has 2 candidates and that they voted Prof. R(0)
We also know that Prof P got 2 votes from Non-candidates. This is only possible when BH has 1 candidate.
So, we can conclude that the number of professors in FA, MS, OQ, BH is 0,2,1,1Now, if we consider Department MS, we know that there are 2 candidates from MS and R can't be one of them as the people in that department voted for him..... (3 rd condition).
So the possible combinations of candidates in MS are (P,Q), (Q,S), (PS).
Now we also know that no one can vote for a candidate in their own department, so we can eliminate (PS) and (QS) as we know that S voted for P and Q voted for S).
So we can infer that P and Q are from MS.We have been told Prof Samuel belongs to B&H. So we have to consider only Case 1. In Case 1 we can see that Prof Prakash belongs to MS and Prof Ramaswamy belongs to OQ.
Therefore, both the statements are true.
|
98 videos|160 docs|99 tests
|
FAQs on Introduction: Generic Puzzles - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are generic puzzles in the context of CAT preparation? |  |
| 2. How can I improve my skills in solving generic puzzles for the CAT? |  |
| 3. Are there specific types of generic puzzles that frequently appear in the CAT exam? |  |
| 4. How should I approach a generic puzzle during the CAT exam? |  |
| 5. Can practicing generic puzzles help in other sections of the CAT exam? |  |