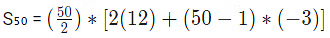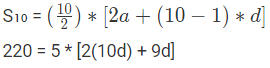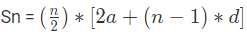Important Formulas: Arithmetic Progressions | Quantitative Aptitude for SSC CGL PDF Download
Arithmetic Progression (AP)
An arithmetic progression, also known as an arithmetic sequence, is a sequence of numbers in which the difference between two consecutive members remains constant.

Basic Concept on Arithmetic Progression
First term is denoted by a Common difference is denoted by d nth term is denoted by
an or tn
Sum of the First n terms is denoted by Sn
Example : 4,8,12,16……
Formula of Arithmetic Progression
1. nth term of an AP
Formula to find the nth term of an AP is
Tn = a + (n – 1) d
where tn = nth term,
a = first term ,
d = common difference,
n = number of terms in the sequence.
2. Number of terms in an AP
Formula to find the numbers of term of an AP is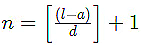 where n = number of terms,
where n = number of terms,
a = first term,
l = last term,
d= common difference.
3. Sum of the First n terms in an AP
Formula to find the sum of first n terms of an AP is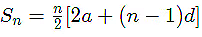 or
or where,a = first term,
where,a = first term,
d = common difference,
tn = nth term = a + (n-1)d
4. Arithmetic Mean
If a, b, c are in AP, then the Arithmetic mean of a and c is b i.e.
Some other Important Formulas of Arithmetic Progression
1. Sum of first n natural numbers
We derive the formula to find the sum of first n natural numbers whereS = Sum of first n natural numbers
whereS = Sum of first n natural numbers
n = number of First n natural numbers
2. Sum of Squares of first n natural numbers
Formula to find the sum of squares of the first n natural numbers is ,whereS = Sum of Squares of first n natural numbers
,whereS = Sum of Squares of first n natural numbers
n = number of First n natural numbers.
3. Sum of first n odd numbers
S = n2
where
S = Sum of first n odd numbers
n = number of First n odd numbers.
4. Sum of first n even numbers
S = n(n+1)
where
S = Sum of first n Even numbers
n = number of First n Even numbers.
Using Formulas of Arithmetic Progression in Questions
Q1: The sum of the first 20 terms of an arithmetic progression is 610, and the sum of the next 30 terms is 2130. What is the common difference of this arithmetic progression?
(a) 8
(b) 10
(c) 12
(d) 15
Ans: (b)
Let the first term of the arithmetic progression be ‘a’ and the common difference be ‘d’. The sum of the first 20 terms is given by:
The sum of the next 30 terms is:
Given S1 = 610 and S₂ = 2130, we can write two equations:
20a + 190d = 610
30a + 590d = 2130
Solving these equations, we get d = 10. Therefore, the correct answer is (b) 10.
Q2: The sum of the first 50 terms of an arithmetic progression is 4800. If the first term is 12 and the common difference is -3, find the 30th term.
(a) -14
(b) -17
(c) -20
(d) -75
Ans: (d)
The sum of the first 50 terms of the arithmetic progression is given by:
Solving, we get S50 = 4800.
Now, to find the 30th term, we can use the formula for the nth term of an AP:
a30 = a + (n-1) * d
a30 = 12 + (30-1) * (-3)
a30 = 12 – 87
a30 = -75.
The correct answer is -75.
Q3: The 10th term of an arithmetic progression is equal to three times the 6th term. If the sum of the first 10 terms is 220, what is the common difference of the progression?
(a) 6
(b) 8
(c) 10
(d) 12
Ans: (b)
Let the first term of the arithmetic progression be ‘a’, and the common difference be ‘d’.
According to the problem, a + 9d = 3(a + 5d)
Solving this equation, we get a = 10d.
Now, the sum of the first 10 terms of the arithmetic progression is given by:
Solving this equation, we get d = 8.
Therefore, the correct answer is (B) 8.
Q4: In an arithmetic progression, the 15th term is 8 more than the 8th term. If the common difference is 3, what is the 10th term of the progression?
(a) 21
(b) 23
(c) 25
(d) 40
Ans: (d)
Let the first term of the arithmetic progression be ‘a’. Then, the 8th term is given by a + 7 * 3 = a + 21, and the 15th term is a + 14 * 3 = a + 42.
According to the problem, a + 42 = (a + 21) + 8
Solving this equation, we get a = 13.
Now, the 10th term is a + 9 * 3 = 13 + 27 = 40.
The correct answer is 40.
Q5: If the sum of the first ‘n’ terms of an arithmetic progression is given by Sn = 5n2 + 3n, what is the first term of the progression?
(a) 2
(b) 5
(c) 7
(d) 4
Ans: (d)
The sum of the first ‘n’ terms of an arithmetic progression is given by:
Comparing it with Sn = 5n2 + 3n, we get 2a + (n-1) * d = 5n + 3
Since we are looking for the first term ‘a’, we can consider ‘n’ as 1:
2a + (1-1) * d = 5 + 3
2a = 8
a = 4.
The correct answer is 4.
|
342 videos|298 docs|185 tests
|
FAQs on Important Formulas: Arithmetic Progressions - Quantitative Aptitude for SSC CGL
| 1. What is an arithmetic progression? |  |
| 2. How can I find the nth term of an arithmetic progression? |  |
| 3. Can an arithmetic progression have a negative common difference? |  |
| 4. What is the formula for finding the sum of an arithmetic progression? |  |
| 5. How can I determine if a given sequence is an arithmetic progression? |  |