Important Concepts: Team Formations | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Key Concepts |

|
| Tips and Tricks for Solving Team Formation Questions |

|
| Solved Examples |

|
Introduction
Team Formation is a vital topic in the Logical Reasoning (LR) section of the Common Admission Test (CAT) Exam, which is a key entrance exam for MBA programs in India, particularly for admission to the Indian Institutes of Management (IIMs).
These questions require you to form teams or groups from a set of individuals or objects while adhering to specific conditions. They test your ability to interpret complex constraints, organize information logically, and derive valid team compositions. This guide explains Team Formation in a simple, student-friendly manner with examples and strategies to help you excel in the CAT Exam.
- Visualising the Team Layout
Quickly sketch or imagine the overall team structure: how many groups there are, the size of each, and which slots are open. A clear mental picture (or diagram) of “empty chairs” lets you place individuals or objects more effectively. - Sequencing Clues Systematically
Not all hints arrive in the order you’ll use them. Learn to reorder statements by priority—e.g., group-size constraints first, mutual-inclusion/exclusion next, then individual conditional rules. - Spotting and Timing Indirect Clues
Some clues only become relevant after other placements are made. Train yourself to recognise when a seemingly “extra” hint should be applied, resisting the urge to force every clue into play immediately. - Applying Logical-Reasoning Principles
Ground your work in formal reasoning rules:
1. Implication (if-then)
2. Bi-conditional (if and only if)
3. Mutual exclusion (cannot coexist)
Systematic use of these principles ensures you neither miss nor misapply any constraint.

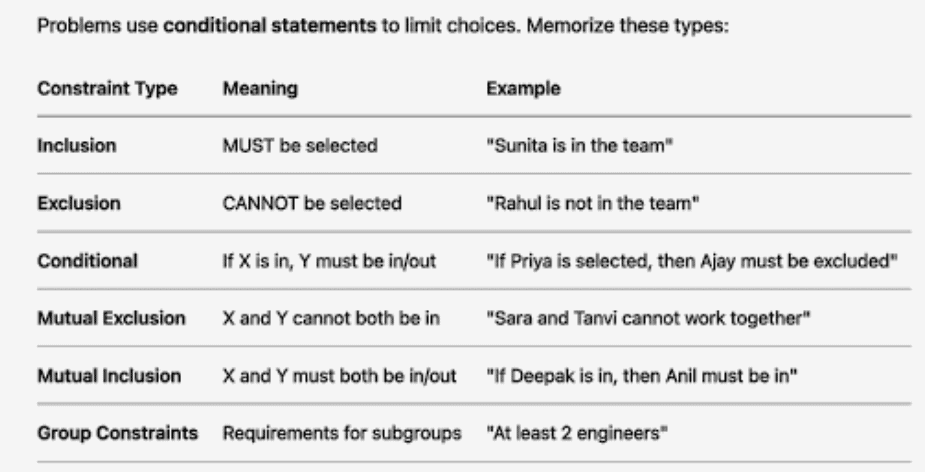
Key Concepts
Understanding the following concepts is critical for solving Team Formation questions effectively:
1. Conditions for Selection
These define how many members can or must be selected from a group. Common phrases include:
- At least one: One or more members must be selected (1+).
- At most one: Zero or one member can be selected (0 or 1).
- Exactly one: Precisely one member must be selected.
- At most two: Zero, one, or two members can be selected (0, 1, or 2).

2. Logical Implications
These conditions establish relationships between selections, often using logical connectors. Key examples include:
- A selected implies B selected.
- A cannot be selected without B.
- B can be selected without A.
- If B is not selected, A cannot be selected.
- B selected implies A selected.
- If A is not selected, B cannot be selected.
- If A is selected, B cannot be selected.
- If B is selected, A cannot be selected.
3. Constraints
These include specific rules, such as:
- Pairings: Certain members must be in the same group (e.g., A and B must be together).
- Exclusions: Certain members cannot be in the same group (e.g., A and C cannot be together).
- Gender or Category Separation: For example, "no adults of the same gender can be together" requires strict separation by gender.
4. Group Size and Composition
The number of members in each group may be fixed (e.g., exactly three per group) or variable, depending on the question. Some questions may also specify the total number of groups or members available.
5. Contextual Scenarios
Questions may involve real-world scenarios, such as:
- Assigning portfolios in a government.
- Forming sports teams with match schedules.
- Grouping employees for a project with role constraints.
The following table summarizes common condition types and their implications:
Tips and Tricks for Solving Team Formation Questions
Team Formation questions can be complex due to multiple conditions, but the following strategies can help you solve them efficiently:
1. Start with Group Size Constraints First
Always begin by fixing the number and size of each team based on given data. This narrows down possibilities and prevents contradiction later.
2. Use Tables or Grid Diagrams
For multi-group problems, create a simple table or matrix. This visual aid helps track who is placed, who is excluded, and highlights available spots quickly.
3. Prioritise Definite Clues Over Conditional Ones
Use clues with certainty (e.g., “A is in Team 1”) before those with conditions (“B is with C only if D is in Team 2”). This builds a solid base before handling dependencies.
4. Exploit Mutually Exclusive Pairs
Clues like “A and B cannot be in the same team” are powerful. Use them to eliminate options early and reduce complexity.
5. Plug and Eliminate Using Options (if available)
In MCQs, test each option quickly against key clues. Even in TITA questions, consider possible team configurations and eliminate invalid ones by applying constraints.
The following table provides a quick reference for applying these tips:

Solved Examples
Que 1:Directions for Questions 1 to 3:
Three adult women (R, S, and T), two adult men (U and V), and four children (W, X, Y, and Z) are going to watch a movie. Though, during the online booking of the tickets, they realized that the nine seats available for the show are in three different classes —Silver Class, Gold Class and Lounge. The layout also showed that in each class, three adjacent seats are available.
To watch the movie, they decide to have the three groups of three members each as per the following conditions:
No adults of the same gender can be together in One group.
W cannot be in R’s group.
X must be in a group with S or U, or both.
1. If R is the only adult in one group, the other members of her group must be
(a) W and Y
(b) X and Y
(c) X and Z
(d) Y and Z
2. Which of the following pairs of people can be in the same group as W?
(a) R and Y
(b) S and U
(c) S and V
(d) U and V
3. Any of the following pairs of people could be in a group with X, except:
(a) R and U
(b) S and T
(c) S and U
(d) S and W
Sol:
Let us understand the constraints.Persons
Total Persons: 9
- Women: R, S, T
- Men: U, V
- Children: W, X, Y, Z
Problem Context
The nine individuals are booking movie tickets for a show with nine seats in three classes (Silver, Gold, Lounge), each with three adjacent seats. They must form three groups of three members each, corresponding to the seating classes, while adhering to the following constraints:
Constraints
- No adults of the same gender can be in the same group.
- W cannot be in R’s group.
- X must be in a group with S or U or both.
The following table summarises the constraints:
Group Distribution
With 5 adults (3 women, 2 men) and 4 children, the groups must be distributed as follows:
- Group 1 (G1): 2 adults (1 man, 1 woman) + 1 child
- Group 2 (G2): 2 adults (1 man, 1 woman) + 1 child
- Group 3 (G3): 1 adult (a woman) + 2 children
This distribution is necessary because:
- Total adults: 5 (2 men, 3 women).
- Total children: 4.
- Only 2 men (U, V) are available, so only 2 groups can have a man, each paired with a woman.
- The third group must have the remaining woman and 2 children.
Ans 1:
Scenario: R is the only adult in a group, so R is in G3 (1 adult + 2 children).Constraints Analysis:
- W cannot be in R’s group, so W cannot be in G3.
- X must be in a group with S or U or both. Since G3 has only R, X cannot be in G3 (no S or U).
- Available children for G3: Y, Z (since W and X are excluded).
Group Setup:
- G3: R, Y, Z
- G1 and G2: Must include U, V, S, T, and the remaining children (W, X).
Option Analysis:
- (a) W and Y: W cannot be with R, so invalid.
- (b) X and Y: X cannot be in G3 (X must be with S or U), so invalid.
- (c) X and Z: X cannot be in G3, so invalid.
- (d) Y and Z: Valid, as Y and Z are the only children who can be with R.
Example Configuration:
- G1: U, S, X (X with S and U)
- G2: V, T, W
- G3: R, Y, Z
Verification:
- No same-gender adults: G1 (U, S), G2 (V, T), G3 (R only).
- W not with R: W in G2, R in G3.
- X with S or U: X in G1 with S and U.
Answer: (d) Y and Z
Ans 2:
Scenario: Identify which pair can be in the same group as W.Constraints Analysis:
- W cannot be with R, so W must be in G1 or G2 (if R is in G3) or in G3 (if R is in G1 or G2).
- The pair must be valid within a group of three, respecting all constraints.
Option Analysis:
- (a) R and Y: W cannot be with R, so R cannot be in W’s group. Invalid.
- (b) S and U: S (woman) and U (man) can be together in G1 or G2. However, if S and U are in a group (e.g., G1: U, S, ?), X must be in that group (X must be with S or U). Thus, the group is U, S, X, leaving no room for W. Invalid.
- (c) S and V:S (woman) and V (man) can be together. Example configuration:
Valid.
- G1: U, T, X (X with U)
- G2: V, S, W (W with S and V)
- G3: R, Y, Z
- Verification:
- No same-gender adults: G1 (U, T), G2 (V, S), G3 (R).
- W not with R: W in G2, R in G3.
- X with S or U: X in G1 with U.
- (d) U and V: U and V are both men, so they cannot be in the same group (no same-gender adults). Invalid.
Answer: (c) S and V
Ans 3:
Scenario: Identify which pair cannot be in a group with X.Constraints Analysis:
- X must be in a group with S or U or both, so X can only be in G1 or G2 (where S or U are present).
- The pair must be valid within a group of three, respecting all constraints.
Option Analysis:
- (a) R and U:R (woman) and U (man) can be together. Example:
Valid.
- G1: U, R, X (X with U)
- G2: V, S, W
- G3: T, Y, Z
- Verification:
- No same-gender adults: G1 (U, R), G2 (V, S), G3 (T).
- W not with R: W in G2, R in G1.
- X with S or U: X in G1 with U.
- (b) S and T: S and T are both women, so they cannot be in the same group (no same-gender adults). Thus, they cannot be in a group with X. Invalid.
- (c) S and U:S (woman) and U (man) can be together. Example:
Valid.
- G1: U, S, X (X with S and U)
- G2: V, T, W
- G3: R, Y, Z
- Verification:
- No same-gender adults: G1 (U, S), G2 (V, T), G3 (R).
- W not with R: W in G2, R in G3.
- X with S or U: X in G1 with S and U.
- (d) S and W:S (woman) and W (child) can be together. Example:
Valid.
- G1: U, R, Y
- G2: V, T, Z
- G3: S, X, W (X with S)
- Verification:
- No same-gender adults: G1 (U, R), G2 (V, T), G3 (S only).
- W not with R: W in G3, R in G1.
- X with S or U: X in G3 with S.
Answer: (b) S and T
Que 2: Directions for Questions 1 to 3:
(i) A home stay has 6 rooms A, B, C, D, E and F. Among these, A and C can accommodate two persons each; the rest can accommodate only one each.
(ii) Eight guests P, Q, R, S, T, U, W and X are to be kept in these rooms. Q, T and X are females while the rest are males. The two sexes can't be put together in the same room. No man is willing to stay in room C or F.
(iii) P wants to be alone but does not want to stay in rooms B or D. S needs a partner but is not ready to stay with U or W. X does not want to share her room.
Q1: Who among the following will stay in room E?
(a) U
(b) W
(c) P
(d) Data inadequate
Ans: (c)
Q2: In which of the following rooms will U stay?
(a) B
(b) D
(c) А
(d) B or D
Ans: (d)
Q3: X will stay in which of the following rooms?
(a) C
(b) F
(c) B
(d) Data inadequate
Ans: (b)
Solutions:
Initial information:
A (2)
B (1)
C (2)
D (1)
E (1)
F (1)
Also, P+, Q, R*, S*, T, U*, W, X. From clue (ii), Room C (2 people) and Room F (1 person) should be women's rooms as men cannot be placed there. From clue (iii P must be in E, S must be in A (where U and W cannot be).
Thus, S must be sharing his room with R. Also, U and W must be in some random order in Rooms B or D. Also, X must be in Room F as she is a female and wants a single room.
Collating all this, we get:
A (2) S, R
B (1)
C (2) Q, T
D (1)
E (1) Р
F (1) X
Hence, the answers are:
1. P (c)
2. B or D (d)
3. F (b)
Que 3: Directions for Questions 1 to 3:
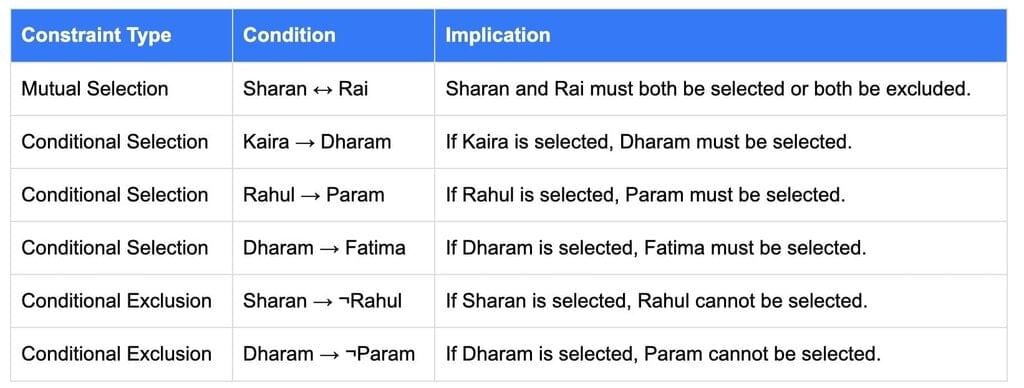
A group of three or four has to be selected from seven persons. Among the seven, there are two women, Fatima and Kaira, and five men - Rahul, Sharan, Dharam, Param and Rai. Rahul would not like to be in the group if Sharan is also selected. Sharan and Rai want to be selected together in the group. Kaira would like to be in the group only if Dharam is also there. Dharam, if selected, would not like Param in the group. Rahul would like to be in the group only if Param is also there. Dharam insists that Fatima must be selected in case he is there in the group.
Q1: Which of the following is a feasible group of three?
(a) Dharam, Rahul, Rai
(b) Param, Sharan, Rai
(c) Kaira, Dharam, Sharan
(d) Fatima, Dharam, Rahul
Ans: (b)
Q2: Which of the following is a feasible group of four?
(a) Rahul, Param, Fatima, Rai
(b) Sharan, Rai, Kaira, Dharam
(c) Sharan, Rai, Fatima, Dharam
(d) Fatima, Dharam, Rahul, Param
Ans: (c)
Q3: Which of the following statements is true?
(a) Kaira and Rahul can be part of a group of four.
(b) A group of four can have two women.
(c) A group of four can have all four men.
(d) None of the above.
Ans: (d)
Solutions:
Total Persons: 7
- Women: Fatima, Kaira
- Men: Rahul, Sharan, Dharam, Param, Rai
Constraints
The selection of the group must satisfy the following constraints:
1. Mutual Selection
- Sharan and Rai must be selected together (i.e., both must be included or both must be excluded).
2. Conditional Selections
- If Kaira is selected, then Dharam must also be selected.
- If Rahul is selected, then Param must also be selected.
- If Dharam is selected, then Fatima must also be selected.
3. Conditional Exclusions
- If Sharan is selected, then Rahul cannot be selected.
- If Dharam is selected, then Param cannot be selected.
The following table summarises the constraints for quick reference:
Ans 1:
We need a group of three that satisfies all constraints.
- Option (a): Dharam, Rahul, Rai
- Rai is selected, but Sharan is not, violating Constraint 1 (Sharan ↔ Rai).
- Invalid.
- Option (b): Param, Sharan, Rai
- Sharan and Rai are both selected, satisfying Constraint 1.
- Kaira is not selected, so Constraint 2a is not applicable.
- Rahul is not selected, so Constraint 2b is not applicable.
- Dharam is not selected, so Constraints 2c and 3b are not applicable.
- Sharan is selected, so Rahul cannot be selected (Constraint 3a), and Rahul is not selected, satisfying this.
- All constraints are satisfied. Valid.
- Option (c): Kaira, Dharam, Sharan
- Kaira is selected, so Dharam must be selected (Constraint 2a), and he is, satisfying this.
- Dharam is selected, so Fatima must be selected (Constraint 2c), but Fatima is not in the group, violating this.
- Invalid.
- Option (d): Fatima, Dharam, Rahul
- Dharam is selected, so Fatima must be selected (Constraint 2c), and she is, satisfying this.
- Dharam is selected, so Param cannot be selected (Constraint 3b), and Param is not selected, satisfying this.
- Rahul is selected, so Param must be selected (Constraint 2b), but Param is not selected, violating this.
- Invalid.
Answer: (b) Param, Sharan, Rai is the feasible group of three.
Ans 2:
We need a group of four that satisfies all constraints.
- Option (a): Rahul, Param, Fatima, Rai
- Rai is selected, but Sharan is not, violating Constraint 1 (Sharan ↔ Rai).
- Invalid.
- Option (b): Sharan, Rai, Kaira, Dharam
- Sharan and Rai are both selected, satisfying Constraint 1.
- Kaira is selected, so Dharam must be selected (Constraint 2a), and he is, satisfying this.
- Dharam is selected, so Fatima must be selected (Constraint 2c), but Fatima is not in the group, violating this.
- Invalid.
- Option (c): Sharan, Rai, Fatima, Dharam
- Sharan and Rai are both selected, satisfying Constraint 1.
- Kaira is not selected, so Constraint 2a is not applicable.
- Rahul is not selected, so Constraint 2b is not applicable.
- Dharam is selected, so Fatima must be selected (Constraint 2c), and she is, satisfying this.
- Sharan is selected, so Rahul cannot be selected (Constraint 3a), and Rahul is not selected, satisfying this.
- Dharam is selected, so Param cannot be selected (Constraint 3b), and Param is not selected, satisfying this.
- All constraints are satisfied. Valid.
- Option (d): Fatima, Dharam, Rahul, Param
- Dharam is selected, so Param cannot be selected (Constraint 3b), but Param is selected, violating this.
- Invalid.
Answer: (c) Sharan, Rai, Fatima, Dharam is the feasible group of four.
Ans 3:
We need to determine which statement is true.
- Option (a): Kaira and Rahul can be part of a group of four.
- If Kaira is selected, then Dharam must be selected (Constraint 2a).
- If Rahul is selected, then Param must be selected (Constraint 2b).
- If Dharam is selected, then Param cannot be selected (Constraint 3b).
- This creates a contradiction: selecting both Kaira and Rahul requires both Dharam and Param, but Dharam and Param cannot be selected together.
- Therefore, Kaira and Rahul cannot be part of a group of four. False.
- Option (b): A group of four can have two women.
- The two women are Fatima and Kaira.
- If Kaira is selected, then Dharam must be selected (Constraint 2a).
- If Dharam is selected, then Fatima must be selected (Constraint 2c), which is satisfied since Fatima is one of the two women.
- So, we have Fatima, Kaira, Dharam, and need one more person from Rahul, Sharan, Rai, or Param.
- However, Dharam is selected, so Param cannot be selected (Constraint 3b), leaving Rahul, Sharan, or Rai.
- If Rahul is selected, then Param must be selected (Constraint 2b), but Param cannot be selected, so Rahul cannot be selected.
- If Sharan is selected, then Rai must be selected (Constraint 1), but that would make five people (Fatima, Kaira, Dharam, Sharan, Rai), which exceeds four.
- If Rai is selected, then Sharan must be selected (Constraint 1), again leading to five people.
- Thus, no fourth person can be selected without violating constraints or exceeding four members.
- Therefore, a group of four cannot have both women. False.
- Option (c): A group of four can have all four men.
- The problem states there are five men (Rahul, Sharan, Dharam, Param, Rai), but the option likely refers to selecting four men, as "all four men" suggests a group of four.
- Suppose we select four men, e.g., Rahul, Sharan, Param, Rai.
- Sharan is selected, so Rahul cannot be selected (Constraint 3a), but Rahul is selected, violating this.
- Try another combination, e.g., Rahul, Param, Rai, Dharam.
- Rahul is selected, so Param must be selected (Constraint 2b), which is satisfied.
- Dharam is selected, so Param cannot be selected (Constraint 3b), but Param is selected, violating this.
- Try Sharan, Rai, Param, Rahul.
- Sharan and Rai are selected, satisfying Constraint 1.
- Sharan is selected, so Rahul cannot be selected (Constraint 3a), but Rahul is selected, violating this.
- Any combination including Dharam requires Fatima (Constraint 2c), introducing a woman, so we cannot have only men.
- Thus, a group of four cannot consist of four men. False.
- Option (d): None of the above.
- Since options (a), (b), and (c) are all false, option (d) is true.
Answer: (d) None of the above.
|
77 videos|180 docs|96 tests
|
FAQs on Important Concepts: Team Formations - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are keywords and why are they important in the context of search engine optimization? |  |
| 2. How can I determine the right keywords to use for my website? |  |
| 3. What is the role of long-tail keywords in SEO? |  |
| 4. How should I use keywords on my website without over-optimizing? |  |
| 5. How frequently should I update my keywords for SEO purposes? |  |