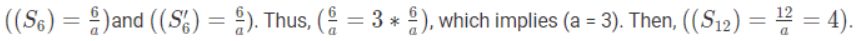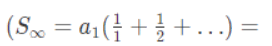Important Formulas: Harmonic Progressions | Quantitative Aptitude for SSC CGL PDF Download
Definition of Harmonic Progression(HP)
- A sequence of numbers is said to be a harmonic progression if the reciprocal of the terms are in arithmetic progression.
- If a, b, c, d, e, f is in arithmetic progression, then the harmonic progression can be written as 1/a, 1/b, 1/c, 1/d, 1/e, 1/f.

Formulas of Harmonic Progression (HP)
- If the arithmetic progression is written in the form:
a, a + d, a + 2d, a + 3d, …, a + (n – 1)d
Then the harmonic progression formula is as follows:
1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), …
where,
First term = a
Common difference = d - To determine the harmonic progression problems, the first thing we need to do is to obtain the corresponding arithmetic progression sum.
It means that the nth term of the harmonic progression is equivalent to the reciprocal of the nth term of the analogous A.P. - Formula for nth term of the harmonic progression series is: nth term/General Term
(aₙ) = 1 / [a + (n – 1)d]
where:
“a” is the first term of A.P
“d” is the common difference
“n” is the number of terms in A.P Harmonic Mean (HM)
Harmonic Mean is type of numerical average, which is calculated by dividing the number of observation by the reciprocal of each number in series.
If a, b are in HP, then there HM is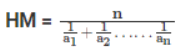
Where, n = Total number of numbers or terms, a1, a2,…..an = Individual terms or individual values.
Harmonic Mean of two numbers a and b is
Harmonic Mean of three numbers a, b and c is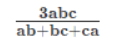
- Sum of n terms in Harmonic Progression is
For: 1/a, 1/(a + d), 1/(a + 2d), …, 1/[a + (n – 1)d
Sₙ = (1/d) x ln [(2a + (2n – 1)d) / (2a – d)] Relation Between Arithmetic Mean, Geometric Mean, and Harmonic Mean
To understand the relation between arithmetic mean, geometric mean, and harmonic mean, we must know the formulas of all these three types of means.
Consider that p and q are the two numbers and the number of values = 2, thenArithmetic Mean Formula = (p + q) / 2
⇒ 1/AM = 2 / (p + q) ---- (equation 1)
Geometric Mean Formula = √(p × q)
⇒ GM² = p × q ---- (equation 2)
Harmonic Mean Formula = 2 / (1/p + 1/q)
⇒ HM = 2 / [(p + q) / (p × q)]
⇒ HM = (2 × p × q) / (p + q) ---- (equation 3)
Now, substitute equations 1 and 2 in equation 3
HM = (GM² / AM)
or ⇒ GM² = AM × HM
or ⇒ GM = √(AM × HM) MCQ: Harmonic Progressions
MCQ: Harmonic ProgressionsStart Test Start TestHarmonic Sequence
A sequence of numbers is said to be in a harmonic sequence if the reciprocals of all the elements/numbers/data of the sequence form an arithmetic sequence.
Harmonic sequence:
1/a₁, 1/a₂, 1/a₃, … , 1/aₖ
Example of Harmonic Sequence
1/3, 1/6, 1/9, 1/12, 1/15
Here, the reciprocals of all the terms are in the arithmetic sequence
3, 6, 9, 12, 15
Also, if the sequence a, b, c, d, … is assumed to be an arithmetic sequence, then the harmonic sequence can be written as:
1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), …
Examples
Example 1: In a harmonic progression, the sum of the first 5 terms is 6, and the sum of their cubes is 405. What is the first term of this progression?
(a) (1/3)
(b) (1/4)
(c) (1/5)
(d) (1/6)
Ans: (a)
Let a be the first term and d be the common difference of the harmonic progression.
The sum of the first 5 terms is given by ((S5) = 5a + 10d = 6). The sum of their cubes is given by (Scubes) = a3 + (a + d) 3 + (a + 2d)3 + (a + 3d)3 + (a + 4d)3 = 405).
Using the value of ((S5)), we can solve for d, and then using ((Scubes )),
we can solve for a, which turns out to be (1/3).
Example 2: In a harmonic progression, the sum of the first 6 terms is 3 times the sum of their reciprocals. What is the sum of the first 12 terms of this progression?
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (c)
Let (Sn) be the sum of the first n terms and (Sn′) be the sum of the reciprocals of the first n terms. The given condition can be written as ((S6) = (3S6′)). Using the formula for the sum of the first n terms of a harmonic progression, we have
Example 3: The sum of an infinite harmonic progression is (5/3). What is the sum of the squares of the terms in this progression?
(a) (10/3)
(b) (25/9)
(c) (15/4)
(d) (9/5)
Ans: (a)
The sum of the squares of the terms in a harmonic progression is given bywhere a1 is the first term. Given the sum of the infinite harmonic progression as (5/3), we can use the result
Example 4: In a harmonic progression,  . What is the sum of the first 10 terms of this progression?
. What is the sum of the first 10 terms of this progression?
(a) (185/99)
(b) (99/185)
(c) (135/70)
(d) (70/135)
Ans: (a)
The sum of the first n terms of a harmonic progression is given by Sn = a1where a1 is the first term. Substituting the given ℎnth term, we get
Example 5: The sum of the first n terms of a harmonic progression is given by 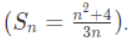 What is the common difference between the terms of this progression?
What is the common difference between the terms of this progression?
(a) (1/3)
(b) (2/3)
(c) (3/4)
(d) (4/5)
Ans: (a)
The sum of the first n terms of a harmonic progression is given bywhere a is the common difference. Comparing this with the given formula, we have
|
315 videos|182 docs|185 tests
|
FAQs on Important Formulas: Harmonic Progressions - Quantitative Aptitude for SSC CGL
| 1. What is the definition of a Harmonic Progression (HP)? |  |
| 2. What are the key formulas for Harmonic Progression? |  |
| 3. How do you convert an Arithmetic Progression (AP) to a Harmonic Progression (HP)? |  |
| 4. Can you provide an example of a Harmonic Progression? |  |
| 5. What is the relationship between Harmonic Progression and the Mean of its terms? |  |