Important Derivations: Oscillations | Physics for Grade 12 PDF Download

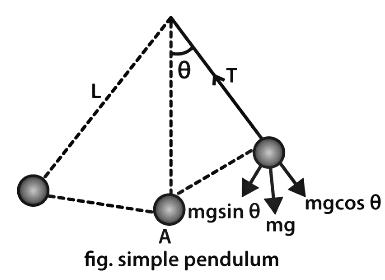
A simple pendulum can be described as a device where its point mass is attached to a light inextensible string and suspended from a fixed support. The vertical line passing through the fixed support is the mean position of a simple pendulum. The vertical distance between the point of suspension and the centre of mass of the suspended body, when it is in the mean position, is called the length of the simple pendulum, denoted by L. This form of the pendulum is based on the resonant system having a single resonant frequency.

Simple Pendulum Definition

• A simple pendulum is a mechanical arrangement that demonstrates periodic motion. The simple pendulum comprises a small bob of mass ‘m’ suspended by a thin string secured to a platform at its upper end of length L.
• The simple pendulum is a mechanical system that sways or moves in an oscillatory motion. This motion occurs in a vertical plane and is mainly driven by gravitational force. Interestingly, the bob that is suspended at the end of a thread is very light; somewhat, we can say it is even massless. The period of a simple pendulum can be made extended by increasing the length string while taking the measurements from the point of suspension to the middle of the bob. However, it should be noted that if the mass of the bob is changed, the period will remain unchanged. The period is influenced mainly by the position of the pendulum in relation to Earth, as the strength of the gravitational field is not uniform everywhere.
• In addition, pendulums are a common system whose usage is seen in various instances. Some are used in clocks to keep track of the time, while some are just used for fun in case of a child’s swing. In some cases, it is used in an unconventional manner, such as a sinker on a fishing line. In any case, we will explore and learn more about the simple pendulum on this page. We will discover the conditions under which it performs simple harmonic motion as well as derive an interesting expression for its period.

• The oscillatory motion of a simple pendulum: Oscillatory motion is defined as the to and fro motion of the pendulum in a periodic fashion, and the centre point of oscillation is known as the equilibrium position.
• The time period of a simple pendulum: It is defined as the time taken by the pendulum to finish one full oscillation and is denoted by “T”.
• The amplitude of a simple pendulum: It is defined as the distance travelled by the pendulum from the equilibrium position to one side.
• Length of a simple pendulum: It is defined as the distance between the point of suspension to the centre of the bob and is denoted by “l”.

A point mass M is suspended from the end of a light inextensible string, whose upper end is fixed to a rigid support. The mass is displaced from its mean position.

Assumptions:

• There is negligible friction from the air and the system
• The arm of the pendulum does not bend or compress and is massless
• The pendulum swings in a perfect plane
• Gravity remains constant

Time Period of Simple Pendulum Derivation

Using the equation of motion, T – mg cosθ = mv²L
The torque tends to bring the mass to its equilibrium position,
τ = mgL × sinθ = mgsinθ × L = I × α
For small angles of oscillations sin θ ≈ θ,
Therefore, Iα = -mgLθ
α = -(mgLθ)/I
– ω₀² θ = -(mgLθ)/I
ω₀² = (mgL)/I
ω₀ = √(mgL/I)
Using I = ML², [where I denote the moment of inertia of bob]
we get, ω₀ = √(g/L)
Therefore, the time period of a simple pendulum is given by,
T = 2π/ω₀ = 2π × √(L/g)

Potential Energy

The potential energy is given by the basic equation
Potential energy = mgh
m is the mass of the object
g is the acceleration due to gravity
h is the height of the object
However, the movement of the pendulum is not free fall; it is constrained by the rod or string. The height is written in terms of angle θ and length L. Thus, h = L(1 – cos θ)
When θ = 90⁰, the pendulum is at the highest point. Then cos 90⁰  = 0, and h = L.
Therefore,
Potential Energy = mgL
When θ = 0⁰, the pendulum is at the lowest point. Then, cos 0⁰ = 1. Therefore  h = L (1-1) = 0
Potential energy = mgL (1-1)  = 0
At all the points in between the potential energy is given as mgL (1 – cos θ).

Kinetic Energy 

The kinetic energy of the pendulum is given as K.E = (1/2) mv²
m is the mass of the pendulum
v is the velocity of the pendulum
At the highest point, the kinetic energy is zero, and it is maximum at the lowest point. However, the total energy as a function of time is constant.

Mechanical Energy of the Bob

In a simple pendulum, the mechanical energy of the simple pendulum is conserved.
E = KE + PE= 1/2 mv² + mgL (1 – cos θ) = constant
⇒ Note:

• If the temperature of a system changes, then the time period of the simple pendulum changes due to a change in the length of the pendulum.
• A simple pendulum is placed in a non-inertial frame of reference (accelerated lift, horizontally accelerated vehicle, vehicle moving along an inclined plane).

The mean position of the pendulum may change. In these cases, g is replaced by “g _effective” for determining the time period (T).
For example,

• A lift moving upwards with acceleration ‘a’, then, T = 2π × √(L/g_eff) = 2π √[L/(g + a)]
• If the lift is moving downward with acceleration ‘a’, then T = 2π × √(L/g_eff) = 2π √[L/(g – a)]
• For a simple pendulum of length L is equal to the radius of the earth ‘R’, L = R = 6.4 x 10⁶ m, then the time period T = 2π √R/2g
• For infinitely long pendulum L > > R near the earth surface, T = 2π × √(R/g)

A simple pendulum is an idealised model. It is not achievable in reality. But the physical pendulum is a real pendulum in which a body of finite shape oscillates. From its frequency of oscillation, we can calculate the moment of inertia of the body about the axis of rotation.

Consider a body of irregular shape and mass (m) that is free to oscillate in a vertical plane about a horizontal axis passing through a point, and weight mg acts downward at the centre of gravity (G). 
If the body is displaced through a small angle (θ) and released from this position, a torque is exerted by the weight of the body to restore its equilibrium.
τ = -mg × (d sinθ)
τ = I α
I α = – mgdsinθ
I . d²θ/dt² = – mgdsinθ
Where I = moment of inertia of a body about the axis of rotation.
d²θ/dt² = (mgd/I) θ [Since, sinθ ≈ θ]
ω₀ = √[mgd/I].

Time Period of Physical Pendulum