Solved Examples: Data Sufficiency | Data Insights for GMAT PDF Download

Solved Examples

Example 1: Coordinate Geometry

If line d in the coordinate plane has the equation y=mx+b, where m and b are constants, what is the slope of line d?
Statement 1: Line d intersects the line with equation y=6x+2 at the point (1, 8).
Statement 2: Line d is parallel to the line with equation y=(2–m)x+b–4.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (b)
Explanation: Note that the slope of a line with equation y = mx + b ism.
Statement 1: A line passing through the point (1, 8) can have any value for its slope, so it is impossible to determine the slope of line d.
For example, the line y = x + 7 intersects y = 6x + 2 at (1, 8) with a slope of 1, while the line y = 2x + 6 intersects y = 6x + 2 at (1, 8) with a slope of 2; NOT sufficient.
Statement 2: Parallel lines have the same slope, and it is possible to solve for the slope as m = 2 – m, 2m = 2, and m = 1; SUFFICIENT.

Example 2: Descriptive Statistics

A supermarket display of canned corn is shaped like a pyramid with one can on top and two more cans in each row below. If the display is only one can deep for the entire pyramid, what is the median number of cans in a row in the pyramid?
Statement 1: There are 100 cans in the pyramid.
Statement 2: The range of cans per row is 18.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(d) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (d)
Explanation: Remember that if there is a constant difference in terms that the average for the sequence = median of the sequence.
The formula for average is sum divided by the number of terms, so in this case the total number of cans = median × number of rows.
And the total number of cans = x + (x + 2) + (x + 4) … up to the total number of rows.
Therefore, two equations are already theoretically known, and only one additional equation is needed to solve for all of the values involved.
(1) If 100 is the total number of cans, then it would be possible to count from 1 + 3 + 5 + 7… to determine the total number of rows, and thereby the median, without completing the process; SUFFICIENT.
(1) If the range in cans per row is 18, then it would be possible to determine that the number of cans in the last row is 19 and from there the median, without completing the process; SUFFICIENT
The correct answer is D; each statement alone is sufficient.

Example 3: Plane Geometry

The Embeyay Expressway and Emefay Expressway intersect at a perpendicular junction coming from Ulster City and Finster Town, respectively, while a direct road connecting the two municipalities is entirely straight. How much further would a motorist traveling the expressways between Ulster City to Finster Town have to drive in comparison to another motorist who used the direct road?
Statement 1: The distance from Ulster City to the Embeyay Expressway and Emefay Expressway junction is 12 kilometers.
Statement 2: The distance from Ulster City to Finster Town on the direct road is 15 kilometers.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (c)
Explanation: Recognize that a right triangle can be formed with the junction creating the 90° angle and the two municipalities at the other two vertices.
Therefore, only two of the distances between the locations will be necessary to find the third by way of the Pythagorean Theorem.
Statement 1: This provides the distance for one of the two legs of the right triangle only; NOT sufficient.
Statement 2: This provides the distance for the hypotenuse of the right triangle only; NOT sufficient.
(Together) Complete the theorem as 12² + b² = 15² to find that the shorter leg distance is 9. From there, 12 + 9 = 21 is 6 kilometers further than 15 kilometers; SUFFICIENT.

Example 4: Inequalities

At Rounders Grocer, orange slices cost $2 a pound, pineapple chunks cost $3 a pound, and cut watermelon cost $5 a pound. If Sally buys enough of these three fruits from Rounders to make five pounds of fruit salad, and at least one pound of each, which fruit did she buy the most of by weight?
Statement 1: Sally spent less than $5 on orange slices.
Statement 2: Sally spent more than $18 on her fruit salad.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (b)
Explanation: First note that Sally must buy at least one pound of each of the fruits, which would result in a sum fixed cost of $10.
Statement 1: If Sally spent less than $5 on orange slices, then she spent must have spent more on one of the other two fruits, but it is unclear which; NOT sufficient
Statement 2: If Sally spent more than $18 then she must spend more than $8 on the two-variable pounds of fruit, which could only be accomplished by buying two more pounds of cut watermelon; Sufficient
The correct answer is B; statement 2 alone is sufficient.

Example 5: 3D Geometry (Data Sufficiency)

A cylindrical layer cake has two vanilla layers surrounding a marzipan layer, represented by the shaded region, as shown below. Is the cake split into three layers of equal volume?
Statement 1: The height of marzipan layer is equal to the radius of the whole cake.
Statement 2: The volume of the entire cake is 81π cubic inches.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (e)
Explanation: Note that the volume for a cylinder can be found from the formula πr² × height where r = radius and the height is perpendicular to the radius.
Statement 1: That the height for the marzipan layer is equal to the radius of the cake means that the volume of the marzipan layer can be found from the simplified formula πr³, but the total cake volume remains dependent on the actual height of the cake; NOT sufficient.
Statement 2: Represent the information algebraically as πr² × height = 81, but no information is provided about the height in relation to the radius; NOT sufficient.
(Together) The information together still does not relate the height to the radius.
For instance the radius could be 3 and the ratio of the marzipan layer to the others could be equal as each would have a volume of 27π.
Alternatively, the radius could = 1 and the marzipan layer would be significantly smaller than the other two layers.
The correct answer is E; both statements together are still not sufficient.

Example 6: Exponents & Radicals (Data Sufficiency)

The amount of bacteria in a culture after some t hours is given by the function f(t)=pekt where p is a constant. What is the number of bacteria after 8 hours?
Statement 1: There were approximately 275 bacteria after 2 hours
Statement 2: k = 0.16
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (c)
Explanation: Statement 1: From the function, f(t) = pe^kt, when t = 2, f(t) = 275. The equation becomes pe^2k = 275. This is one equation in two unknowns, hence, we cannot solve it. More information is required; NOT SUFFICIENT.
Statement 2: When k = 0.16, we have f(t) = pe^0.16t. In this case, p is unknown, hence more information is required; NOT SUFFICIENT.
Considering the two cases, we have pe^2k = 275 and f(t) = pe^0.16t which reduced to pe^2(0.16) = 275. We solve the equation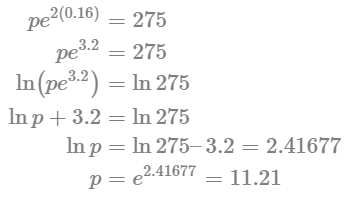

We now solve the equation
When t = 8, we have
f(8) = 11.21e^0.16(8) = 11.21e^1.28 = 40.32
The correct answer is C; BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.

Example 7: Percentages (Data Sufficiency)

If the number of rabbits at a certain pet store is 250 percent greater than the number of hamsters at the same store, how many hamsters are in the store?
Statement 1: There are 40 rabbits in the store.
Statement 2: There are 56 hamsters and rabbits in the store.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (d)
Explanation: Statement 1: Let h be the number of hamsters at the store and r be the number of rabbits to derive the equation 40 = 2.5h from the statement and given conditions, so h = 16; SUFFICIENT.
Statement 2: Using the same variables derive the equation 56 = 2.5h + h, so that h = 16; SUFFICIENT.
The correct answer is D; each statement alone is sufficient.

Example 8: Number Properties

Chiku received a $3.50 per hour raise this week. If last week she worked 40 hours per week at her old pay rate, how many fewer hours can she work this week and still guarantee that she makes more this week than she did last week?
Statement 1: She made $620 last week.
Statement 2: Her raise was 20 percent greater than that of any of her coworkers.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (a)
Explanation: Statement 1: If Chiku made $620 last week, it is possible to solve for her old pay rate, then her new pay rate, and then the number of hours she’d need to work to guarantee she makes more this week than she did last week; SUFFICIENT.
Statement 2: That her raise was greater than that of any of her coworkers introduces a new unknown variable; NOT sufficient.
The correct answer is A; statement 1 alone is sufficient.

Example 9: Division & Factoring

When integer y is divided by 2, is the remainder 1?
Statement 1: (−1)^(y+2) = −1
Statement 2: y is prime.
(a) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
(b) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
(c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(d) EACH statement ALONE is sufficient.
(e) Statements (1) and (2) TOGETHER are not sufficient.
Ans: (a)
Explanation: Statement 1: That (–1)^(y+2) = −1, dictates that y + 2 must be odd and therefore y is odd since only an odd exponent can produce a value < 0. Furthermore, if an odd number is divided by 2, the remainder must be 1; SUFFICIENT.
Statement 2: That y is prime does not definitively identify y as definitively even or odd, so the remainder could be either 0 or 1; NOT SUFFICIENT.
The correct answer is A; statement 1 alone is sufficient.