Equations of motion of kinematics describe the basic concept of the motion of an object such as the position, velocity or acceleration of an object at various times. These three equations of motion govern the motion of an object in 1D, 2D and 3D. The derivation of the equations of motion is one of the most important topics in Physics. In this article, we will show you how to derive the first, second and third equation of motion by graphical method, algebraic method and calculus method.
Class 11 Exam > Class 11 Notes > Physics Class 11 > Important Derivations: Motion in Straight Line
Important Derivations: Motion in Straight Line | Physics Class 11 PDF Download
| Table of contents |
|
| Introduction |
|
| Definition of Equations of Motion |
|
| Derivation of Equation of Motion |
|
| Derivation of First Equation of Motion |
|
Introduction
Definition of Equations of Motion
Equations of motion, in physics, are defined as equations that describe the behaviour of a physical system in terms of its motion as a function of time.
There are three equations of motion that can be used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a). The following are the three equations of motion:
- First Equation of Motion :
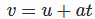
- Second Equation of Motion :
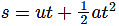
- Third Equation of Motion :
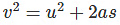
Derivation of Equation of Motion
The equations of motion can be derived using the following methods:
- Derivation of equations of motion by Simple Algebraic Method
- Derivation of equations of Motion by Graphical Method
- Derivation of equations of Motion by Calculus Method
In the next few sections, the equations of motion are derived by all the three methods in a simple and easy to understand way.
Derivation of First Equation of Motion
For the derivation, let us consider a body moving in a straight line with uniform acceleration. Then, let the initial velocity be u, acceleration is denoted as a, the time period is denoted as t, velocity is denoted as v, and the distance travelled is denoted as s.
Derivation of First Equation of Motion by Algebraic Method
We know that the acceleration of the body is defined as the rate of change of velocity.
Mathematically, acceleration is represented as follows: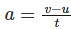
where v is the final velocity and u is the initial velocity.
Rearranging the above equation, we arrive at the first equation of motion as follows:
v = u + at
Derivation of First Equation of Motion by Graphical Method
The first equation of motion can be derived using a velocity-time graph for a moving object with an initial velocity of u, final velocity v, and acceleration a.
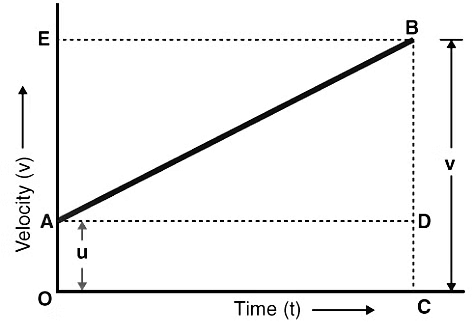
In the above graph,
- The velocity of the body changes from A to B in time t at a uniform rate.
- BC is the final velocity and OC is the total time t.
- A perpendicular is drawn from B to OC, a parallel line is drawn from A to D, and another perpendicular is drawn from B to OE (represented by dotted lines).
The following details are obtained from the graph above:
The initial velocity of the body, u = OA
The final velocity of the body, v = BC
From the graph, we know that
BC = BD + DC
Therefore, v = BD + DC
v = BD + OA (since DC = OA)
Finally,
v = BD + u (since OA = u) (Equation 1)
Now, since the slope of a velocity-time graph is equal to acceleration a.
So,
a = slope of line AB
a = BD/AD
Since AD = AC = t, the above equation becomes:
BD = at (Equation 2)
Now, combining Equation 1 & 2, the following is obtained:
v = u + at
Derivation of First Equation of Motion by Calculus Method
Since acceleration is the rate of change of velocity, it can be mathematically written as:
Rearranging the above equation, we get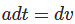
Integrating both the sides, we get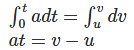
Rearranging, we get
v = u + at
Derivation of Second Equation of Motion
For the derivation of the second equation of motion, consider the same variables that were used for derivation of the first equation of motion.
Derivation of Second Equation of Motion by Algebraic Method
Velocity is defined as the rate of change of displacement. This is mathematically represented as:
Rearranging, we get
Displacement = Velocity x Time
If the velocity is not constant then in the above equation we can use average velocity in the place of velocity and rewrite the equation as follows:
Substituting the above equations with the notations used in the derivation of the first equation of motion, we get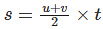
From the first equation of motion, we know that v = u + at. Putting this value of v in the above equation, we get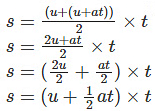
On further simplification, the equation becomes: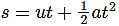
Derivation of Second Equation of Motion by Graphical Method
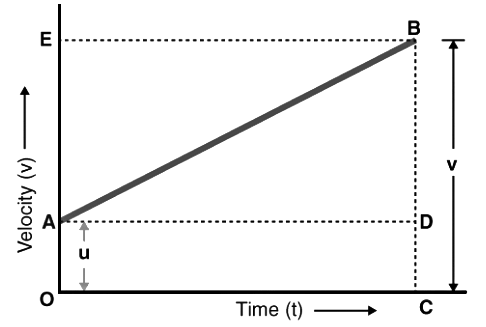
From the graph above, we can say that
Distance travelled (s) = Area of figure OABC = Area of rectangle OADC + Area of triangle ABD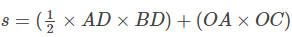
As OA=u and OC=t, the above equation becomes,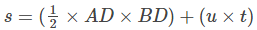 
As BD =at (from the graphical derivation of 1st equation of motion), the equation becomes,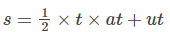 
On further simplification, the equation becomes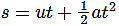
Derivation of Second Equation of Motion by Calculus Method
Velocity is the rate of change of displacement.
Mathematically, this is expressed as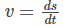
Rearranging the equation, we get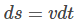 
Substituting the first equation of motion in the above equation, we get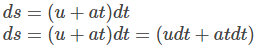 
Integrating both sides, we get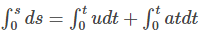 
On further simplification, the equations becomes: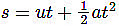 
Derivation of Third Equation of Motion
For the derivation of the third equation of motion, consider the same variables that were used for the derivation of the first and second equations of motion.
Derivation of Third Equation of Motion by Algebraic Method
We know that displacement is the product of average velocity and time. Mathematically, this can be represented as:
Substituting the standard notations, the above equation becomes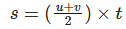
From the first equation of motion, we know that
v = u + at
Rearranging the above formula, we get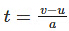
Substituting the value of t in the displacement formula, we get
Rearranging, we get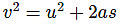
Derivation of Third Equation of Motion by Graphical Method
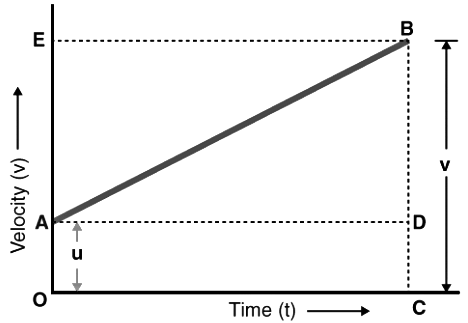
From the graph, we can say that
The total distance travelled, s is given by the Area of trapezium OABC.
Hence,
s = ½ × (Sum of Parallel Sides) × Height
s = 1/2 x (OA + CB) x OC
Since, OA = u, CB = v, and OC = t
The above equation becomes
s = 1/2 x (u+v) x t
Now, since t = (v – u)/ a
The above equation can be written as:
s = ½ x ((u+v) × (v-u))/a
Rearranging the equation, we get
s = ½ x (v+u) × (v-u)/a
s = (v2-u2)/2a
Third equation of motion is obtained by solving the above equation:
v2 = u2+2aS
Derivation of Third Equation of Motion by Calculus Method
We know that acceleration is the rate of change of velocity and can be represented as: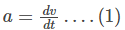
We also know that velocity is the rate of change of displacement and can be represented as: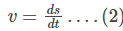
Cross multiplying (1) and (2), we get
v2 = u2 + 2as
The document Important Derivations: Motion in Straight Line | Physics Class 11 is a part of the Class 11 Course Physics Class 11.
All you need of Class 11 at this link: Class 11
|
101 videos|325 docs|100 tests
|
FAQs on Important Derivations: Motion in Straight Line - Physics Class 11
| 1. What are the equations of motion? |  |
Ans. The equations of motion are mathematical expressions that describe the relationship between an object's position, velocity, acceleration, and time. They are used to analyze the motion of objects in various scenarios.
| 2. How are the equations of motion derived? | |
Ans. The equations of motion can be derived using calculus and kinematic principles. By integrating the acceleration with respect to time, we can obtain the velocity equation, and by integrating the velocity equation with respect to time, we can obtain the displacement equation.
| 3. What is the derivation of the first equation of motion? | |
Ans. The first equation of motion, also known as the displacement equation, states that the displacement of an object is equal to its initial velocity multiplied by time, plus half the acceleration multiplied by the square of time. It can be derived by integrating the equation for velocity with respect to time.
| 4. What are some important derivations related to motion in a straight line? | |
Ans. Some important derivations related to motion in a straight line include:
- Derivation of the second equation of motion, which relates the final velocity, initial velocity, acceleration, and displacement.
- Derivation of the third equation of motion, which relates the final velocity, initial velocity, acceleration, and time.
- Derivation of the equation for average velocity, which relates the total displacement and total time.
| 5. How do the equations of motion help in solving problems related to motion? | |
Ans. The equations of motion provide a mathematical framework for analyzing and solving problems related to motion. By plugging in known values and solving for unknowns, we can determine quantities such as displacement, velocity, acceleration, and time. These equations allow us to make predictions and understand the behavior of objects in motion.
About this Document
|
4.87/5 Rating |
|
Nov 27, 2024 Last updated |
Document Description: Important Derivations: Motion in Straight Line for Class 11 2024 is part of Physics Class 11 preparation.
The notes and questions for Important Derivations: Motion in Straight Line have been prepared according to the Class 11 exam syllabus. Information about Important Derivations: Motion in Straight Line covers topics
like Introduction, Definition of Equations of Motion, Derivation of Equation of Motion, Derivation of First Equation of Motion and Important Derivations: Motion in Straight Line Example, for Class 11 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Derivations: Motion in Straight Line.
Introduction of Important Derivations: Motion in Straight Line in English is available as part of our Physics Class 11
for Class 11 & Important Derivations: Motion in Straight Line in Hindi for Physics Class 11 course.
Download more important topics related with notes, lectures and mock test series for Class 11
Exam by signing up for free. Class 11: Important Derivations: Motion in Straight Line | Physics Class 11
Description
Full syllabus notes, lecture & questions for Important Derivations: Motion in Straight Line | Physics Class 11 - Class 11 | Plus excerises question with solution to help you revise complete syllabus for Physics Class 11 | Best notes, free PDF download
Information about Important Derivations: Motion in Straight Line
In this doc you can find the meaning of Important Derivations: Motion in Straight Line defined & explained in the simplest way possible. Besides explaining types of
Important Derivations: Motion in Straight Line theory, EduRev gives you an ample number of questions to practice Important Derivations: Motion in Straight Line tests, examples and also practice Class 11
tests
|
Explore Courses for Class 11 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Summary
,mock tests for examination
,Extra Questions
,video lectures
,study material
,Objective type Questions
,Important Derivations: Motion in Straight Line | Physics Class 11
,past year papers
,Exam
,Free
,Previous Year Questions with Solutions
,ppt
,Important Derivations: Motion in Straight Line | Physics Class 11
,Important questions
,Sample Paper
,shortcuts and tricks
,Semester Notes
,Important Derivations: Motion in Straight Line | Physics Class 11
,practice quizzes
,Viva Questions
,MCQs
;
Additional Information about Important Derivations: Motion in Straight Line for Class 11 Preparation
Important Derivations: Motion in Straight Line Free PDF Download
The Important Derivations: Motion in Straight Line is an invaluable resource that delves deep into the core of the Class 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Derivations: Motion in Straight Line now and kickstart your journey towards success in the Class 11 exam.
Importance of Important Derivations: Motion in Straight Line
The importance of Important Derivations: Motion in Straight Line cannot be overstated, especially for Class 11 aspirants.
This document holds the key to success in the Class 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Derivations: Motion in Straight Line Notes
Important Derivations: Motion in Straight Line Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Derivations: Motion in Straight Line.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Derivations: Motion in Straight Line Notes on EduRev are your ultimate resource for success.
Important Derivations: Motion in Straight Line Class 11 Questions
The "Important Derivations: Motion in Straight Line Class 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Derivations: Motion in Straight Line on the App
Students of Class 11 can study Important Derivations: Motion in Straight Line alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Derivations: Motion in Straight Line,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Derivations: Motion in Straight Line is prepared as per the latest Class 11 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup