Practice Questions for Divisibility and Remainders | Quantitative for GMAT PDF Download

Q1: What is the smallest integer that is multiple of 5, 7, and 20?
(a) 70
(b) 35
(c) 200
(d) 280
(e) 140
Ans: (e)
Explanation: It is the LCM of 5, 7, and 20 which is 140. The answer is E.

Q2: Which of these numbers is not divisible by 3?
(a) 339
(b) 342
(c) 552  
(d) 1111
(e) 672
Ans: (d)
Explanation: One may answer this question using a calculator and test for divisibility by 3. However we can also test for divisibilty by adding the digits and if the result is divisible by 3 then the number is divisible by 3.  
3 + 3 + 9 = 15, divisible by 3.  
3 + 4 + 2 = 9, divisible by 3.  
5 + 5 + 2 = 12, divisible by 3.  
1 + 1 + 1 + 1 = 4, not divisible by 3.  
The number 1111 is not divisible by 3 the answer is D.

Q3: What is the smallest positive 2-digit whole number divisible by 3 and such that the sum of its digits is 9?  
(a) 27
(b) 33
(c) 72
(d) 18
(e) 90
Ans: (d)
Explanation: Let xy be the whole number with x and y the two digits that make up the number. The number is divisible by 3 may be written as follows  
10 x + y = 3 k  
The sum of x and y is equal to 9.  
x + y = 9  
Solve the above equation for y  
y = 9 - x Substitute y = 9 - x in the equation 10 x + y = 3 k to obtain.  
10 x + 9 - x = 3 k  
Solve for x  
x = (k - 3) / 3  
x is a positive integer smaller than 10  
Let k = 1, 2, 3, ... and select the first value that gives x as an integer. k = 6 gives x = 1  
Find y using the equation y = 9 - x = 8  
The number we are looking for is 18 and the answer is D. It is divisible by 3 and the sum of its digits is equal to 9 and it is the smallest and positive whole number with such properties.

Q4: Let n! = 1 x 2 x 3 x……….x n for integer n> 1. If p = 1! + (2 x 2!) + (3 x 3!) + ……(10 x 10!), then p + 2 when divided by 11! Leaves remainder of
(a) 10
(b) 0
(c) 7
(d) 1
(e) 4
Ans: (d)
Explanation: If P = 1! = 1
Then P + 2 = 3, when divided by 2! remainder will be 1.
If P = 1! + 2 × 2! = 5
Then, P + 2 = 7 when divided by 3! remainder is still 1.
Hence, P = 1! + (2 × 2!) + (3 × 3!)+ ……+ (10 × 10!)
Hence, when p + 2 is divided by 11!, the remainder is 1.

Q5: The remainder, when (1523 + 2323) is divided by 19, is:
(a) 4
(b) 15
(c) 0
(d) 18
(e) 16
Ans: (c)
Explanation: aⁿ + bⁿ is always divisible by a + b when n is odd.
Therefore 15²³ + 23²³ is always divisible by 15 + 23 = 38.
As 38 is a multiple of 19, 15²³ + 23²³ is divisible by 19.
Therefore, the required remainder is 0.

Q6: What is the sum of all two-digit numbers that give a remainder of 3 when they are divided by 7?
(a) 666
(b) 676
(c) 683
(d) 777
(e) 555
Ans: (b)
Explanation: First of all, we have to identify such 2 digit numbers.
Obviously, they are 10, 17, 24, ….94
The required sum = 10 + 17 … 94.
Now this is an A.P. with a = 10, n = 13 and d = 7
Hence, the sum is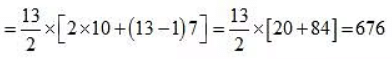


Q7: What is the remainder when 1044 × 1047 × 1050 × 1053 is divided by 33?
(a) 3
(b) 27
(c) 30
(d) 21
(e) 18
Ans: (c)
Explanation: You can solve this problem if you know this rule about remainders.
Let a number x divide the product of A and B.
The remainder will be the product of the remainders when x divides A and when x divides B.
Using this rule,
The remainder when 33 divides 1044 is 21.
The remainder when 33 divides 1047 is 24.
The remainder when 33 divides 1050 is 27.
The remainder when 33 divides 1053 is 30.
∴ the remainder when 33 divides 1044 × 1047 × 1050 × 1053 is 21 × 24 × 27 × 30.
Note: The remainder when a number is divided by a divisor 'd' will take values from 0 to (d - 1). It will not be equal to or more than 'd'
The value of 21 × 24 × 27 × 30 is more than 33.
When the value of the remainder is more than the divisor, the final remainder will be the remainder of dividing the product by the divisor.
i.e., the final remainder is the remainder when 33 divides 21 × 24 × 27 × 30.
When 33 divides 21 × 24 × 27 × 30, the remainder is 30.

Q8: If a positive integer n is divided by 5, the remainder is 3. Which of the numbers below yields a remainder of 0 when it is divided by 5?
(a) n + 3
(b) n + 2
(c) n - 1
(d) n - 2
(e) n + 1
Ans: (b)
Explanation: n divided by 5 yields a remainder equal to 3 is written as follows
n = 5 k + 3, where k is an integer.
add 2 to both sides of the above equation to obtain
n + 2 = 5 k + 5 = 5(k + 1)
The above suggests that n + 2 divided by 5 yields a remainder equal to zero. The answer is B.

Q9: If an integer n is divisible by 3, 5, and 12, what is the next larger integer divisible by all these numbers?
(a) n + 3
(b) n + 5
(c) n + 12
(d) n + 60
(e) n + 15
Ans: (d)
Explanation: If n is divisible by 3, 5 and 12 it must a multiple of the lcm of 3, 5 and 12 which is 60.
n = 60 k
n + 60 is also divisible by 60 since
n + 60 = 60 k + 60 = 60(k + 1)
The answer is D

Q10: If n is an integer, when (2n + 2)2 is divided by 4 the remainder is
(a) 0
(b) 1
(c) 2
(d) 3
(e) 4
Ans: (a)
Explanation: We first expand (2n + 2)²
(2n + 2)² = 4n² + 8n + 4
Factor 4 out.
= 4(n² + 2n + 1) (2n + 2)² is divisible by 4 and the remainder is equal to 0. The Answer is A.