Comparing Fractions | Elementary Mathematics for CDS PDF Download
Introduction
When comparing fractions, the aim is to establish which fraction is greater or lesser among two or more fractions. As fractions consist of a numerator and a denominator, specific rules are applied to ascertain their relative sizes.
How to Compare Fractions?
Comparing fractions involves a set of rules related to the numerator and the denominator. When any two fractions are compared, we get to know the greater and the smaller fraction. We need to compare fractions in our everyday lives. For example, when we need to compare the ratio of ingredients while following a recipe or to compare the scores of exams, etc. So, let us go through the different methods of comparing fractions to understand the concept better.
What is a Fraction?
Before exploring the concept of comparing fractions, let us recall fractions. A fraction is a part of a whole and it consists of two parts - the numerator and the denominator. The numerator is the number on the upper part of the fractional bar and the denominator is located below the fractional bar.
Comparing Fractions with Same Denominators
For comparing fractions with the same denominators, it becomes easier to determine the greater or the smaller fraction. After checking if the denominators are the same, we can simply look for the fraction with the bigger numerator. If both the numerators and the denominators are equal, the fractions are also equal. For example, let us compare 6/17 and 16/17
- Step 1: Observe the denominators of the given fractions: 6/17 and 16/17. The denominators are the same.
- Step 2: Now, compare the numerators. We can see that 16 > 6.
- Step 3: The fraction with the larger numerator is the larger fraction. Therefore, 6/17 < 16/17.
Comparing Fractions with Unlike Denominators
For comparing fractions with unlike denominators, we need to convert them to like denominators, for which we should find the Least Common Multiple (LCM) of the denominators. When the denominators are made the same, we can compare the fractions easily. For example, let us compare 1/2 and 2/5.
- Step 1: Observe the denominators of the given fractions: 1/2 and 2/5. They are different. So, let us find the LCM of 2 and 5. LCM(2, 5) = 10.
- Step 2: Now, let us convert them in such a way that the denominators become the same. Let us multiply the first fraction with 5/5, that is, 1/2 × 5/5 = 5/10.
- Step 3: Now, let us multiply the second fraction with 2/2 that is, 2/5 × 2/2 = 4/10.
- Step 4: Compare the fractions: 5/10 and 4/10. Since the denominators are the same, we will compare the numerators, and we can see that, 5 > 4.
- Step 5: The fraction with the larger numerator is the larger fraction, that is, 5/10 > 4/10. Therefore, 1/2 > 2/5
It should be noted that if the denominators are different and the numerators are the same, then we can easily compare fractions by looking at their denominators. The fraction with a smaller denominator has a greater value and the fraction with a larger denominator has a smaller value. For example, 2/3 > 2/6.
Decimal Method of Comparing Fractions
In this method, we compare the decimal values of fractions. For this, the numerator is divided by the denominator and the fraction is converted into a decimal. Then, the decimal values are compared. For example, let us compare 4/5 and 6/8.
- Step 1: Write 4/5 and 6/8 in decimals. 4/5 = 0.8 and 6/8 = 0.75.
- Step 2: Compare the decimal values. 0.8 > 0.75
- Step 3: The fraction with a larger decimal value would be a larger fraction. Therefore, 4/5 > 6/8.
Comparing Fractions Using Visualization
We can use various graphical methods and models to visualize larger fractions. Observe the figure given below which shows Model A and B that represent two fractions. We can easily determine that 4/8 < 4/6 because 4/6 covers a larger shaded area than 4/8. Note that the smaller fraction occupies a lesser area of the same whole. A point to be taken into consideration here is that the size of models A and B should be exactly the same for the comparison to be valid. Each model is then divided into equal parts equivalent to their respective denominators.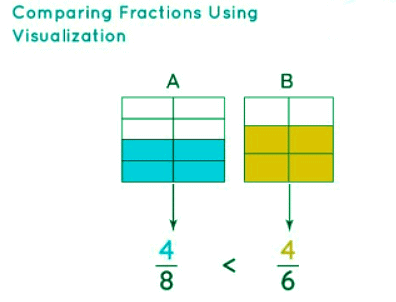
Comparing Fractions Using Cross Multiplication
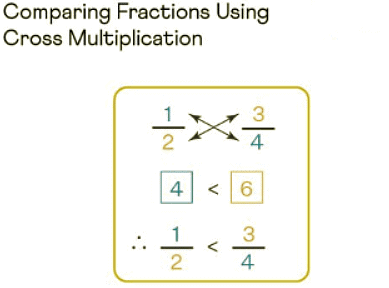
For comparing fractions using cross multiplication, we multiply the numerator of one fraction with the denominator of the other fraction. Let us understand this with the help of an example. Compare 1/2 and 3/4. Observe the figure given below which explains this better.
- Step 1: When we cross multiply the given fractions for comparing them, we need to keep in mind that if we are multiplying the numerator of the first fraction with the denominator of the second fraction, we should write the product next to the first fraction. Here, 1 × 4 = 4, and we will write 4 next to the first fraction. (Write the product on the side of the selected numerator)
- Step 2: Similarly, when we are multiplying the numerator of the second fraction with the denominator of the first fraction, we should write the product next to the second fraction. Here, 3 × 2 = 6, and we will write 6 near the second fraction.
- Step 3: Now, compare the products 4 and 6. Since 4 < 6, the respective fractions can be easily compared, that is, 1/2 < 3/4. Therefore, 1/2 < 3/4.
Solved Examples
Example 1: Compare the fractions 5/8 and 7/12.
Ans: For comparing fractions with different denominators, we need to find the LCM of the denominators. The LCM of 8 and 12 is 24. So, let us multiply 5/8 with 3/3, that is, 5/8 × 3/3 = 15/24. Now, let us multiply 7/12 with 2/2, that is, 14/24. Now that we have like fractions 15/24 and 14/24, we can easily compare them. Since 15 > 14, 5/8 > 7/12. Therefore, 5/8 > 7/12.
Example 2: Why is 5/11 > 4/11? Can you explain?
Ans: Comparing fractions becomes easier if the denominators are the same. 5/11 and 4/11 have the same denominators; hence, we can simply compare the fractions by observing the numerators. The fraction with a larger numerator will be the larger fraction. 5 > 4. Therefore, 5/11 > 4/11.
Example 3: Ryan was asked to prove that the given fractions: 4/6 and 6/9 are equal. Can you prove this using the LCM method?
Ans: We can make the denominators the same by finding the LCM of the denominators of the given fractions. The LCM of 6 and 9 is 18. So, we will multiply 4/6 with 3/3, (4/6) × (3/3) = 12/18, and 6/9 with 2/2, (6/9) × (2/2) = 12/18, which will convert them to like fractions with the same denominators. The new fractions with the same denominators will be 12/18 and 12/18. Hence, both the fractions are equal: 4/6 = 6/9. Therefore, 4/6 = 6/9.
|
165 videos|95 docs|127 tests
|
FAQs on Comparing Fractions - Elementary Mathematics for CDS
| 1. How can I compare fractions with the same denominators? |  |
| 2. How do I compare fractions with unlike denominators? |  |
| 3. Can I compare fractions using decimals? |  |
| 4. How can I visually compare fractions? |  |
| 5. What is cross multiplication and how does it help in comparing fractions? |  |

|
Explore Courses for CDS exam
|

|

















