Critical Phenomena | Chemistry Optional Notes for UPSC PDF Download
Introduction
The compressibility factor is a correction coefficient that describes the deviation of a real gas from ideal gas behaviour. It is usually represented with the symbol z, and is calculated as: (11.3.1)
(11.3.1)
It is evident from Equation 11.3.1 that the compressibility factor is dependent on the pressure, and for an ideal gas z = 1 always. For a non-ideal gas at any given pressure, z can be higher or lower than one, separating the behavior of non-ideal gases into two possibilities. The dependence of the compressibility factor against pressure is represented for H2 and CO2 in Figure 11.3.5.
 Figure 11.3.1: Non-Ideal Gases Behaviors.
Figure 11.3.1: Non-Ideal Gases Behaviors.
The two types of possible behaviors are differentiated based on the compressibility factor at P→ 0. To analyze these situations we can use the vdW equation to calculate the compressibility factor as: (11.3.2)
(11.3.2)
and then we can differentiate this equation at constant temperature with respect to changes in the pressure near P = 0, to obtain: (11.3.3)
(11.3.3)
which is then interpreted as follows:
- Type I gases:
 molecular size dominates (H2− like behavior).
molecular size dominates (H2− like behavior). - Type II gases:
 attractive forces dominates (CO2−like behavior).
attractive forces dominates (CO2−like behavior).
The dependence of the compressibility factor as a function of temperature (Figure 11.3.6) results in different plots for each of the two types of behavior.
 Figure 11.3.2: Temperature Dependence of the Compressibility Factor.
Figure 11.3.2: Temperature Dependence of the Compressibility Factor.
Both type I and type II non-ideal gases will approach the ideal gas behavior as T → ∞, because 1/RT → 0 as T → ∞. For type II gases, there are three interesting situations:
- At low T:
 which is the behavior described above.
which is the behavior described above. - At high T:
 which is the same behavior of type I gases.
which is the same behavior of type I gases. - At a very specific temperature, inversion will occur (i.e., at T=713K for CO2). This temperature is called the Boyle temperature, TB, and is the temperature at which the attractive and repulsive forces balance out. It can be calculated from the vdW equation, since
 At the Boyle’s temperature a type II gas shows ideal gas behavior over a large range of pressure.
At the Boyle’s temperature a type II gas shows ideal gas behavior over a large range of pressure.
Phase diagram of a non-ideal gas
Let’s now turn our attention to the PV phase diagram of a non-ideal gas, reported in Figure 11.3.7. Figure 11.3.3: The Pressure–Volume Diagram of a Non-Ideal Gas.
Figure 11.3.3: The Pressure–Volume Diagram of a Non-Ideal Gas.
We can start the analysis from an isotherm at a high temperature. Since every gas will behave as an ideal gas at those conditions, the corresponding isotherms will look similar to those of an ideal gas (T5 and T4 in Figure 11.3.3). Lowering the temperature, we start to see the deviation from ideality getting more prominent ( T3 in Figure 11.3.3) until we reach a particular temperature called the critical temperature, Tc.
Definition: Critical Temperature
The temperature above which no appearance of a second phase is observed, regardless of how high the pressure becomes. At the critical temperature and below, the gas liquefies when the pressure is increased. For this reason, the liquefaction of a gas is called a critical phenomenon.
The critical temperature is the coordinate of a unique point, called the critical point, that can be visualized in the three-dimensional T, P, V diagram of each gas (Figure 11.3.4)1.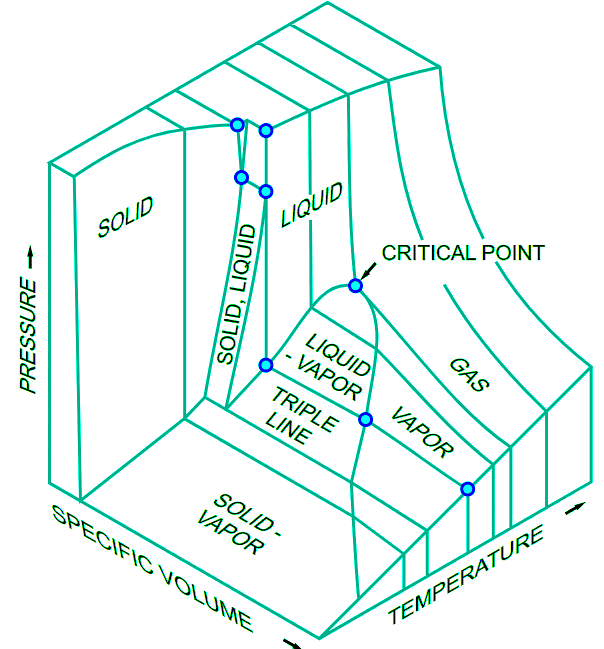 Figure 11.3.4: The three-dimensional diagram. (CC By-SA 3.0 unported; Donald L. Smith via Wikipedia)
Figure 11.3.4: The three-dimensional diagram. (CC By-SA 3.0 unported; Donald L. Smith via Wikipedia)
The critical point has coordinates  These critical coordinates can be determined from the vdW equation at Tc, as:
These critical coordinates can be determined from the vdW equation at Tc, as: (11.3.4)
(11.3.4)
These relations are used, in practice, to determine the vdW constants a, and b from the experimentally measured critical isotherms.
The critical compressibility factor, zc, is predicted from the vdW equation at: (11.3.5)
(11.3.5)
a value that is independent of the gas. Experimentally measured values of zc for different non-ideal gases are in the range of 0.2–0.3. These values can be used to infer the accuracy of the vdW equation for each non-ideal gas. Since the experimental zc is usually lower than the one calculated from the vdW equation, we can deduce that the vdW equation overestimates the critical molar volume.
FAQs on Critical Phenomena - Chemistry Optional Notes for UPSC
| 1. What is a phase diagram? |  |
| 2. What is a non-ideal gas? |  |
| 3. What are critical phenomena? |  |
| 4. How does a phase diagram of a non-ideal gas differ from that of an ideal gas? |  |
| 5. Can a non-ideal gas exhibit critical phenomena? |  |

|
Explore Courses for UPSC exam
|

|
 molecular size dominates (H2− like behavior).
molecular size dominates (H2− like behavior). attractive forces dominates (CO2−like behavior).
attractive forces dominates (CO2−like behavior). which is the behavior described above.
which is the behavior described above. which is the same behavior of type I gases.
which is the same behavior of type I gases. At the Boyle’s temperature a type II gas shows ideal gas behavior over a large range of pressure.
At the Boyle’s temperature a type II gas shows ideal gas behavior over a large range of pressure.















