Rotational Spectroscopy of Diatomic Molecules | Chemistry Optional Notes for UPSC PDF Download
Introduction
- Similar to most quantum mechanical systems our model can be completely described by its wave function. Therefore, when we attempt to solve for the energy we are lead to the Schrödinger Equation. In the context of the rigid rotor where there is a natural center (rotation around the COM) the wave functions are best described in spherical coordinates.
- In addition to having pure rotational spectra diatomic molecules have rotational spectra associated with their vibrational spectra. The order of magnitude differs greatly between the two with the rotational transitions having energy proportional to 1-10 cm-1 (microwave radiation) and the vibrational transitions having energy proportional to 100-3,000 cm-1 (infrared radiation). Rotational spectroscopy is therefore referred to as microwave spectroscopy.
Rigid Rotor Model
A diatomic molecule consists of two masses bound together. The distance between the masses, or the bond length, (l) can be considered fixed because the level of vibration in the bond is small compared to the bond length. As the molecule rotates it does so around its COM (observed in Figure 1:. as the intersection of R1 and R2) with a frequency of rotation of νrot given in radians per second.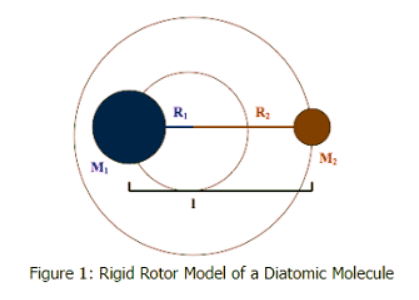
Reduced Mass
The system can be simplified using the concept of reduced mass which allows it to be treated as one rotating body. The system can be entirely described by the fixed distance between the two masses instead of their individual radii of rotation. Relationships between the radii of rotation and bond length are derived from the COM given by:
where l is the sum of the two radii of rotation:
Through simple algebra both radii can be found in terms of their masses and bond length:
and
The kinetic energy of the system, T, is sum of the kinetic energy for each mass:
where
and
Using the angular velocity,
the kinetic energy can now be written as:
With the moment of inertia,
the kinetic energy can be further simplified:
The moment of inertia can be rewritten by plugging in for R1 and R2:
where
is the reduced mass, μ. The moment of inertia and the system are now solely defined by a single mass, μ, and a single length, l:
Angular Momentum
Another important concept when dealing with rotating systems is the the angular momentum defined by: L = Iω
Looking back at the kinetic energy:
The angular momentum can now be described in terms of the moment of inertia and kinetic energy: L2 = 2IT.
Setting up the Schrödinger Equation
The wave functions for the rigid rotor model are found from solving the time-independent Schrödinger Equation:
Where the Hamiltonian Operator is:
where ∇2 is the Laplacian Operator and can be expressed in either Cartesian coordinates:
or in spherical coordinates:
At this point it is important to incorporate two assumptions:
- The distance between the two masses is fixed. This causes the terms in the Laplacian containing ∂/∂r to be zero.
- The orientation of the masses is completely described by θ and ϕ and in the absence of electric or magnetic fields the energy is independent of orientation. This causes the potential energy portion of the Hamiltonian to be zero.
The wave functions ψ(θ, ϕ) are customarily represented by Y(θ, ϕ) and are called spherical harmonics.
The Hamiltonian Operator can now be written:
with the Angular Momentum Operator being defined:
The Schrödinger Equation now expressed:
Solving the Schrödinger Equation
The Schrödinger Equation can be solved using separation of variables.
Step 1:
Set the Schrödinger Equation equal to zero:
Step 2: Because the terms containing Θ(θ) are equal to the terms containing Φ(ϕ) they must equal the same constant in order to be defined for all values:
Step 3: Solving for Φ is fairly simple and yields:
where m = 0, ±1, ±2,...
Solving for θ is considerably more complicated but gives the quantized result:
where J is the rotational level with J = 0, 1, 2,...
Step 4: The energy is quantized by expressing in terms of β:
Step 5: Using the rotational constant, B = ℏ2/2I, the energy is further simplified: E = BJ(J + 1)
Energy of Rotational Transitions
When a molecule is irradiated with photons of light it may absorb the radiation and undergo an energy transition. The energy of the transition must be equivalent to the energy of the photon of light absorbed given by: E = hν. For a diatomic molecule the energy difference between rotational levels (J to J+1) is given by:
with J = 0, 1, 2,...
Because the difference of energy between rotational levels is in the microwave region (1-10 cm-1) rotational spectroscopy is commonly called microwave spectroscopy. In spectroscopy it is customary to represent energy in wave numbers (cm-1), in this notation B is written as  To convert from units of energy to wave numbers simply divide by h and c, where c is the speed of light in cm/s (c=2.998e10 cm/s). In wave numbers
To convert from units of energy to wave numbers simply divide by h and c, where c is the speed of light in cm/s (c=2.998e10 cm/s). In wave numbers 
 Figure 2: predicts the rotational spectra of a diatomic molecule to have several peaks spaced by
Figure 2: predicts the rotational spectra of a diatomic molecule to have several peaks spaced by  This contrasts vibrational spectra which have only one fundamental peak for each vibrational mode. From the rotational spectrum of a diatomic molecule the bond length can be determined. Because
This contrasts vibrational spectra which have only one fundamental peak for each vibrational mode. From the rotational spectrum of a diatomic molecule the bond length can be determined. Because  is a function of I and therefore a function of l (bond length), so l can be readily solved for:
is a function of I and therefore a function of l (bond length), so l can be readily solved for:
Selection rules only permit transitions between consecutive rotational levels: ΔJ =J ± 1, and require the molecule to contain a permanent dipole moment. Due to the dipole requirement, molecules such as HF and HCl have pure rotational spectra and molecules such as H2 and N2 are rotationally inactive.
Centrifugal Distortion
As molecules are excited to higher rotational energies they spin at a faster rate. The faster rate of spin increases the centrifugal force pushing outward on the molecules resulting in a longer average bond length. Looking back, B and l are inversely related. Therefore the addition of centrifugal distortion at higher rotational levels decreases the spacing between rotational levels. The correction for the centrifugal distortion may be found through perturbation theory:
Rotation-Vibration Transitions
Rotational transitions are on the order of 1-10 cm-1, while vibrational transitions are on the order of 1000 cm-1. The difference of magnitude between the energy transitions allow rotational levels to be superimposed within vibrational levels.
Combining the energy of the rotational levels,  with the vibrational levels,
with the vibrational levels,
 yields the total energy of the respective rotation-vibration levels:
yields the total energy of the respective rotation-vibration levels:
Following the selection rule, ΔJ = J ± 1, Figure 3. shows all of the allowed transitions for the first three rotational states, where J" is the initial state and J' is the final state.
When the ΔJ = +1 transitions are considered (blue transitions) the initial energy is given by:  and the final energy is given by:
and the final energy is given by:

The energy of the transition,  is therefore:
is therefore:
where J"=0, 1, 2,...
When the ΔJ = −1 transitions are considered (red transitions) the initial energy is given by:  and the final energy is given by:
and the final energy is given by:
The energy of the transition is therefore: 
The difference in energy between the J + 1 transitions and J - 1 transitions causes splitting of vibrational spectra into two branches. The J - 1 transitions, shown by the red lines in Figure 3, are lower in energy than the pure vibrational transition and form the P-branch. The J + 1 transitions, shown by the blue lines in Figure 3. are higher in energy than the pure vibrational transition and form the R-branch. Notice that because the ΔJ = ±0 transition is forbidden there is no spectral line associated with the pure vibrational transition. Therefore there is a gap between the P-branch and R-branch, known as the q branch.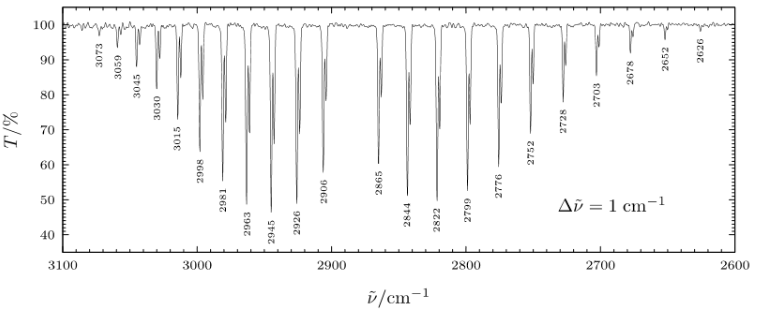
In the high resolution HCl rotation-vibration spectrum the splitting of the P-branch and R-branch is clearly visible. Due to the small spacing between rotational levels high resolution spectrophotometers are required to distinguish the rotational transitions.
Rotation-Vibration Interactions
Recall the Rigid-Rotor assumption that the bond length between two atoms in a diatomic molecule is fixed. However, the anharmonicity correction for the harmonic oscillator predicts the gaps between energy levels to decrease and the equilibrium bond length to increase as higher vibrational levels are accessed. Due to the relationship between the rotational constant and bond length:
The rotational constant is dependent on the vibrational level:
Where the anharmonicity correction and v is the vibrational level. As a consequence the spacing between rotational levels decreases at higher vibrational levels and unequal spacing between rotational levels in rotation-vibration spectra occurs.
the anharmonicity correction and v is the vibrational level. As a consequence the spacing between rotational levels decreases at higher vibrational levels and unequal spacing between rotational levels in rotation-vibration spectra occurs.
Including the rotation-vibration interaction the spectra can be predicted.
For the R-branch
where J = 0, 1, 2,...
For the P-branch
where J = 1, 2, 3,...
Because  as J increases:
as J increases:
- Spacing in the R-branch decreases.
- Spacing in the P-branch increases.
FAQs on Rotational Spectroscopy of Diatomic Molecules - Chemistry Optional Notes for UPSC
| 1. What is rotational spectroscopy? |  |
| 2. How is the Schrödinger equation used in rotational spectroscopy? |  |
| 3. What is the reduced mass in rotational spectroscopy? |  |
| 4. What are rotation-vibration transitions in rotational spectroscopy? |  |
| 5. How do rotational-vibration interactions affect rotational spectroscopy? |  |

|
Explore Courses for UPSC exam
|

|
















