The Third Law of Thermodynamics | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| The Third Law Lets us Calculate Absolute Entropies |

|
| Calculating ΔSsys |

|
| Solved Example |

|
Introduction
- The atoms, molecules, or ions that compose a chemical system can undergo several types of molecular motion, including translation, rotation, and vibration (Figure 13.6.1). The greater the molecular motion of a system, the greater the number of possible microstates and the higher the entropy. A perfectly ordered system with only a single microstate available to it would have an entropy of zero. The only system that meets this criterion is a perfect crystal at a temperature of absolute zero (0 K), in which each component atom, molecule, or ion is fixed in place within a crystal lattice and exhibits no motion (ignoring quantum zero point motion).
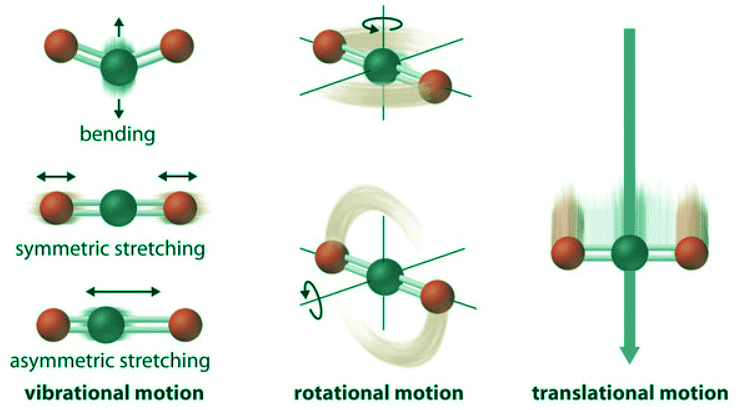
Figure 13.6.1: Molecular Motions. Vibrational, rotational, and translational motions of a carbon dioxide molecule are illustrated here. Only a perfectly ordered, crystalline substance at absolute zero would exhibit no molecular motion (classically; there will always be motion quantum mechanically) and have zero entropy. In practice, this is an unattainable ideal.
- This system may be described by a single microstate, as its purity, perfect crystallinity and complete lack of motion (at least classically, quantum mechanics argues for constant motion) means there is but one possible location for each identical atom or molecule comprising the crystal (Ω=1). According to the Boltzmann equation, the entropy of this system is zero.
S = k ln Ω
= k ln (1)
= 0 - In practice, absolute zero is an ideal temperature that is unobtainable, and a perfect single crystal is also an ideal that cannot be achieved. Nonetheless, the combination of these two ideals constitutes the basis for the third law of thermodynamics: the entropy of any perfectly ordered, crystalline substance at absolute zero is zero.
Definition: Third Law of Thermodynamics
The entropy of a pure, perfect crystalline substance at 0 K is zero.
- The third law of thermodynamics has two important consequences: it defines the sign of the entropy of any substance at temperatures above absolute zero as positive, and it provides a fixed reference point that allows us to measure the absolute entropy of any substance at any temperature. In this section, we examine two different ways to calculate ΔS for a reaction or a physical change.
- The first, based on the definition of absolute entropy provided by the third law of thermodynamics, uses tabulated values of absolute entropies of substances. The second, based on the fact that entropy is a state function, uses a thermodynamic cycle similar to those discussed previously.
Standard-State Entropies
One way of calculating ΔS for a reaction is to use tabulated values of the standard molar entropy (So), which is the entropy of 1 mol of a substance under standard pressure (1 bar). Often the standard molar entropy is given at 298 K and is often demarked as ΔSo298. The units of So are J/(mol•K). Unlike enthalpy or internal energy, it is possible to obtain absolute entropy values by measuring the entropy change that occurs between the reference point of 0 K (corresponding to S=0) and 298 K (Tables T1 and T2).
As shown in Table 13.6.1, for substances with approximately the same molar mass and number of atoms, So values fall in the order
So(gas) ≫ So(liquid) > So(solid). (13.6.1)
For instance, So for liquid water is 70.0 J/(mol•K), whereas So for water vapor is 188.8 J/(mol•K). Likewise, So is 260.7 J/(mol•K) for gaseous I2 and 116.1 J/(mol•K) for solid I2. This order makes qualitative sense based on the kinds and extents of motion available to atoms and molecules in the three phases (Figure 13.6.1). The correlation between physical state and absolute entropy is illustrated in Figure 13.6.2, which is a generalized plot of the entropy of a substance versus temperature.
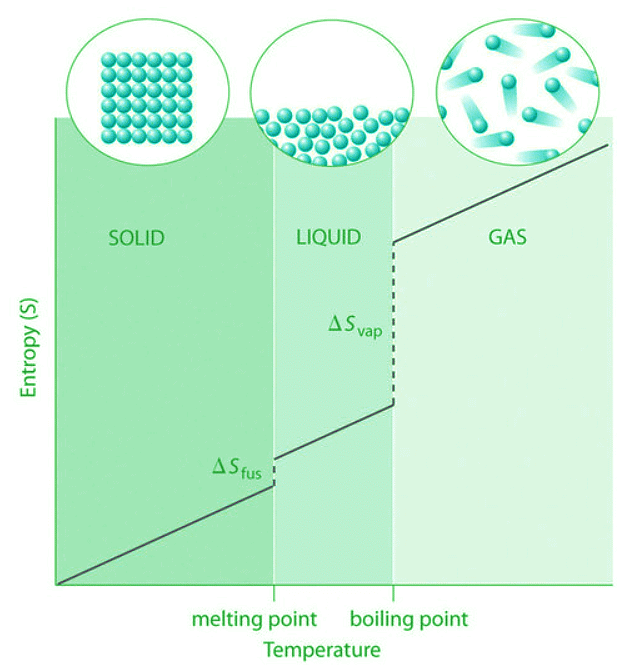
Figure 13.6.2: A Generalized Plot of Entropy versus Temperature for a Single Substance. Absolute entropy increases steadily with increasing temperature until the melting point is reached, where it jumps suddenly as the substance undergoes a phase change from a highly ordered solid to a disordered liquid (ΔSfus). The entropy again increases steadily with increasing temperature until the boiling point is reached, where it jumps suddenly as the liquid undergoes a phase change to a highly disordered gas.
The Third Law Lets us Calculate Absolute Entropies
The absolute entropy of a substance at any temperature above 0 K must be determined by calculating the increments of heat q required to bring the substance from 0 K to the temperature of interest, and then summing the ratios q/T . Two kinds of experimental measurements are needed:
- The enthalpies associated with any phase changes the substance may undergo within the temperature range of interest. Melting of a solid and vaporization of a liquid correspond to sizeable increases in the number of microstates available to accept thermal energy, so as these processes occur, energy will flow into a system, filling these new microstates to the extent required to maintain a constant temperature (the freezing or boiling point); these inflows of thermal energy correspond to the heats of fusion and vaporization. The entropy increase associated with transition at temperature T is
 (13.6.2)
(13.6.2) - The heat capacity C of a phase expresses the quantity of heat required to change the temperature by a small amount ΔT, or more precisely, by an infinitesimal amount dT. Thus the entropy increase brought about by warming a substance over a range of temperatures that does not encompass a phase transition is given by the sum of the quantities C(dT/T) for each increment of temperature dT. This is of course just the integral
 (13.6.3)
(13.6.3) - Because the heat capacity is itself slightly temperature dependent, the most precise determinations of absolute entropies require that the functional dependence of C on T be used in the integral in Equation 13.6.3, i.e.,:
 (13.6.4)
(13.6.4) - When this is not known, one can take a series of heat capacity measurements over narrow temperature increments ΔT and measure the area under each section of the curve. The area under each section of the plot represents the entropy change associated with heating the substance through an interval ΔT. To this must be added the enthalpies of melting, vaporization, and of any solid-solid phase changes.
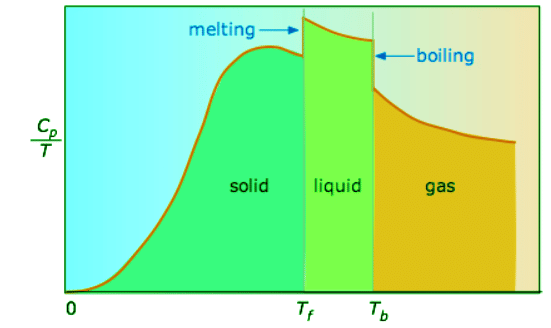
Figure 13.6.3: Heat capacity/temperature as a function of temperature. (CC BY; Stephan Lower)
Values of Cp for temperatures near zero are not measured directly, but can be estimated from quantum theory. The cumulative areas from 0 K to any given temperature (Figure 13.6.3) are then plotted as a function of T , and any phase-change entropies such as
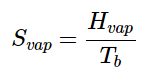 (13.6.5)
(13.6.5)
are added to obtain the absolute entropy at temperature T. As shown in Figure 13.6.2 above, the entropy of a substance increases with temperature, and it does so for two reasons:
- As the temperature rises, more microstates become accessible, allowing thermal energy to be more widely dispersed. This is reflected in the gradual increase of entropy with temperature.
- The molecules of solids, liquids, and gases have increasingly greater freedom to move around, facilitating the spreading and sharing of thermal energy. Phase changes are therefore accompanied by massive and discontinuous increase in the entropy.
[Question: 950628]
Calculating ΔSsys
We can make careful calorimetric measurements to determine the temperature dependence of a substance’s entropy and to derive absolute entropy values under specific conditions. Standard entropies are given the label So298 for values determined for one mole of substance at a pressure of 1 bar and a temperature of 298 K. The standard entropy change (ΔSo) for any process may be computed from the standard entropies of its reactant and product species like the following: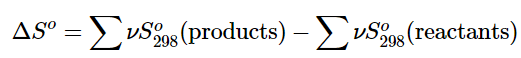 (13.6.6)
(13.6.6)
Here, ν represents stoichiometric coefficients in the balanced equation representing the process. For example, ΔSo for the following reaction at room temperature
mA + nB ⟶ xC + yD (13.6.7)
is computed as the following:
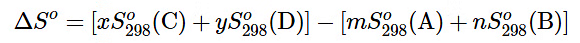 (13.6.8)
(13.6.8)
Table 13.6.1 lists some standard entropies at 298.15 K. You can find additional standard entropies in Tables T1 and T2
Table 13.6.1: Standard Molar Entropy Values of Selected Substances at 25°C
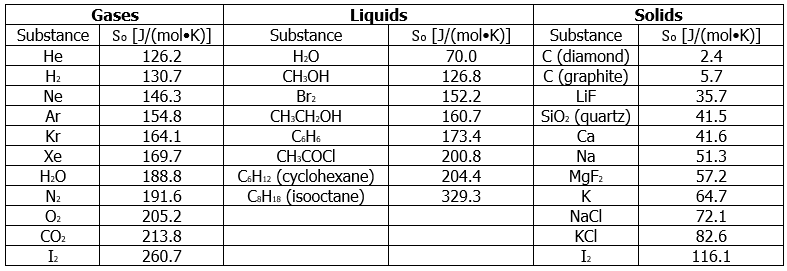
A closer examination of Table 13.6.1 also reveals that substances with similar molecular structures tend to have similar So values. Among crystalline materials, those with the lowest entropies tend to be rigid crystals composed of small atoms linked by strong, highly directional bonds, such as diamond (So = 2.4J/(mol∙K). In contrast, graphite, the softer, less rigid allotrope of carbon, has a higher So (5.7 J/(mol•K)) due to more disorder (microstates) in the crystal. Soft crystalline substances and those with larger atoms tend to have higher entropies because of increased molecular motion and disorder. Similarly, the absolute entropy of a substance tends to increase with increasing molecular complexity because the number of available microstates increases with molecular complexity. For example, compare the So values for CH3OH(l) and CH3CH2OH(l). Finally, substances with strong hydrogen bonds have lower values of So, which reflects a more ordered structure.
Entropy increases with softer, less rigid solids, solids that contain larger atoms, and solids with complex molecular structures.
To calculate ΔSo for a chemical reaction from standard molar entropies, we use the familiar “products minus reactants” rule, in which the absolute entropy of each reactant and product is multiplied by its stoichiometric coefficient in the balanced chemical equation. Example 13.6.1 illustrates this procedure for the combustion of the liquid hydrocarbon isooctane (C8H18; 2,2,4-trimethylpentane).
Solved Example
Example 1: Use the data in Table 13.6.1 to calculate ΔSo for the reaction of liquid isooctane with O2(g) to give CO2(g) and H2O(g) at 298 K.
Given: standard molar entropies, reactants, and products
Asked for: ΔS°
Strategy: Write the balanced chemical equation for the reaction and identify the appropriate quantities in Table 13.6.1. Subtract the sum of the absolute entropies of the reactants from the sum of the absolute entropies of the products, each multiplied by their appropriate stoichiometric coefficients, to obtain ΔSo for the reaction.
Ans: The balanced chemical equation for the complete combustion of isooctane (C8H18) is as follows:
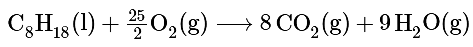
We calculate ΔSo for the reaction using the “products minus reactants” rule, where m and n are the stoichiometric coefficients of each product and each reactant: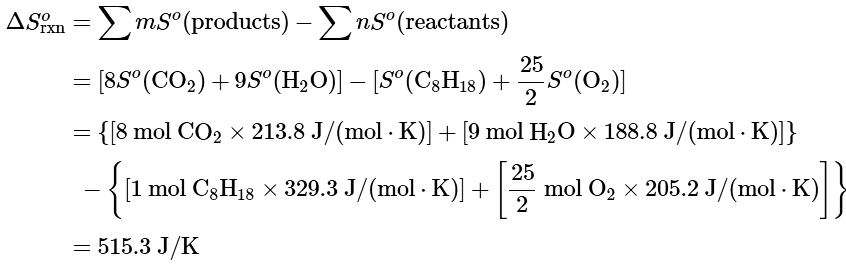
ΔSo is positive, as expected for a combustion reaction in which one large hydrocarbon molecule is converted to many molecules of gaseous products.
Example 2: Calculate the standard entropy change for the following process at 298 K:
H2O(g) ⟶ H2O(l)
Ans: The value of the standard entropy change at room temperature, ΔSo298, is the difference between the standard entropy of the product, H2O(l), and the standard entropy of the reactant, H2O(g).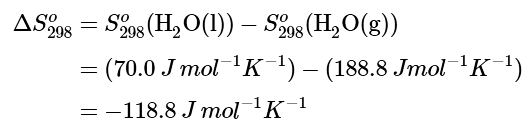
The value for ΔSo298 is negative, as expected for this phase transition (condensation), which the previous section discussed.
Summary
- Energy values, as you know, are all relative, and must be defined on a scale that is completely arbitrary; there is no such thing as the absolute energy of a substance, so we can arbitrarily define the enthalpy or internal energy of an element in its most stable form at 298 K and 1 atm pressure as zero. The same is not true of the entropy; since entropy is a measure of the “dilution” of thermal energy, it follows that the less thermal energy available to spread through a system (that is, the lower the temperature), the smaller will be its entropy. In other words, as the absolute temperature of a substance approaches zero, so does its entropy. This principle is the basis of the Third law of thermodynamics, which states that the entropy of a perfectly-ordered solid at 0 K is zero.
- In practice, chemists determine the absolute entropy of a substance by measuring the molar heat capacity (Cp) as a function of temperature and then plotting the quantity Cp/T versus T. The area under the curve between 0 K and any temperature T is the absolute entropy of the substance at T. In contrast, other thermodynamic properties, such as internal energy and enthalpy, can be evaluated in only relative terms, not absolute terms.
- The second law of thermodynamics states that a spontaneous process increases the entropy of the universe, Suniv > 0. If ΔSuniv < 0, the process is nonspontaneous, and if ΔSuniv = 0, the system is at equilibrium. The third law of thermodynamics establishes the zero for entropy as that of a perfect, pure crystalline solid at 0 K. With only one possible microstate, the entropy is zero. We may compute the standard entropy change for a process by using standard entropy values for the reactants and products involved in the process.
FAQs on The Third Law of Thermodynamics - Chemistry Optional Notes for UPSC
| 1. What is the Third Law of Thermodynamics? |  |
| 2. How does the Third Law of Thermodynamics help in calculating absolute entropies? |  |
| 3. What is the significance of calculating ΔSsys? |  |
| 4. Can the Third Law of Thermodynamics be applied to non-crystalline substances? |  |
| 5. How is the Third Law of Thermodynamics relevant to the UPSC exam? |  |

|
Explore Courses for UPSC exam
|

|
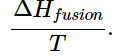 (13.6.2)
(13.6.2)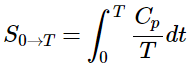 (13.6.3)
(13.6.3)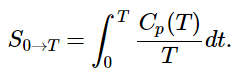 (13.6.4)
(13.6.4)















