Absorption of light & The Beer-Lambert Law | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| The Absorbance of a Solution |

|
| The Beer-Lambert Law |

|
| The Importance of Concentration |

|
| The importance of the container shape |

|
The Absorbance of a Solution
For each wavelength of light passing through the spectrometer, the intensity of the light passing through the reference cell is measured. This is usually referred to as Io - that's I for Intensity. The intensity of the light passing through the sample cell is also measured for that wavelength - given the symbol, I. If I is less than Io, then the sample has absorbed some of the light (neglecting reflection of light off the cuvette surface). A simple bit of math is then done in the computer to convert this into something called the absorbance of the sample - given the symbol, A .
The intensity of the light passing through the sample cell is also measured for that wavelength - given the symbol, I. If I is less than Io, then the sample has absorbed some of the light (neglecting reflection of light off the cuvette surface). A simple bit of math is then done in the computer to convert this into something called the absorbance of the sample - given the symbol, A .
The absorbance of a transition depends on two external assumptions:
- The absorbance is directly proportional to the concentration (c) of the solution of the sample used in the experiment.
- The absorbance is directly proportional to the length of the light path ( l ), which is equal to the width of the cuvette.
Assumption one relates the absorbance to concentration and can be expressed as
The absorbance (A) is defined via the incident intensity Io and transmitted intensity I by
Assumption two can be expressed as
Combining Equations 1 and 3:
This proportionality can be converted into an equality by including a proportionality constant (ϵ).
This formula is the common form of the Beer-Lambert Law, although it can be also written in terms of intensities:
The constant ϵ is called molar absorptivity or molar extinction coefficient and is a measure of the probability of the electronic transition. On most of the diagrams you will come across, the absorbance ranges from 0 to 1, but it can go higher than that. An absorbance of 0 at some wavelength means that no light of that particular wavelength has been absorbed. The intensities of the sample and reference beam are both the same, so the ratio Io/I is 1 and the log10 of 1 is zero.
Solved Example
Example: In a sample with an absorbance of 1 at a specific wavelength, what is the relative amount of light that was absorbed by the sample?
Ans: This question does not need Beer-Lambert Law (Equation 5) to solve, but only the definition of absorbance (Equation 2)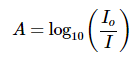
The relative loss of intensity is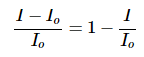
Equation 2 can be rearranged using the properties of logarithms to solved for the relative loss of intensity: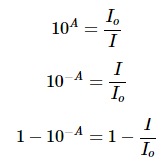
Substituting in A = 1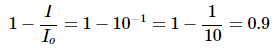
Hence 90% of the light at that wavelength has been absorbed and that the transmitted intensity is 10% of the incident intensity. To confirm, substituting these values into Equation 2 to get the absorbance back:
and
The Beer-Lambert Law
You will find that various different symbols are given for some of the terms in the equation - particularly for the concentration and the solution length.
The Greek letter epsilon in these equations is called the molar absorptivity - or sometimes the molar absorption coefficient. The larger the molar absorptivity, the more probable the electronic transition. In uv spectroscopy, the concentration of the sample solution is measured in mol L-1 and the length of the light path in cm. Thus, given that absorbance is unitless, the units of molar absorptivity are L mol-1 cm-1. However, since the units of molar absorptivity is always the above, it is customarily reported without units.
Solved Examples
Example 1: Guanosine
Guanosine has a maximum absorbance of 275 nm. ϵ275 = 8400M−1cm−1 and the path length is 1 cm. Using a spectrophotometer, you find the that A275 = 0.70. What is the concentration of guanosine?
Ans: To solve this problem, you must use Beer's Law.
A = ϵlc (9)
0.70 = (8400 M-1 cm-1)(1 cm)( c)
Next, divide both side by [(8400 M-1 cm-1)(1 cm)]
c = 8.33 x 10-5 mol/L.
Example 2: There is a substance in a solution (4 g/liter). The length of cuvette is 2 cm and only 50% of the certain light beam is transmitted. What is the extinction coefficient?
Ans: Using Beer-Lambert Law, we can compute the absorption coefficient. Thus,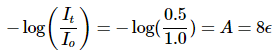
Then we obtain that
ϵ = 0.0376
Example 3: In Example 2 above, what is the molar absorption coefficient if the molecular weight is 100?
Ans: It can simply obtained by multiplying the absorption coefficient by the molecular weight.
Thus, ϵ = 0.0376 x 100 = 3.76 L·mol-1·cm-1
The Importance of Concentration
The proportion of the light absorbed will depend on how many molecules it interacts with. Suppose you have got a strongly colored organic dye. If it is in a reasonably concentrated solution, it will have a very high absorbance because there are lots of molecules to interact with the light. However, in an incredibly dilute solution, it may be very difficult to see that it is colored at all. The absorbance is going to be very low. Suppose then that you wanted to compare this dye with a different compound. Unless you took care to make allowance for the concentration, you couldn't make any sensible comparisons about which one absorbed the most light.
Solved Examples
Example 1: In Example 2 above, how much is the beam of light is transmitted when 8 g/liter?
Ans: Since we know ϵ, we can calculate the transmission using Beer-Lambert Law. Thus,
log(1) − log(It) = 0 − log(It) = 0.0376 x 8 x 2 = 0.6016
log(It) = -0.6016
Therefore, It = 0.2503 = 25%
Example 2: The absorption coefficient of a glycogen-iodine complex is 0.20 at light of 450 nm. What is the concentration when the transmission is 40 % in a cuvette of 2 cm?
Ans: It can also be solved using Beer-Lambert Law. Therefore,
−log(It) = −log10(0.4) = 0.20 × c × 2(10)
Then c = 0.9948
The importance of the container shape
Suppose this time that you had a very dilute solution of the dye in a cube-shaped container so that the light traveled 1 cm through it. The absorbance is not likely to be very high. On the other hand, suppose you passed the light through a tube 100 cm long containing the same solution. More light would be absorbed because it interacts with more molecules. Again, if you want to draw sensible comparisons between solutions, you have to allow for the length of the solution the light is passing through. Both concentration and solution length are allowed for in the Beer-Lambert Law.
Molar Absorptivity
- The Beer-Lambert law (Equation 5 ) can be rearranged to obtain an expression for ϵ (the molar absorptivity):

- Remember that the absorbance of a solution will vary as the concentration or the size of the container varies. Molar absorptivity compensates for this by dividing by both the concentration and the length of the solution that the light passes through. Essentially, it works out a value for what the absorbance would be under a standard set of conditions - the light traveling 1 cm through a solution of 1 mol dm-3. That means that you can then make comparisons between one compound and another without having to worry about the concentration or solution length.
- Values for molar absorptivity can vary hugely. For example, ethanal has two absorption peaks in its UV-visible spectrum - both in the ultra-violet. One of these corresponds to an electron being promoted from a lone pair on the oxygen into a pi anti-bonding orbital; the other from a π bonding orbital into a π anti-bonding orbital. Table 1 gives values for the molar absorptivity of a solution of ethanal in hexane. Notice that there are no units given for absorptivity. That's quite common since it assumes the length is in cm and the concentration is mol dm-3, the units are mol-1 dm3 cm-1.
Table 1
- The ethanal obviously absorbs much more strongly at 180 nm than it does at 290 nm. (Although, in fact, the 180 nm absorption peak is outside the range of most spectrometers.) You may come across diagrams of absorption spectra plotting absorptivity on the vertical axis rather than absorbance. However, if you look at the figures above and the scales that are going to be involved, you aren't really going to be able to spot the absorption at 290 nm. It will be a tiny little peak compared to the one at 180 nm. To get around this, you may also come across diagrams in which the vertical axis is plotted as log10(molar absorptivity).
- If you take the logs of the two numbers in the table, 15 becomes 1.18, while 10,000 becomes 4. That makes it possible to plot both values easily, but produces strangely squashed-looking spectra!
FAQs on Absorption of light & The Beer-Lambert Law - Chemistry Optional Notes for UPSC
| 1. What is the Beer-Lambert Law? |  |
| 2. How is the concentration of a solute related to its absorbance? |  |
| 3. Why is concentration important in the context of the Beer-Lambert Law? |  |
| 4. How does the shape of the container impact light absorption? |  |
| 5. What are the practical applications of the Beer-Lambert Law? |  |

|
Explore Courses for UPSC exam
|

|


















